ОТЧЕТ ПО МО

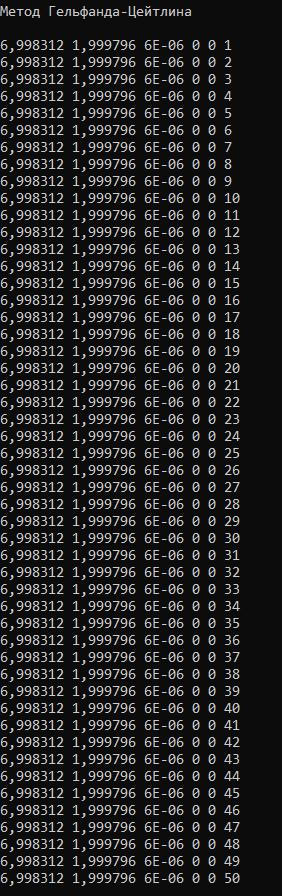
Рисунок 2.6 – Работа программы для функции f1(x) методом Гельфанда-Цейтлина

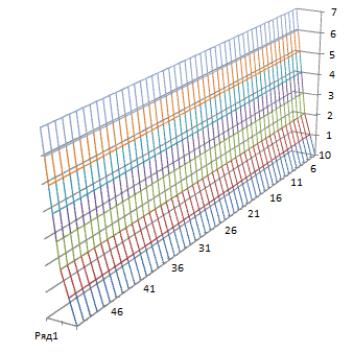
Рисунок 2.7 – График программы для функции f1(x) методом Гельфанда-Цейтлина

2.2.2 Минимизация многомерной функции f2(x)

Функция f2(x) задана формулой f2(x) = (X1 - 2) * (X1 - 2) + (X2 - 7) * (X2 - 7) + 50 * (X2 + 2 * X1 - 6) * (X2 + 2 * X1 - 6) + 7.6

График функции представлен на рисунке 2.8. Исходя из графика можно увидеть, что точка минимума находится по координатам (0,009;6,01).

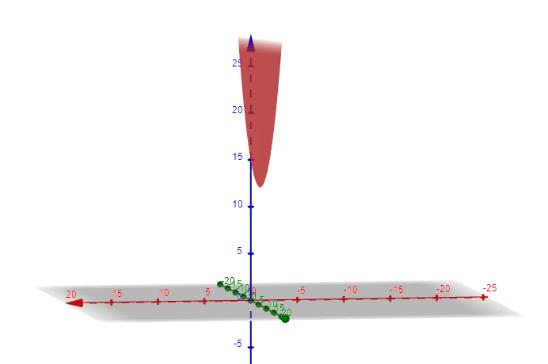
Рисунок 2.8 – График многомерной функции f2(x)

Для каждого метода начальная точка бралась с координатами (0;0). Метод быстрого спуска сошѐлся за 568 итераций, метод Гельфанда-Цейтлина сошѐлся за 30 итераций. Метод Нелдера-Мида работал 17 итераций.

На рисунке 2.9-2.15 представлен результат работы программы для функции

f2(x).

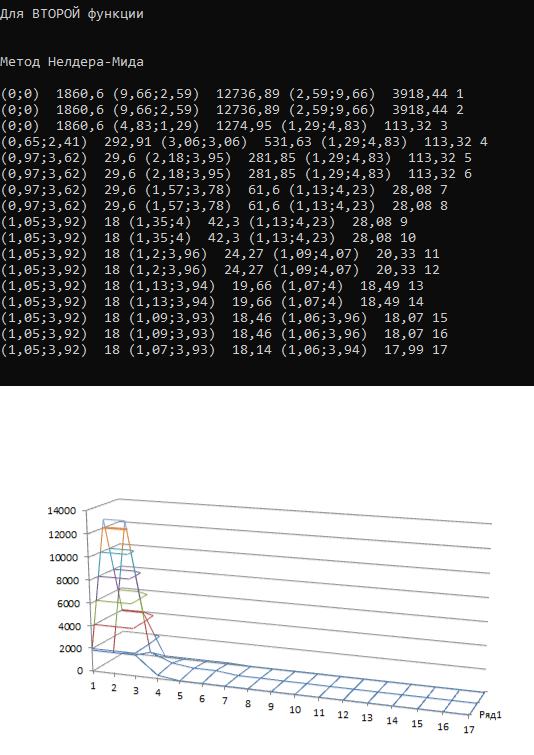
Рисунок 2.9– Работа программы для функции f2(x) методом Нелдера-Мида

Рисунок 2.10 – График программы для функции f2(x) методом Нелдера-Мида

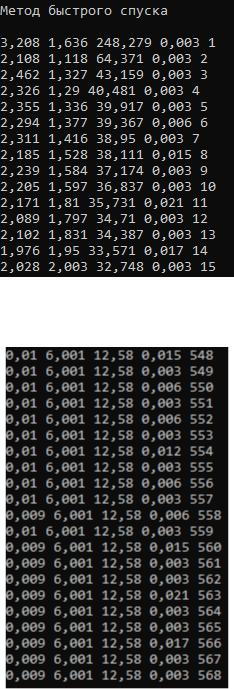
Рисунок 2.11 – Работа программы для функции f2(x) методом Быстрого спуска первые 15 итераций

Рисунок 2.12 – Работа программы для функции f2(x) методом Быстрого спуска последние 20 итераций

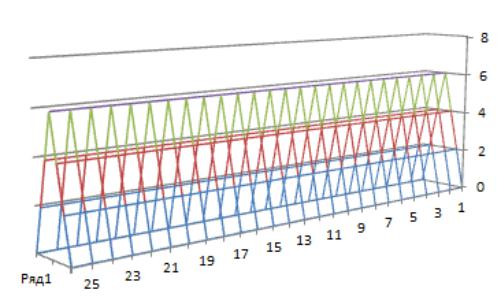
Рисунок 2.13 – График программы для функции f2(x) методом Быстрого спуска последние 20 итераций

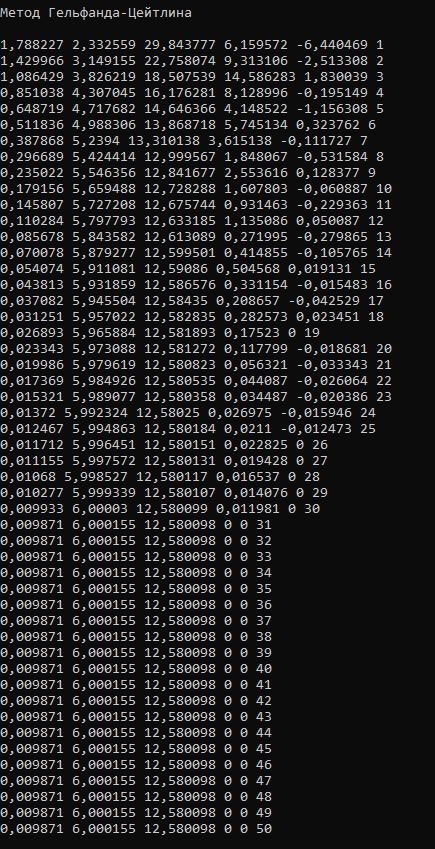
Рисунок 2.14 – Работа программы для функции f2(x) методом Гельфанда-Цейтлина

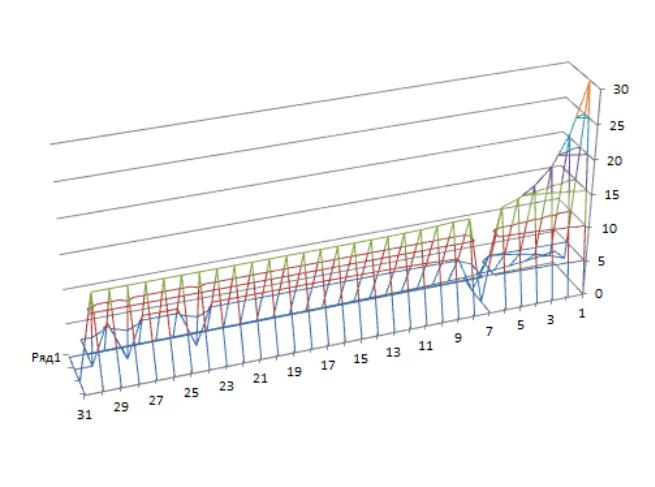
Рисунок 2.15 – График программы для функции f2(x) методом ГельфандаЦейтлина

3Заключение

Входе выполнения лабораторной работы мы ознакомились с методами минимизации одномерных и многомерных функций.

Приложение А

(обязательное)

using System;

namespace Lab1_1

{

internal class Program

{

static void Main(string[] args)

{

int N = 0; double A = 0; double Y = 0;

List<double> xf1 = new List<double>(); List<double> xf2 = new List<double>(); List<double> xf3 = new List<double>(); List<double> yf1 = new List<double>(); List<double> yf2 = new List<double>(); List<double> yf3 = new List<double>();

Console.WriteLine("ЗОЛОТОЕ СЕЦЕНИЕ");

Console.WriteLine("\nПервая функчия");

GoldenRatio(FirstFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1); Console.Write($"Входная тоцка: {A}, Минимальное знацение функчии = {Y} Цисло

итерачий: {N}\n");

A = Y = 0; N = 0; xf1.Clear(); yf1.Clear();

Console.WriteLine("\nВторая функчия");

GoldenRatio(SecondFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1); Console.Write($"Входная тоцка: {A}, Минимальное знацение функчии = {Y} Цисло

итерачий: {N}\n");

A = Y = 0; N = 0; xf1.Clear(); yf1.Clear();

Console.WriteLine("\nТретья функчия");

GoldenRatio(ThirdFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1); Console.Write($"Входная тоцка: {A}, Минимальное знацение функчии = {Y} Цисло

итерачий: {N}\n");

A = Y = 0; N = 0; xf1.Clear(); yf1.Clear();

Console.WriteLine("МЕТОД ДИХОТОМИИ");

Console.WriteLine("\nПервая функчия");

DihMeth(FirstFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2); Console.Write($"Входная тоцка: {A}, Минимальное знацение функчии = {Y} Цисло

итерачий: {N}\n");

A = Y = 0; N = 0; xf2.Clear(); yf2.Clear();

Console.WriteLine("\nВторая функчия");

DihMeth(SecondFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2); Console.Write($"Входная тоцка: {A}, Минимальное знацение функчии = {Y} Цисло

итерачий: {N}\n");

A = Y = 0; N = 0; xf2.Clear(); yf2.Clear();

Console.WriteLine("\nТретья функчия");

DihMeth(ThirdFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2); Console.Write($"Входная тоцка: {A}, Минимальное знацение функчии = {Y} Цисло

итерачий: {N}\n");

A = Y = 0; N = 0; xf2.Clear(); yf2.Clear();

Console.WriteLine("МЕТОД ФИБОНАЦЦИ");

FibonachiMethod(FirstFunction(), 0, 10, ref N, ref A, ref Y, ref xf3, ref

yf3);

Console.Write($"Входная тоцка: {A}, Минимальное знацение функчии = {Y} Цисло итерачий: {N}\n");

A = Y = 0; N = 0;