
PETROV / ____. ____ ____. ______ No.5 [2013-2014]
.pdf
Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Структура счетчика времени Петри-сетевой модели DES
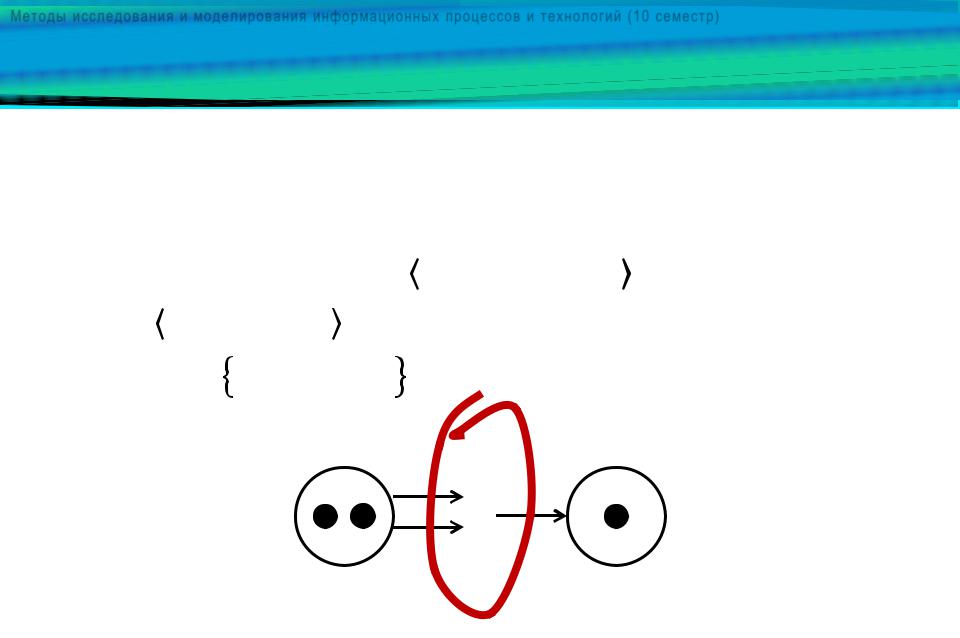
Счетчик времени модели DES, представленной сетью Петри , , , , , является ее входом и представляет
собой наперед заданное множество = : >0 временных последовательностей
|
= |
, |
, … |
|
|
|
1 |
2 |
|
|
|
, |
|
|
+, |
= 1, 2, … |
|
|
>0 |
|
, |
|
|
где >0 |
|
— множество временных переходов с |
|||
ненулевой задержкой;0 — множество переходов с нулевой
задержкой;
= 0 >0
21
Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Временная сеть Петри
Временная сеть Петри представляет собой кортеж
= , , , , ,
где , , , , — маркированная сеть Петри;
= |
|
: |
|
— счетчик времени. |
||
|
|
|
>0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 1 2
22

Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Моделирование параллельных и последовательных вычислений
1, 3  2, 3
2, 3  С, 3
С, 3
1, С |
2, С |
4 |
F |
23

Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Временная Петри-сетевая модель
базовой СМО |
|
|
|
|
|||
|
|
|
|
|
|
|
" " |
|
|
|
|
|
|
|
|
|
|
|
" " |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
, , |
= |
, , |
>0 = |
, |
|
|
|
|||||||||
|
|
|
|
|
|
0 = |
0 |
1 |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
, , … |
|
|
|
= |
, , … |
|
|
|
||||||||
|
|
1 |
|
2 |
|
|
|
1 |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
! |
ВРЕМЕНА НАСТУПЛЕНИЯ -Х СОБЫТИЙ: |
|
|
|
|
|
|
|||||||||
|
|
|
= |
+ |
, |
|
= 0 |
|
|
|
|
|
|
|||
|
|
|
|
−1 |
|
, |
0 |
|
|
|
|
|
|
|
||
|
|
= max |
−1 |
+ |
|
, |
−1 |
+ |
, |
|
= 0 |
|
|
|
|
|
|
|
|
, |
|
, |
0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Временные модели DES: операции
Автомат |
|
Сеть Петри |
|
|
|
min |
Временной |
− |
max |
Временная сеть |
+ |
|
автомат |
Петри |
|||||
|
|
|
|
25

Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Алгебра (, )
Достаточность для анализа временных моделей операции
поиска минимума (максимума)
и сложения (вычитания) в ведет к мысли о практичности какой-либо алгебраической системы с двумя бинарными операциями + и × (или и ), пригодной для линейного описания нелинейных DEDS с выраженной синхронизацией.
ПОЛУКОЛЬЦО —
алгебраическая система с
2 бинарными операциями,
абелева группа по +,
моноид по ×, в которой +
не имеет обратного элемента.
26

Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Полукольцо (1 / 2)
Полукольцо — алгебраическая структура
= , +,×
состоящая из несущего множества и двух замкнутых относительно него операций: «сложения» + и «умножения» ×, — таких что для любых , , выполняется ряд аксиом.
Идемпотентное полукольцо — полукольцо с идемпотентной операцией +.
27

Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Полукольцо (2 / 2)
Идемпотентное полукольцо (аксиомы):
коммутативность сложения:
ассоциативность сложения:
ассоциативность умножения:
существование нуля :
поглощение нулем :
+ = + ;+ + = + + ;
× × = × × ;: + = + = ;× = × = ;
существование единицы : |
: × = × = ; |
|
левая и правая дистрибутивность × по конечным суммам: |
|
|
+ × = × + × |
|
|
× + = × + × |
|
|
идемпотентность сложения: |
+ = . |
28 |
|
|
|

Методы исследования и моделирования информационных процессов и технологий (10 семестр )
Алгебра max, +
Начиная с работы: Cohen, G., et al. ―Algebraic Tools for the Performance Evaluation of Discrete Event Systems‖ (Proc. of the IEEE, Vol. 77, No. 1, pp. 39–58, 1989), современное моделирование систем проявляет интерес к алгебраической системе ±∞, , , где
±∞ = −∞ +∞
, ±∞: = max , |
= + |
|||
Здесь |
= −∞ |
= 0 |
|
|
|
|
|
+ |
+ |
В частности, |
|
= |
+ |
+ |
29

Методы исследования и моделирования информационных процессов и технологий (10 семестр )
max, + -алгебраическая модель базовой СМО (1 / 2)
В традиционной записи времена наступления -х событий в базовой СМО равны
|
|
= |
−1 |
+ , |
|
0 |
= 0 |
|
|
, |
|
|
|
|
|
= max |
|
−1 |
+ |
|
, |
−1 |
+ |
, |
|
0 |
= 0 |
|||||||
|
|
|
|
|
, |
|
|
, |
|
|
|
||||||||||
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= , |
|
|
= , |
|
|
|
> , |
= 1, 2, … |
|||||||||||
, |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
+1 |
= |
|
+ , |
|
= |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
= max |
−1 |
+ |
|
, |
−1 |
+ , |
|
0 |
= 0 |
|||||||||
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||
30
