1.5. Определим графически коэффициент перекрытия:

, что согласуется с аналитическим расчетом.

1.6. Выводы:

Спроектировано и построено эвольвентное зубчатое зацепление. Выбранные коэффициенты смещения обеспечивают отсутствие подреза и заострения: >,>и плавность зацепления. Построенные двумя способами зубья совпадают.

Приложение 1.

z₁= 9, z₂= 18 – число зубьев 1-го и второго колес соответственно,

m=12.00 - модуль,

=0.35(рад) – угол наклона зубьев,

=20˚ - угол главного профиля,

ha*=1.00 – коэффициент высоты зуба,

c*=0.23 – коэффициент радиального зазора.

r₁=57.4658000, r₂=114.931199 – радиусы делительных окружностей;

r_b1=53586394, r_b2=107.172788 – радиусы начальных окружностей;

P_T=40.118557 – шаг по делительной окружности;

m_T=12.770133 – модуль;

ha*_T=0.939693 - коэффициент высоты зуба;

с*_T=0.234923 - коэффициент радиального зазора;

=0.369536 - угол главного профиля,

=14.000000,

=0.335605, =-0.268484 – минимальные коэффициенты смещения.

x₁=0.568000, x₂=0.312000 – коэффициенты смещения;

S₁=25.678211, S₂=23.145734 – толщины зубьев по делительной окружности;

S_a1=5.223136, S_a2=9.556796 - толщины зубьев по окружности вершин;

r_w1=60.693115, r_w2=121.346231 – радиусы основных окружностей;

r_a1=75.163865, r_a2=129.360311 – радиусы окружностей вершин;

=44.526385, =34.056805

r_f1=49.719035, r_f2=103.915481 – радиусы окружностей впадин;

=1.775360, =0.353349 – коэффициенты скольжения;

=1.060041, =0.660756,=1.720797 – коэффициенты перекрытия;

a_W=182.079346 – межосевое расстояние;

h=25.444830 – высота зуба;

=28.004918 – угол главного профиля.

2. Проектирование планетарного зубчатого механизма с цилиндрическими колесами.

Цель: спроектировать планетарный редуктор, обеспечивающий передаточное отношение .

1. Передаточное отношение редуктора .

Из уравнения передаточного отношения определяем значение выраженияи раскладываем его на сомножители

.

Согласно формулам

Получим 6 вариантов значений чисел зубьев.

Наиболее подходящий по соображениям габаритности вариант:

.

2 . Проверяем условие сборки гдеN – целое число.

Примем Р=3. В результате расчета N должно оказаться целым числом

- условие сборки выполняется.

3. Проверяем условие соседства по неравенству >,

>,

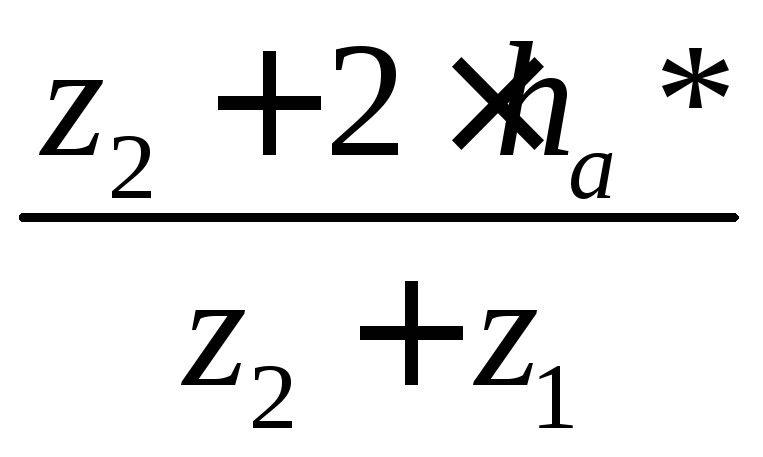0.866>0.465 - ­ условие соседства выполняется.

4. Расчетный угол поворота водила:

˚+3 полных оборота водила.

5. Найдем радиусы колес:

модуль колес m=1,

6.Определим графически передаточное отношение:

,

,

,

.

Отклонение: %=4.3%, что меньше допустимого значения отклонения равного 5%.

Выводы:

Спроектирован планетарный редуктор, обеспечивающий передаточное отношение , что подтверждают аналитический и графический расчет с допустимым отклонением между ними. Так же выполняются условия сборки, соседства и соосности.

3. Динамическое исследование механизма при установившемся режиме движения.

Цель: рассчитать маховик, который обеспечит заданную неравномерность вращения; получить закон движения звена приведения.

3.1. . Определение передаточных функций скоростей кривошипно-ползунного механизма.

Исходные данные для расчета приведены в таблице 1.

Таблица 1.

Наименование параметра	Обозначение	Размерность	Числовое значение
1.Средняя скорость поршня		м/с	7.2
2.Отношение длины шатуна к длине кривошипа		-	4.10
3.Отношение расстояния от точки В до центра тяжести шатуна к длине шатуна		-	0.28
4.Число оборотов коленчатого вала при номинальной нагрузке		об/мин	3800
5.Диаметр цилиндра	d	м	0.073
6.Число оборотов коленчатого вала при холостом ходе		об/мин	550
7.Максимальное давление в цилиндре при холостом ходе		Па
8.Вес шатуна		Н	4.1
9.Вес поршня		H	2.5
10. Момент инерции шатуна			0.0013
11.Момент инерции коленчатого вала			0.008
12.Коэффициент неравномерности вращения коленчатого вала при холостом ходе двигателя		-

Главный механизм проектируется по ходу поршня и принятому коэффициенту отношения к длине кривошипа  = 4.1, как для стационарной машины ,,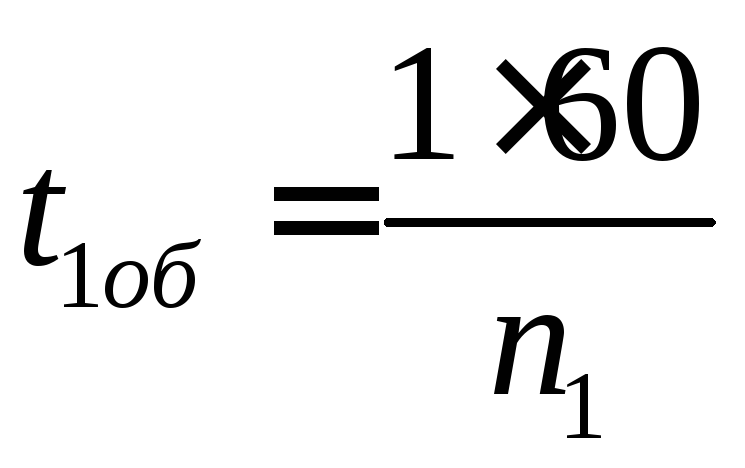, отсюда:(м);

(м).

Вычерчиваем план механизма в 12 положениях.

Масштаб плана : _l = 1000 (мм / м).

Для каждого из положений механизма строят план возможных скоростей, задавшись произвольным постоянным отрезком мм, соответствующим скорости точкиB. Скорость точки C определится по векторной формуле V_С = V_B + V_ВC, а скорость V_S2 = V_B + V_S2B. Данные кинематического исследования сведены в таблицу 2 , где pc, ps₂, bc отрезки, снятые с планов скоростей и соответствующие возможным линейным скоростям V_C,V_S2,V_CB. В этой же таблице приведены значения передаточной функции U₂₁ и аналогов скоростей. По данным таблицы строим графики передаточной функции и аналогов скоростей точек звеньев.

Таблица 2.

Положение механизма	0	1	2	3	4	5	6	7	8	9	10	11	12
(pc)y, мм	0	-30,32	-53,91	-50	-32,69	-19,68	0	19,68	32,69	50	53,91	30,32	0
bc, мм	50	43,63	27,16	0	27,16	43,63	50	43,63	27,16	0	27,16	43,63	50
ps2z, мм	-25,61	-40,78	-45,45	-35,36	-15,79	5,42	25,61	40,78	45,45	35,36	15,79	-5,42	-25,61
ps2, мм	36,07	40,8	49,65	50	44,17	39,05	36,07	40,8	49,65	50	44,17	39,05	36,07
Vqcy, м	0	-0,017	-0,031	-0,028	-0,019	-0,011	0	0,011	0,019	0,028	0,031	0,017	0
U21	-0,25	-0,22	-0,136	0	0,136	0,22	0,25	0,22	0,136	0	-0,136	-0,22	-0,25
Vqs2z, м	-0,015	-0,023	-0,026	-0,02	-0,009	0,003	0,015	0,023	0,026	0,02	0,009	-0,003	-0,015
Vqs2, м	0,02	0,023	0,028	0,029	0,025	0,022	0,02	0,023	0,028	0,029	0,025	0,022	0,02