Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

DSP / cos_lab2

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

654.36 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Отчет по лабораторной работе № 2 «Дискретное преобразование Фурье»

дата	Оценка	Бонус за	подпись
	(max 5)	сложность

Цели работы:

Исследовать свойства преобразования Фурье для дискретных сигналов.

Задачи работы:

1.Изучение процессов и особенностей применения ДПФ к дискретным сигналам.

2.Изучение свойств ДПФ на практике.

3.Научиться применять инструменты программного пакета MatLab для ДПФ.

4.Ознакомиться с модулем SpTool

Краткий конспект теоретической части

Теорема Фурье _______________________________________________________________

_____________________________________________________________________________

Дискретное Преобразование Фурье_______________________________________________

_____________________________________________________________________________

Свойства ДПФ ________________________________________________________________

_____________________________________________________________________________

Быстрое преобразование Фурье _________________________________________________

_____________________________________________________________________________

____________________________________________________________________________

_____________________________________________________________________________

1.Дискретное преобразование Фурье в программном пакете MatLab

Втаблице 1 представлены функции MatLab, используемые для работы с ДПФ.

Таблица 1 – Функции Matlab для работы с ДПФ

	Функция	Описание
		Вычисляет прямое ДПФ для вектора X ;
	y = fft(x)	если X -матрица, то преобразование
	y = fft(x)	производится для каждого столбца в
		производится для каждого столбца в
		отдельности
		Предварительно приводит данные к размеру
	y = fft(x, N)	N , урезая их или дополняя нулями. Размер
	y = fft(x, N)	N обычно задается как 2 в некоторой
		N обычно задается как 2 в некоторой
		степени.
	x = ifft(y)	аналогичные команды для вызова функции
	x = ifft(y, N)	обратного ДПФ.

В результате применения функции fft получим комплексную составляющую спектра исходного сигнала, представленную в алгебраической форме. По составляющим вектора X можно определить модуль, отдельно действительную и отдельно мнимую составляющие спектра.

Задание: разработать скрипт для построения графиков анализируемого сигнала, действительной и мнимой составляющей сигнала и график модуля гармоник согласно Вашему варианту.

N=8;	%Количество отсчетов.
n=0:1:7;	%Индексы	отсчетов.
t=1/8000;	%Частота	дискретизации.

x=sin(2*pi*1000*n*t)+0.5*sin(2*pi*2000*n*t+3*pi/4);%Входной сигнал.

figure(1)
plot(x),grid on	%График анализируемого сигнала.
y=fft(x)	%Преобразование Фурье.
figure(2)	%График действительной составляющей.
stem(real(y)),grid on
figure(3)
stem(imag(y)),grid on	%График мнимой составляющей.
Xm=abs(y)
figure(4)	%График модуля гармоник.
stem(Xm),grid on
Xmm=2*abs(y)/N
figure(5)
stem(Xmm),grid on	%График модуля гармоник (нормированный).

(вклейте разработанную Вами программу)

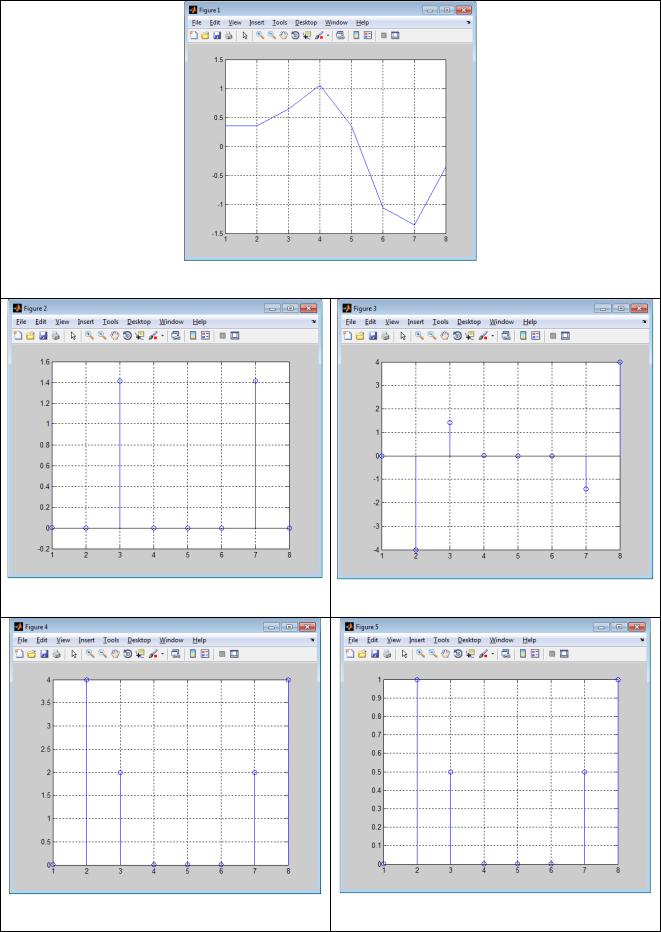
Вклейте полученные графики в соответствующие поля:

Рисунок 1 – Исходная последовательность

Рисунок 2 – Действительная часть ДПФ

Рисунок 3 – Мнимая часть ДПФ

Рисунок 4 – Ненормированный модуль ДПФ

Рисунок 5 – нормированный модуль ДПФ

Выводы: _________________________________________________________________

________________________________________________________________________________

Эффект растекания спектра

При ДПФ мы предполагали (умалчивая), что последовательность отсчетов анализируемого сигнала является периодически продолженной вперед и назад во времени. При этом, если значения начальных и конечных отсчетов сигнала сильно отличаются, при периодическом повторении на стыках сегментов возникают скачки, из-за которых спектр сигнал расширяется.

Задание: разработать скрипт для построения характеристик на частоте, кратной и не кратной гармонике согласно вашему варианту.

N=32;

n=0:1:31;

t=1/32000;

x=sin(2*pi*8000*n*t);

y=fft(x);

xp=fftshift(y) f=-N/2:1:(N/2-1) a=abs(xp)/16 figure(1) stem(f,a),grid on

x2=sin(2*pi*8500*n*t);

y2=fft(x2);

xp2=fftshift(y2)

a2=abs(xp2)/16

figure(2) stem(f,a2),grid on

(вклейте разработанную Вами программу)

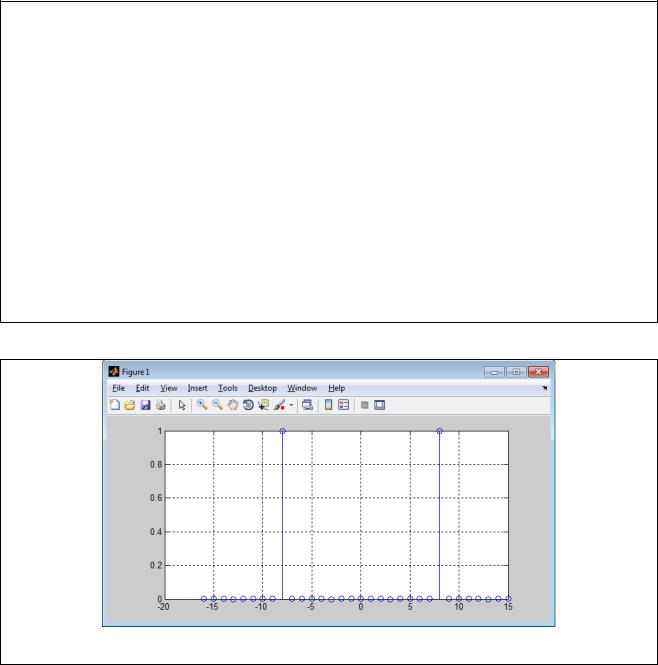
Вклейте результаты выполнения скрипта:

Рисунок 8 – Спектр сигнала для частоты ______Гц

Выводы: _________________________________________________________________

________________________________________________________________________________

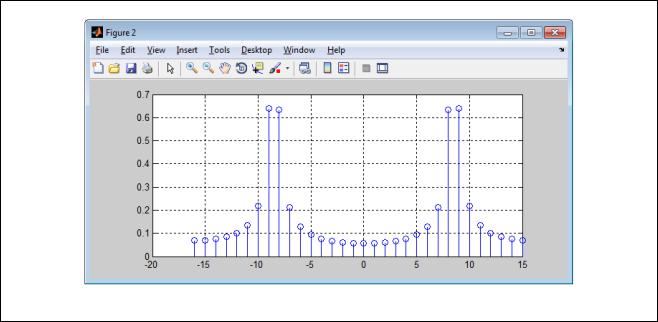
Рисунок 9 – Спектр сигнала для частоты __8500_Гц

Выводы: _________________________________________________________________

________________________________________________________________________________

Спектр меандра

Меандр – это последовательность прямоугольных импульсов со скважностью, равной двум. В спектре меандра присутствуют только нечетные гармоники:

s(t)

cos

cos 3

cos 5

Гармоники, образующие меандр имеют амплитуду, обратно пропорциональную номеру соответствующей гармоники.

Задание: разработать код m-файла, результатом выполнения которого являются графики меандра, реализованные с различным количеством гармоник (1,2,…, 10, 25, 100 и др.)

N=5;

fs=100; t=-1:1/fs:1-1/fs;

nh=(1:N)*2-1; y=cos(2*pi*nh'*t/T);

Am=2/pi./nh; Am(2:2:end)=-Am(2:2:end); s1=y.*repmat(Am',1,length(t)); s2=cumsum(s1);

for k=1:N subplot(2,2,k) plot(t, s2(k,:))

end

(вклейте разработанную Вами программу)

Вклейте результаты выполнения скрипта:

Рисунок 10 – Графики меандра, содержащего различное число гармоник

Функции Matlab, использованные в примере

Функция sum(X) в случае одномерного массива возвращает сумму элементов массива; в случае двумерного массива - это вектор-строка, содержащая суммы элементов каждого столбца.

Функция cumsum(X), кроме того, возвращает все промежуточные результаты суммирования.

Пример:

Рассмотрим массив M:

M = 8 1 6

35 7

49 2

Результаты выполнения функций:

cumsum(M)			sum(M)
8	1	6	15 15 15
11 6		13	15 15 15
11 6		13
15	15	15

Функция repmat(A,M,N) - формирование массива из частей - использует преимущество векторизации. Она имеет три входных аргумента: массив A, количество строк М и столбцов N для вновь создаваемого массива.

Функция repmat возвращает массив B , который использует массив A в качестве основы для построения блочной матрицы с количеством блоков MxN.

Пример:

A = [1 2 3; 4 5 6];

B = repmat(A, 2, 3);

Результаты выполнения функции:

B =
1	2	3	1	2	3	1	2	3
4	5	6	4	5	6	4	5	6
1	2	3	1	2	3	1	2	3
4	5	6	4	5	6	4	5	6

Выводы: _________________________________________________________________

________________________________________________________________________________

Задание: разработать скрипт Matlab, результатом которого являются графики ДПФ меандра при использовании различного количества гармоник.

(вклейте разработанную Вами программу)

Вклейте результаты выполнения скрипта:

Рисунок 11 – Графики спектра меандров с различным числом гармоник

Выводы: _________________________________________________________________

________________________________________________________________________________

1 / 21 2 > Следующая >>>

Соседние файлы в папке DSP

#
10.02.2015548.58 Кб29cos_lab1.pdf
#
10.02.2015654.36 Кб34cos_lab2.pdf
#
10.02.2015750.44 Кб29cos_lab3.pdf
#
10.02.2015763.29 Кб26cos_lab4.pdf
#
10.02.2015665.34 Кб29cos_lab5.pdf
#
10.02.2015444.06 Кб25cos_lab6.pdf
#
10.02.2015319.63 Кб23cos_lab7.pdf