рк элтех
.pdf
WL max LI 2 .
2.6.3. Напряжение на индуктивности в комплексной форме.
Так как напряжение на катушке:
|
|
|
|
u(t) xL Im sin t |
2 |
|
, |
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
2 |
|
||
то U xL Ie |
|
|
|
jxL I |
Здесь jxL j L - индуктивное сопротивление в комплексной форме.
|
|
|
|
|
Оператор e j 2 j отражает |
дифференцирование напряжения на |
|||
индуктивности. |
|
|
|
|
Закон Ома в комплексной форме: |
|
|
|
|
|
|
|
|
|
UL jxL I |
|
I |
U |
|
или |
jxL |
|||
|
|
|
||
Вектора тока и напряжения на комплексной плоскости приведены на рис. 2.5е.
19. Емкость в цепи синусоидального тока.
Емкость отражает явление накапливания электрического поля и характеризуется зависимостью заряда q от напряжения u : C uq
а) |
|
|
б) |
x |
в) xС |
|
Im |
|
|
|
|
|
|
y |
|
|
Um |
д) |
|
W(t) |
|
|
CU2 |
|
CU2 |
t |
2 |
|
г) |
i,u,p |
p(t) |
|
||
|
|
u(t) |
|
i(t) |
|
|
|
t |
|
|
|
|
|
Q |
е) |
jIm |
|
|
||
|
|
Rl |
|
|
|
|
|
UC |
Рис.2.6 |
|
|
2.7.1. Мгновенное значение напряжения на конденсаторе:
u(t) C1 i(t)dt
Пусть i(t) Im sin t , тогда напряжение на конденсаторе:
|
|
|
I |
m |
|
|
|
|
|
|
|
|
|
|
u |
|
(t) |
|
sin t |
|
|
I |
|
x sin t |
|
|
|||
C |
|
|
|
m |
||||||||||
|
|
C |
|
|
2 |
|
|
C |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Um sin t |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Это напряжение отстает от тока на угол 2 .
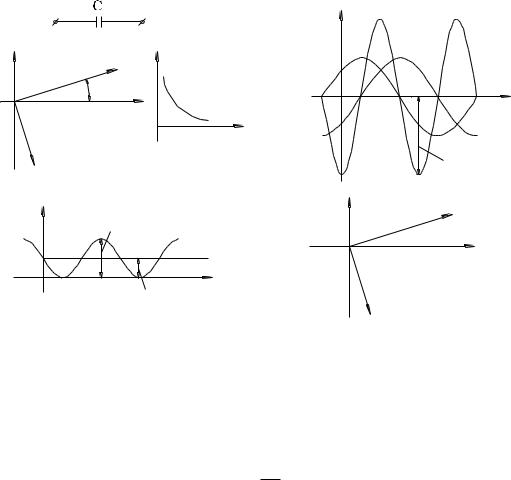
Векторы тока и напряжения приведены на рис.2.6б.
Закон Ома для емкости:
Im |
|
|
|
U |
|
I |
|
1 |
I x |
или |
m |
m |
|
||||||
|
Um C |
|
|
C |
m C , |
||||
|
|
|
|
|
|
|
|
|

|
xC |
|
1 |
|
|
где |
|
- емкостное сопротивление, измеряется в омах (Ом). |
|||
C |
|||||
|
|
Емкостное сопротивление уменьшается с ростом частоты. Зависимость xC от частоты приведена на рис. 2.6.в.
2.7.2. Мгновенная мощность на конденсаторе:
|
|
Im sin t |
p(t) u(t) i(t) Um sin t |
|
|
|
2 |
|
Um Im sin 2 t UI sin 2 t Q sin 2 t
2
Q – реактивная мощность конденсатора. Временные диаграммы uC (t) , i (t), p
(t) приведены на рис. 2.6г.
Среднее значение мощности равно нулю, т.е. рассеивание мощности или потери отсутствуют. Энергия электрического поля в конденсаторе равна:
|
|
|
|
T |
T |
|
|
|
|
|
|
|
|
CuC2 |
(t) |
|
|
W (t) p(t)dt uC |
(t) i(t)dt |
|
|
|
|||||||||||||
2 |
|
|
|||||||||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
CU |
m |
|
2 |
|
|
|
|
CU 2 |
|
|
|
|
||||
|
|
sin |
t |
|
|
|
|
m |
1 cos 2 t |
|
|||||||
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
|
CU |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
C |
1 cos 2 t |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
График WC (t) приведен на рис. 2.6д. |
|
|
|
|
|
||||||||||||
Максимальная энергия электрического поля равна: |
|
|
|||||||||||||||
|
|
|
|
|
|
W |
|
|
|
|
Cu2 |
|
|
|
|||
|
|
|
|
|
|
C max |
|
|
|
C |
|
|
|
||||
2.7.3. Напряжение на емкости в комплексной форме.
|
uC |
|
|
|
Так как |
(t) xC Im sin t |
|
, |
|
|
|
2 |
|
|
|
|
j |
|
|
То |
j |
e |
2 |
|||
U xC Ie |
|
|
|
jxC I . |
Здесь jxC - емкостное сопротивление в комплексной форме.
j
Оператор e 2 отражает интегрирование тока в формуле напряжения на емкости.
|
|
|
|
U |
|
|
|
|
|
I |
|
|
|
|
|
|
. Векторы |
|||
|
jx |
|
||||
Закон Ома в комплексной форме UC |
jxC I или |
|
|
|||
|
|
|
|
|
C |
|
U C |
и I приведены на рис. 2.6е. |
|
|
|
|
|
20. Комплексный метод расчета. Преобразования элементов при переходе из временной в комплексную форму.