РПЗ

3. Проектирование зубчатых механизмов

3.1 Исходные данные для проектирования

3.2 Геометрический расчет эвольвентной зубчатой передачи.

Геометрические параметры

Коэффициенты суммы смещений:

Толщины зубьев шестерни и колеса по дугам делительных окружностей:

- 21 -

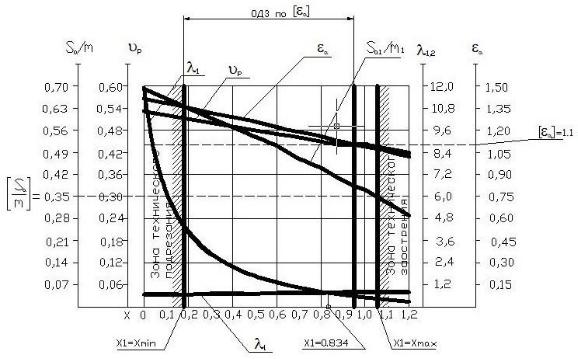
На основе полученных данных на графическом листе 3 были построены графики изменения величин качественных показателей в зависимости от коэффициента смещения x1 (рис.3).

Выбираем термообработку зубчатой передачи – азотирование. Тогда допустимое

Степень точности колес берется 8-я. Тогда допустимый коэффициент перекрытия берется равным [ ] = 1,10.

С учетом равномерного износа колес, условия подреза и отсутствия заострения зубьев, коэффициент смещения выбирается равным x1 0,834 .

рис. 3

3.4 Результаты расчета зубчатой передачи

3.5 Построение станочного и зубчатого зацеплений

Масштаб на чертеже с учетом рекомендаций выбран l 8 мм мм .

На графическом листе 3 приведено построение станочного зацепления и передачи, а также графики качественных показателей зубчатой передачи в функции смещения исходного производящего контура..

Профиль зуба шестерни образуется как огибающая ряда положений исходного производящего контура реечного инструмента в станочном зацеплении. Такое образование профиля отражает реальный процесс изготовления колеса на станке. При этом эвольвентная часть профиля зуба образуется прямолинейной частью реечного производящего исходного контура, а переходная кривая профиля зуба – закругленным участком.

Для построения станочного зацепления используется метод обращенного движения. Шестерня рассматривается как неподвижное звено. Рейка, совершая сложное движение, обкатывает шестерню.

Для построения профиля зуба колеса используем способ образования эвольвенты при перекатывании производящей прямой по основной окружности.

Для указанных построений поставлены основные размеры.

На чертежах зубчатого и станочного зацеплений показаны активные участки зубьев, нагруженные контактными напряжениями.

3.6 Проектирование планетарного редуктора

3.6.1 Исходные данные

Двухрядный планетарный редуктор с двумя внешними зацеплениями. Число сателлитов К=3. Передаточное отношение редуктора

U H 10 7 20 .5

7 – угловая скорость входного звена редуктора;5 - угловая скорость выходного звена редуктора (угловая скорость колеса 5).

- 24 -

3.6.2 Расчет числа зубьев колес.

Расчет производиться по стандартной методике изложенной в [5]. При проектировании нужно использовать ниже перечисленные условия.

Уравнение передаточного отношения:

Уравнение соосности:

z10 z11 z12 z13

(z10 z11) (z12 z13)

Условие отсутствия подрезания

zi zmin 17

Условие сборки:

z10U10 H 1 kP Ц , k

где k – число сателлитов; P = 0,1,2,3… - целое число; Ц – любое целое число. Условие соседства:

Также при проектировании следует учитывать условие наименьших габаритов и сумму чисел зубьев – косвенно определяющую массу и трудоемкость изготовления. Составив систему уравнений из условия соосности получим:

Условие выполняется. Соседство сателлитов обеспечено. Проверка условия сборки:

Условие сборки выполняется. Сборка возможна.

На графическом листе 3 показана схема и проведен графический расчет передаточного отношения планетарного редуктора.

- 25 -

- 26 -

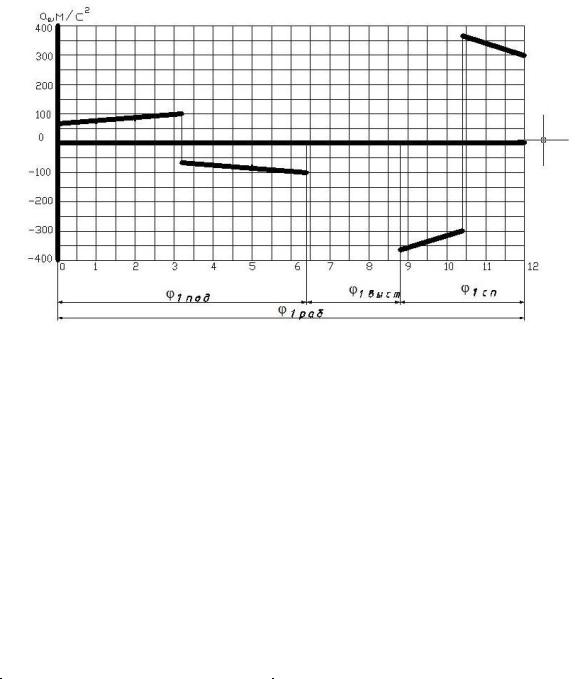
4. Проектирование кулачкового механизма.

4.1 Исходные данные для проектирования.

Дано: закон изменения ускорения точки В толкателя:

рис. 4

4.2 Построение кинематических диаграмм методом графического интегрирования.

Так как исходная функция задана в виде графика, то решение получают при помощи графического метода. Для определения передаточной функции скорости толкателя интегрируют заданную функцию ускорения толкателя, затем интегрируют полученную функцию скорости и находят функцию перемещения

График скорости толкателя получают методом графического интегрирования из графика ускорения толкателя. Для этого на продолжении оси графика ускорений

с левой стороны выбирают отрезок интегрирования OK1 40 мм .

После построения графика скорости строят график перемещений толкателя. Тогда на продолжении оси абсцисс графика скорости также откладывают отрезок

интегрирования OK2 40 мм .

Связь между кинематическими параметрами толкателя, тангенциальным ускорением, скоростью движения и перемещением определяется соотношениями:

VB aBτ dt и SB VB dt

Частота вращения кулачка:

Масштаб времени:

- 28 -

масштаб скорости:

масштаб ускорения:

масштаб передаточной функции скорости:

масштаб передаточной функции ускорения:

4.3 Определение основных размеров кулачкового механизма.

Основные размеры механизма определяют с помощью фазового портрета,

представляющего собой зависимость SB VqB . Для механизма с вращающимся толкателем фазовый портрет строят в полярной системе координат. По оси SB

откладывают перемещение толкателя от начала координат в точке B0 по дуге радиуса lBC , проходящей через эту точку.

Отрезки, соответствующие перемещениям толкателя, откладывают в масштабе графика перемещений. От полученных точек откладывают отрезки кинематических передаточных функций перпендикулярно линии перемещения

Значения SB , VqB и x vq сведены в таблицу 3.1.

- 29 -

Табл.3.1

Ограничивая фазовый портрет лучами, проведенными под заданным [ ], к каждому перпендикуляру к вектору кинематических передаточных отношений. Находим ОДР, внутри которой выбираем положение оси вращения кулачка О и

определяют искомые размеры кулачкового механизма. ( r0 и а ) Расстояние B0O будет являться радиусом r0 :

r0 (B0O) 110.6199 0.069 мS* 1597.235

4.4 Построение профиля кулачка.

При графическом построении профиля кулачка применяется метод обращения движения: всем звеньям механизма условно сообщают угловую

скорость, равную 1 . При этом кулачок становится неподвижным, а остальные

звенья вращаются с угловой скоростью, равной по величине, но противоположной по направлению угловой скорости кулачка.

- 30 -