Локальная теорема Муавра-Лапласа.
Если число испытаний велико (n>100), а вероятности не близки к нулю (npq>20), то вероятность m появлений события равна 1/(npq) умноженное на функцию лапласа от значения m минус мат ожидание (np), деленное на среднеквадратическое отклонение – корень из npq. Значения функции лапласа в конце учебника.
Чем больше число наблюдений, тем точнее будет вычислена вероятность.
Закон распределения вероятностей
Закон распределения вероятностей - это закон, описывающий область значений случайной величины и соответствующие вероятности появления этих значений.
Это теоретическое распределение, которое выражено математически и имеет среднее и дисперсию — аналоги среднего и дисперсии в эмпирическом распределении.
Распределение вероятности показывает вероятности всех возможных значений случайной переменной. Это теоретическое распределение, которое выражено математически и имеет среднее и дисперсию — аналоги среднего и дисперсии в эмпирическом распределении.
Каждое распределение вероятности определяется некоторыми параметрами, параметры служат обобщающими величинами (например среднее, дисперсия), характеризующими данное распределение (т.e. их знание позволит подробно описать распределение).
Функция от случайной величины
Если дана функциональная зависимость одной непрерывной случайной величины от другой, то функции плотностей этих с.в. также зависимы друг от друга. Если одна с.в. дискретна, то дискретна и другая, а закон распределения одной связан с законом распределения другой.
В
случае с непрерывными величинами
плотность одной из них равна плотности
другой, в которой вместо переменной
используется функция зависимости двух
с.в., умноженной на модуль производной
этой функции зависимости.
это
пси, функция зависимости одной с.в. от
другой
Если функция у=пси (от икс) немонотонная, то разбиваем на монотонные отрезки и считаем на каждом из них, затем складывая.
Эффективность точечной оценки
Имеются три урны. В первой 2 белых и 3 черных шаров; во второй 4 белых и 2 черных шаров; в третьей одни белые. Некто подходит наугад к одной из урн и вынимает из нее один шар. Шар оказался белым. Найти вероятность того, что этот шар был вынут из третьей урны.
P(B1) = P(B2) = P(B2) = 1/3
P(A|B1) = 2/5
P(A|B2) = 4/6 = 2/3
P(A|B3) = 1
Непрерывная случайная величина
задана своей функцией распределения
вероятностей:
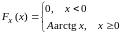
Найти
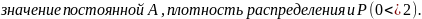
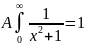
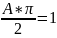
Плотность
распределения:
Совместное распределение системы случайных величин X и Y имеет вид:
-
X\Y
1
2
3
1
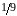
с
2
0
3
0
0
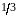
Найти значение постоянной с, законы
распределения случайных величин X и
Y , совместную функцию распределения,
ковариацию,
,
,
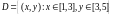проверить независимость X и Y.
Поскольку полная сумма вероятностей в таблице равна единице, постоянная с равна: с = 1 - 1/9 - 1/9 - 1/6 - 1/6 - 1/3 = 2/9
Таким образом, совместное распределение системы (X,Y):
-
X\Y
1
2
3
1
1/9
1/9
2/9
2
0
1/6
1/6
3
0
0
1/3
Закон распределения случайной величины X:
X |
1 |
2 |
3 |
P |
4/9 |
2/6 |
1/3 |
Закон распределения случайной величины Y:
Y |
1 |
2 |
3 |
p |
1/9 |
5/18 |
13/18 |
Совместная функция распределения:
-
X\Y
y≤1
1<y≤2
2<y≤3
y>3
x≤1
0
0
0
0
1<x≤2
0
1/9
2/9
4/9
2<x≤3
0
1/9
7/18
7/9
x>3
0
1/9
7/18
1
Чтобы определить вероятность попадания в интервал, необходимо посмотреть, какие значения попадают в интервал и сложить соответствующие вероятности
P(1≤X≤3, 3≤Y≤5) = FXY(X=1, Y=3) + FXY(X=2, Y=3) + FXY(X=3, Y=3) = 2/9 + 1/6 + 1/3 = 13/18
C. в. Будут независимы, если выполняется условие:
P(X = xi, Y = yi) = P(X = xi) P(Y = yi)
P(X = 1, Y = 1) = 1/9
P(X = 1) P(Y = 1) = 1/9 * 4/9 = 4/81
4/81 ≠ 1/9, следовательно, величины зависимы
8. Дана выборка: 4 1 4 8 4 7 2 5 9 6.
Построить вариационный ряд, статистический ряд и эмпирическую функцию распределения, найти размах выборки, интервал варьирования, выборочную моду, выборочную медиану, выборочные верхнюю и нижнюю квартили, выборочное среднее, выборочную дисперсию и несмещенную дисперсию. Построить полигон частот.
Вариационный ряд: 1 2 4 4 4 5 6 7 8 9
Статистический ряд:
x |
1 |
2 |
4 |
5 |
6 |
7 |
8 |
9 |
n |
1 |
1 |
3 |
1 |
1 |
1 |
1 |
1 |
p |
0,1 |
0,1 |
0,3 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
Эмперическая функция распределения:
Размах выборки: 9-1 = 8
Интервал варьирования:
Выборочная мода: 4
Выборочная медиана: 4,5
Выборочный нижний квартиль: 4
Выборочный верхний квартиль: 7
Выборочное среднее: 5
Выборочная дисперсия:
5,8
Несмещенная дисперсия:
=
2,538
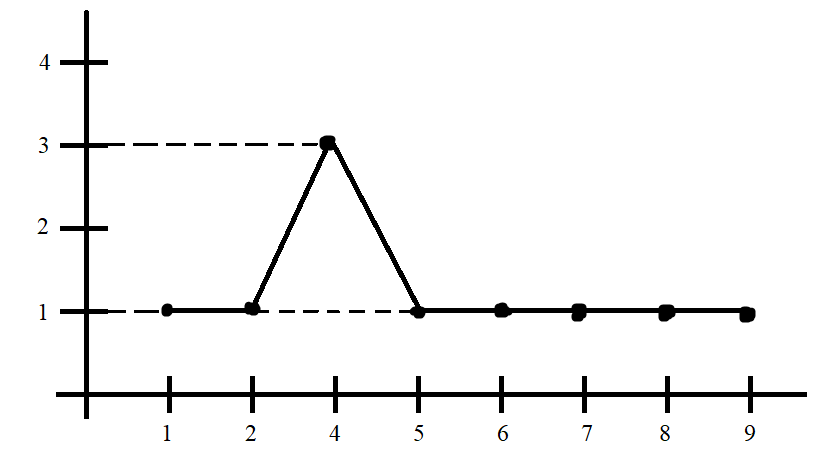
Полигон частот:
