
- •События. Действия над событиями.
- •Классическая вероятность. Свойства вероятностей.
- •Основные правила комбинаторики. Сочетания, размещения, выбор без возвращения и с возвращением.
- •4. Дискретная вероятность и ее свойства.
- •Общее определение вероятности (аксиоматика Колмогорова). Свойства вероятностей.
- •1 Фукнция распределения Лапласа
- •Мат ожидание. Примеры вычисления ( -это)
- •Выборочное среднее
- •Выборочная дисперсия
- •Точечное оценивание. Несмещённость, состоятельность, эффективность
- •Матстат
Оглавление
1. События. Действия над событиями. 2
2. Классическая вероятность. Свойства вероятностей. 3
4. Дискретная вероятность и ее свойства. 5
6. Условная вероятность и ее свойства. 9
7. Независимость событий. Свойства независимых событий. 11
8. Независимость n событий 11
9. Схема Бернулли. Формула Бернулли. Наиболее вероятное число успехов. 13
10. Теорема Бернулли. 14
11. Локальная и интегральная предельные теоремы Муавра - Лапласа. 14
1 фукнция распределения Лапласа 14
12. Теорема Пуассона 16
13. Случайные величины. Функции распределения случайных величин. Характеризационные свойства функций распределения(E - читается кси) 17
14. Случайные величины дискретного типа, примеры 19
15. Случайные величины абсолютно непрерывного типа, плотность распределения, примеры 21
17. Свойства мат ожидания. 28
18. Дисперсия, примеры вычисления 29
19. Ковариация. Коэффициэнт кореляции и его свойства 37
20. Случайные векторы. Функция совместного распределения. Дискретный тип. Абсолютно-непрерывный тип 39
21. Независимость случайных величин. Мат ожидание случайных величин 42
22. Моменты старших порядков. Неравенство Йенсена. Неравенство Ляпунова 43
23. Виды сходимости случайных величин 44
24. Закон больших чисел. Неравенство Маркова. Теорема Чебышева 46
25. Теорема Хинчина. Теорема Колмогорова 48
26. Центральная предельная теорема. Теорема Леви. Теорема Ляпунова 49
27. Цепи Маркова. Конечномерные распределения. Уравнение Чепмена Колмогорова 52
28. Классификация состояний цепи 54
29. Стационарное распределение. Теорема Маркова 56
30. Понятие выборки и генеральной совокупности 58
31. Выборочная функция распределения. Теорема Гливенко. Теорема Колмогорова 59
32. Выборочное среднее 62
33. Выборочная дисперсия 62
34. Точечное оценивание. Несмещённость, состоятельность, эффективность 64
35. Неравенство Рао-Крамера. Количество информации по Фишеру. Эффективные оценки 67
36. Квантили. Вариационный ряд 71
37. Метод моментов. Выборочный метод 74
38. Метод максимального правдоподобия. 75
39. Оценки параметров линейной регрессии 77
40. Доверительный интервал. Доверительный интервал для среднего нормальной совокупности при известной и неизвестной дисперсии 80
41. Проверка статистических гипотез. Ошибки первого и второго рода 84
42. Лемма Неймана - Пирсона. Критерий Неймана - Пирсона. Проверка гипотезы о среднем значении генеральной совокупности с известной дисперсией. 87
43. Критерий хи квадрат (критерий пирсона) 90
44. Критерий Колмогорова 91
45. Проверка гипотезы о среднем значении нормальной генеральной совокупности с известной дисперсией 94
46. Проверка гипотезы о среднем значении нормальной генеральной совокупности с неизвестной дисперсией 95
47. Вопросы на дурачка 96
МАТСТАТ 103
События. Действия над событиями.
1.0 Существует некий эксперемент, который может быть неоднократно повторён в одних и тех же условиях, а исходы эксперемента заранее непредсказуемы.
Неразложимые исходы эксперемента - точки множества омега Ω(универсального множества), w ⊂ Ω - элементарный исход эксперемента.
События(то что происходит в результате эксперемента) будем описывать подмножествами универсального множества, A⊂Ω. Событие - подмножество множества элементарных исходов.
1.1 w благоприпятсвует событию А, если w ∈ A
1.2 Если в результате эксперемента наступел элементарный исход w, благоприпятсвующий событию A, то мы говорим что наступило событие A. Если говорим что наступило событие А, то это означает что наступил один из элементарных исходов, благоприпятсвующий событию А.
1.3 ∅ - это невозможное событие, которое никогда не происходит. Ω - достоверное событие, которое всегда происходит
1.4 Событие ̄̅Ā назовём противположным событием, если оно состоит в том, что А не происходит(Ω\A)
1.5 Произведением событий А и B называется событие C, состоящее в том, что A и B происходят одновременно. С = АB
1.6 Суммой событий А и B насывается событие С, состоящее в том, что происходит хотя бы одно из них. С = A∪B
1.7 Разностью событий А и B называется событие C, состоящее в том, что А происходит, а B не происходит. C = A/B=A̅B
1.8 Если AB = ∅ то эти события несовместные (не происходят одновременно)
1.9 Говорят что А влечёт за собой событие B, если при наступлении события A происходит событие B. A⊂B
Ps пропущены все доказательства кроме самых коротких
Классическая вероятность. Свойства вероятностей.
Число исходов конечно и каждому исходу приписывается одна и та же вероятность, Ω = {w1,..,wn}



Свойства:
Равновозможные
Несовместные
Одно из wn всегда реализуется
Основные правила комбинаторики. Сочетания, размещения, выбор без возвращения и с возвращением.


С повторениями(n различных видов предметов которые нужно разместить по k местам, причём можно выбирать несколько предметов 1 вида):
![]()


![]()
С повторениями(размещение n1 элементов 1 типа, n2 эл. 2 типа.... по n различным местам):



C повторениями(предметы n различных видов, которые нужно объединить в наборы, содержащие k элементов):
![]()
4. Дискретная вероятность и ее свойства.
Рассматриваемое множество Ω состоит из дискретного(конечного, счётного) числа точек Ω={w1,w2,..}
На
множестве эл. исходов Ω
заданы вероятности элементарных исходов,
если на множестве Ω
определена неотрицательная числовая
функция P(w),
такая
что
![]() .
.
Вероятностью
события A
назывется
число
![]()
Свойства вероятностей

![]()
![]()
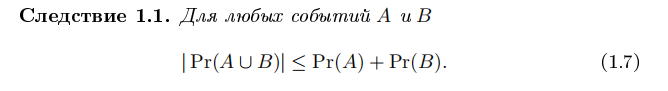


Общее определение вероятности (аксиоматика Колмогорова). Свойства вероятностей.

Сигма алгебра B

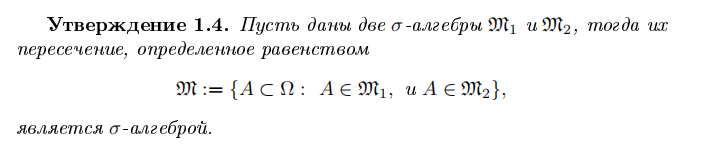


Можно пропустить определение 1,18 и утвер, 1,6

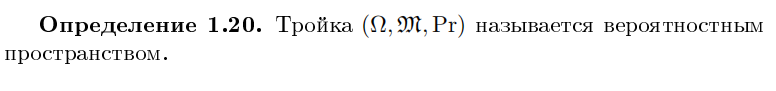
М=F(функция)
Ниже примеры, фиг знает нужны или нет



Условная вероятность и ее свойства.

Формула Баеса, док-во





Тоже не обязательно
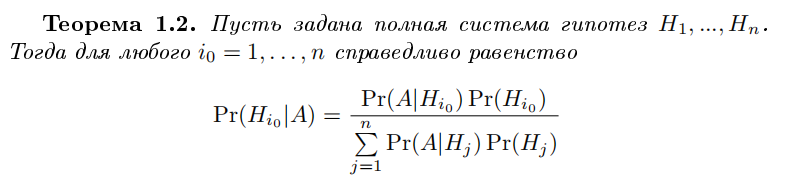
Независимость событий. Свойства независимых событий.



Независимость n событий



НО независимость в совокупности != попарная независимость


Схема Бернулли. Формула Бернулли. Наиболее вероятное число успехов.



ИЛИ

Теорема Бернулли.

(вероятность того, что частота события отличается от вероятности события на величину большую чем эпсилон будет меньше либо равно чем 1 делить на 4n эпсилон квадрат)
Локальная и интегральная предельные теоремы Муавра - Лапласа.
