3. Объем и содержание семинарских занятий

3.1. Семинарское занятие по теме "Гидростатика"

Давление в покоящейся жидкости. Силы давления покоящейся жидкости на плоские и криволинейные стенки. Равновесие жидкости в движущихся сосудах. Решение некоторых задач. Выдача 1-го задания.

Введение. Некоторые теоретические положения.

Давление в покоящейся жидкости - напряжение от действия внешних сил, приложенных нормально и равномерно распределенных по выделенной площадке. За единицу давления в системе единиц СИ принят паскаль - давление, вызываемое силой 1 Н, равномерно распределенной и нормально направленной к поверхности площадью 1 м²: 1 Па = 1 Н/м² = 10^-6 МПа. В технике применяют систему единиц МКГСС (метр, килограмм-сила, секунда), в которой за единицу давления принимается килограмм-сила на квадратный сантиметр: 1 кГс/см² = 0,98^.10⁵ Па. Кроме того, используют внесистемную единицу - бар: 1 бар = 10⁵ Па ≈ 1 кГс/см².

Абсолютное давление - представляющее полное напряжение сжатия от действия всех внешних сил, приложенных к выделенному объему жидкости. За начало отсчета принято такое состояние, возможное в идеализированном пространстве, в котором отсутствуют молекулы любого вещества, т.е. нет сжимающих напряжений.

Атмосферное давление р_атм - абсолютное давление, создаваемое окружающей средой (столбом воздуха, который условно «опирается» на единичную площадку); в общем случае - внешнее абсолютное давление, действующее в конкретной точке пространства, которое не имеет фиксированного значения.

Избыточное давление р_изб - давление, превышающее уровень атмосферного давления, т.е. р_изб = р_абс - р_атм .

Недостаток давления до атмосферного свидетельствует о разреженном состоянии рассматриваемой сплошной среды в сосуде. Такое состояние в технике называют вакуумом. Величину отрицательного избыточного давления (по отношению к атмосферному) р_абс < р_атм , измеряющую величину разрежения, определяют как давление вакуума р_вак = р_атм - р_абс.

Уравнение р = р_сп + r^.g(z₀ - z) = р_сп+ r gh, называемое основным уравнением гидростатики, математически описывает гидростатический закон распределения давления:

- всякое изменение внешнего давления р_сп (на свободной поверхности) вызывает изменение давления во всех точках покоящейся жидкости на ту же величину (закон Паскаля);

- давление внутри объема жидкости линейно зависит от глубины (гидростатический закон распределения давления);

- в одном и том же объеме покоящейся однородной жидкости все частицы, расположенные в одной и той же горизонтальной плоскости, имеют одинаковое гидростатическое давление, т.е. горизонтальные плоскости являются поверхностями равного давления;

- каждому значению давления р можно поставить в соответствие линейную величину р/rg, представляющую собой высоту столба жидкости, создающего в своем основании такое давление;

- для определения давления в произвольной точке объема покоящейся жидкости необходимо знать давление в какой-либо точке этого объема и глубину погружения этой точки или одной точки относительно другой;

- полученный закон справедлив для любого положения плоскости координат х0у, называемой плоскостью сравнения.

Графическое изображение изменения давления в зависимости от глубины вдоль какой-либо стенки, графическое построение которого основано на свойствах гидростатического давления, называют эпюрой давления.

Уровень гидростатического напора Н (плоскость гидростатического напора), определяется от положения горизонтальной плоскости, которая соответствует нулю давления. Поверхность с давлением, соответствующим атмосферному, - пьезометрической поверхностью (ПП).

Поверхность, разделяющую газовую и жидкую среды, называют свободной (СП).

Если плоская наклонная стенка (в общем случае) подвержена одностореннему давлению жидкости, то полная сила давления жидкости Р на площадку равна произведению площади этой площадки на величину гидростатического (избыточного) давления в центре тяжести выделенной площадки P=р_C^.S= r gh_C^.S, где h_C^. - вертикальная координата центра тяжести площадки от пьезометрической поверхности.

Сила давления жидкости на площадку по любому направлению определяют по выражению P = r(gcosa)W_ТД , где W_ТД =(h_C/cosa)S - объем "тела давления", построенного на заданной площадке от пьезометрической поверхности до заданной площадки в направлении действия силы; g^.cosα - ускорение сил тяжести в заданном направлении (например, перпендикулярно заданной площадки); ρW_ТД - масса тела давления, заполненного этой жидкостью. В итоге сила давления Р жидкости на площадку численно равна силе тяжести жидкости в объеме тела давления в заданном направлении (в направлении действия силы Р).

Линия действия этой силы давления жидкости Р пересекает площадку в некоторой точке D, часто называемой центром давления и расположенной ниже центра тяжести С на величину ∆у=J_x0/(y_cS). Чем больше угол a наклона стенки, тем больше ∆у, которое достигает максимального значения при a = 90^о (вертикальная стенка).

Определение полной силы давления жидкости на криволинейную стенку с неравномерным распределением давления сводится к определению главного вектора сил давления по величине и направлению путем вычисления его проекций на оси координат x,y и z. Модуль главного вектора сил определится по формуле: |Р| , а его направление определяется через косинусы направляющих углов (углов, образуемых направления вектора давления с осями координат).

Горизонтальная составляющая силы давления жидкости на криволинейную площадку определяется по правилам нахождения силы давления на плоскую стенку: Р_гор= р_С S_ВЕР, где S_ВЕР - вертикальная проекция криволинейной площадки.

Вертикальная составляющая силы действия жидкости на криволинейную площадку определяется как Р_вер= p_изб S_ГОР+G=rgW_ТД,где S_ГОР - площадь горизонтальной проекции криволинейной площадки, G - сила тяжести жидкости в объеме, ограниченном криволинейной площадкой и свободной поверхностью; W_ТД - объем тела давления, ограниченном криволинейной площадкой и пьезометрической поверхностью. Таким образом, сила Р_вер численно равна силе тяжести тела давления, построенного на данной площадке АВ.

Линия действия горизонтальной составляющей - через центр давления вертикальной проекции криволинейной площадки, вертикальной составляющей сил действия жидкости на криволинейную площадку проходит через центр тяжести тела давления ТД.

Окончательно получаем: .

Суммарная сила давления жидкости на тело определяется как Р_А =r gW_ТЕЛО, где r - плотность жидкости, W_ТЕЛО - объем тела, численно равна силе тяжести жидкости в объеме тела, направлена вверх противоположно силе тяжести тела, не зависит от глубины погружения тела, направленная вверх. Линия действия такой силы должна проходить вертикально через центр тяжести вытесненного объема жидкости. Суммарную силу воздействия жидкости на погруженное в жидкость тело называют выталкивающей силой или силой Архимеда. В этом заключается закон Архимеда: Тело, погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная этим телом жидкость.

Под относительным покоем будем понимать такое состояние, при котором в жидкости отсутствуют перемещения отдельных ее частиц по отношению друг к другу и стенок сосуда. При этом жидкость перемещается как твердое тело. Движение жидкости в этом случае можно называть переносным движением. Характерным для этого состояния будет постоянство формы объема жидкости. В случае если система координат жестко связана со стенками сосуда, приходим к статической задаче, основой для решения которой служит уравнение Эйлера:

dp = r (q_x^.dx+q_y^.dy+ q_z^.dz),

выражающее приращение давления dp при изменении координат и в общем случае равновесия жидкости.

Единичная массовая сила q= g+j. Поле массовых сил q неоднородно.

В случае равновесия жидкости в сосуде, движущемся прямолинейно с постоянным ускорением j = - a. С учетом граничных условий x = 0; z = z₀ и р = р₀ имеем закон распределения давления по объему жидкости:

р = р₀ + r (j - g^.sin a) ^. x - r g(z₀ - z)cosa.

Анализ полученного уравнения позволяет сделать заключения:

1) давление в жидкости меняется по всем направлениям, кроме плоскостей равного давления, которые нормальны суммарному вектору равнодействующей единичной массовой силы q = g + j, где j = - a;

2) давление в жидкости изменяется линейно по любому направлению, кроме оси 0у, которой параллельны плоскости равного давления.

При рассмотрении равновесия жидкости в цилиндрическом сосуде, равномерно вращающемся вокруг вертикальной оси, траектория любой частицы жидкости суть окружность с центром на оси вращения. Для любой частицы жидкости к ускорению силы тяжести g добавляется ускорение переносного движения j = w²r, равное по модулю и противоположное по направлению центростремительному ускорению а, где w - угловая скорость вращения, r -радиус расположения вращаемой частицы.

Подставив эти данные в дифференциальное уравнение равновесия - уравнение Эйлера для находящейся в покое жидкости и ведя граничные условия r₀ , z₀ и p₀ , имеем полное уравнение распределения давления в жидкости, вращающей вокруг вертикальной оси:

p = p₀ + r^.(r² - r₀²)^.w²/2 - r^.g^.(z - z₀),

с помощью которого можно определять давление в любой точке вращающегося объема.

Проведем некоторые исследования:

1). Уравнение параболоида свободной поверхности с избыточным давлением p=0 и расположением вершины с координатами z=z₀ и r=0 (х=0 и у=0) имеет вид z=z₀+w²r²/2g . Отсюда можно заключить - форма поверхности равного давления не зависит от плотности жидкости.

2). При r₀ = r=0 имеем p = p₀ - r g (z - z₀) = p₀ - r gh, т.е. изменение давления во вращающемся сосуде с жидкостью происходит в глубину по вертикали.

3). Для точки М с координатами z_M , r_M и приняв r₀ = 0, получим, что h_М = z_сп -z_М , т.е. глубину погружения точки необходимо исчислять от свободной поверхности, устанавливающейся при вращении сосуда, на радиусе расположения точки М.

4). При определении положения свободной поверхности в решении практических задач следует руководствоваться такими соображениями:

- объем несжимаемой жидкости не изменится при переходе в состояние относительного покоя, но конечно изменится форма объема жидкости (жидкость не вытекает); поверхности равного давления естественно примут форму параболоидов вращения.

Равенство первоначального и полученного при вращении объемов, выраженное аналитически, позволяет окончательно определить положение, например, свободной поверхности, для которой р = р₀.

Для проведения аналитических выкладок следует помнить, как выражаются:

высота параболоида ;

объем параболоида .

П ри вращении герметично закрытого сверху крышкой и полностью заполненного жидкостью под избыточным давлением р_изб = р_М цилиндрического сосуда с размерами D х Н (рис.1.1) вокруг вертикальной оси с угловой скоростью вращения w, создается вертикальная сила, действующая на крышку AD. Величина силы определяется по выражению:

,

Здесь р_изб = р_М - избыточное давление жидкости внутри сосуда до вращения; р_вр - давление на крышке AD от вращения сосуда; W_ABCD - объем тела давления при учете действия избыточного давления; W_BEFC - объем тела давления, возникшего при вращении сосуда с жидкостью. Таким образом, сила, действующая на крышку вращающегося сосуда, численно равна весу "тела давления", построенного между крышкой и пьезометрической поверхностью.

При вращении сосуда с жидкостью вокруг горизонтальной оси наблюдается неравномерное распределение жидкости на стенках сосуда. Равномерность распределения происходит при высоких частотах вращения, т.е. когда центробежные силы, действующие на частицы жидкости, значительно превышают силы тяжести этих частиц, rw²>>g.

С учетом граничных условий r= r₀ и р =р₀ получаем уравнение:

,

определяющее закон распределения давления в объеме жидкости, вращающейся вокруг горизонтальной оси. Распределение давления по торцу имеет вид параболоида вращения с осью, совпадающей с осью вращения цилиндра, поэтому полное усилие на торец сосуда можно определять методом "тела давления". Поверхности равного давления при таком законе распределения давления в объеме жидкости образуют семейство концентрических цилиндрических поверхностей с осью, совпадающей с осью 0х.

Введение. Разбор решенных задач.

В процессе домашней подготовки предлагается провести самостоятельно разбор решенных задач, приведенных в гл.1 учебного пособия "Гидравлика и гидропневмопривод".[1]

Решение типовых задач

Задача 1.1. Как должны соотноситься диаметры поршня D и d, если поршень находится в системе с жидкостью в равновесии при соотношении высот z₂ = 5 z₁. Весом поршня пренебречь.

Решение.

1-й способ решения:

На верхнюю площадку А снизу вверх действует сила Р_А = ρg z₂πD²/4. На нижнее кольцо В сверху вниз действует сила Р_В=ρg(z₂+ z₁) π(D² - d²)/4. При условии равновесия Р_А = Р_В. Отсюда имеем

z₂D²= (z₂+ z₁) (D² - d²),

а с учетом что z₂ = 5 z₁ получаем D/d = .

2-й способ решения:

На круглой площадке диаметром D строим тело давления между ПП и круглой площадкой - цилиндр диаметром D и высотой z₁. Сила численно равна весу тела Р_А = ρg z₂πD²/4 и направлена вверх, т.к. тело давления построена на не смоченной поверхности.

На кольцевой площадке диаметрами D и d строим тело давления между ПП и кольцевой площадкой - цилиндр диаметром D и d высотой (z₂+ z₁). Сила численно равна весу тела Р_В=ρg(z₂+ z₁) π(D² - d²)/4 и направлена вниз, т.к. тело давления построена на смоченной поверхности.

При условии равновесия Р_А = Р_В имеем D/d = .

З адача 1.2. На два плавающих деревянных бревна диаметрами D = 2R и d = 2r и длиной L каждое положен деревянный настил шириной b и весом G так, что он имеет консоли по обеим сторонам, равные c.

Как расположить добавочный груз Р, для чтобы настил держался горизонтально?

Решение.

При горизонтальном положении настила стрела несмоченного кругового сегмента для обоих бревен одинакова. Выразим площади торцов погруженных в воду частей бревен через радиусы R и r и стрелу f :

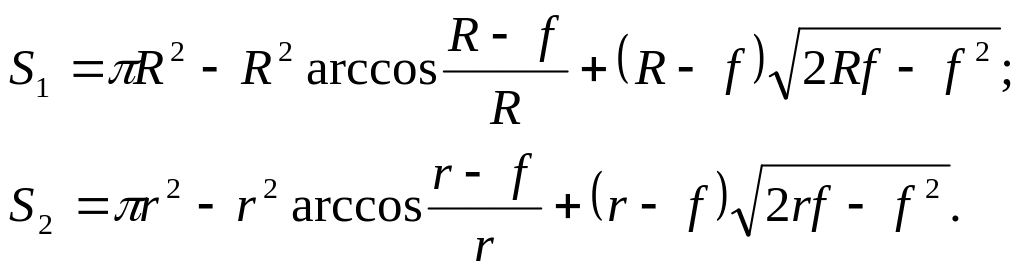(1)

Архимедовы силы, действующие на поплавки (бревна), будут равны

и .(2)

При условии равновесия сумма моментов всех действующих сил относительно любой точки должна быть равна нулю. Сумма моментов относительно левого малого бревна:

. Отсюда имеем (3)

Сумма проекций всех сил на вертикальную ось А₁ + А₂ - Р - G =0 .

При решении уравнений 1, 2 и 3 можно найти стрелу f для конкретных числовых значений R, r, l, ρ, P, G .

Затем при помощи выражений 1 и 2 можно вычислить S₁ и А₁ и, наконец, по 3 вычислить х - искомую величину расположения добавочного груза Р.

З адача 1.3. Цилиндрический сосуд радиуса R = 1 м полностью заполнен водой под давлением, создаваемым столбом воды высотой h = 1 м, и вращается вокруг вертикальной оси с угловой скоростью ω = 8 1/с.

На цилиндрической поверхности сосуда на глубине от верхней крышки имеется квадратный люк с размерами сторон a = 0,25 м.

Определить силы давления на верхнюю крышку и люк, пренебрегая кривизной поверхности люка.

Решение.

В не вращающемся сосуде пьезометрическая поверхность ПП(ω=0) проходит через верхнюю границу расположения жидкости в трубке пьезометра. Сила давления

- на верхнюю крышку определяется по выражению P_кр0= ρghπR² (тело давления показано тонкими вертикальными линиями);

- на квадратный люк P_люк0 = ρgh_С S= ρg(h+H)a², где h_С - координата положения центра тяжести площади квадратного люка от пьезометрической плоскости ПП(ω=0); S - площадь квадратного люка.

Эпюра распределения давления в сосуде показана тонкими линиями.

При вращении сосуда пьезометрическая поверхность ПП(ω≠0) принимает вид параболоида вращения. Высота параболоида вращения определяется по выражению h_пар = ω²R²/2g .

Сила давления на верхнюю крышку определяется по выражению

P_кр= P_кр0 + ρgW_пар = P_кр0 + ρgh_пар πR²/2 = P_кр0 + ρgπω²R⁴/4 g,

где W_пар = h_пар πR²/2 объем тела давления образованное при вращении сосуда с жидкостью, показано толстыми вертикальными линиями;

Сила давления на квадратный люк P = ρgh_С S= ρg(h+H+h_пар)a², где h_С - координата положения центра тяжести площади квадратного люка от пьезометрической плоскости ПП(ω=0); h_пар - высота параболоида на радиусе R; S - площадь квадратного люка.

Задача 1.4. Цилиндрический сосуд радиуса R =0,1 м и высотой h =1 м полностью заполнен водой и вращается вокруг вертикальной оси. В процессе медленного вращения из сосуда выливается жидкость. При достижении сосудом угловой скорости величины ω₁ высота параболоида равна h_пар

= 0,2 м .

Определить во сколько раз надо медленно увеличить угловую скорость вращения сосуда, чтобы в нем осталось половина первоначально залитого объёма жидкости.

Решение.

При вращении сосуда вокруг вертикальной оси в момент касания краев высота параболоида и объём параболоида определяются по выражениям: h_пар = ω²R²/2g и W_пар = h_пар πR²/2. Из приведенных выражений можно заключить, при достижении ω₁ из вращающегося сосуда вылилось 0,1 объёма залитой в цилиндр жидкости, т.е. объем вылившейся жидкости равен

W_ж1=W₁ = h_пар1 πR²/2= πR^{2 .} h_пар1/2= 0,1Н_цил πR².

Для случая оставшейся половины объема жидкости (h_пар0,5 = 0,5Н_цил и W₅ = 5W₁) имеем:

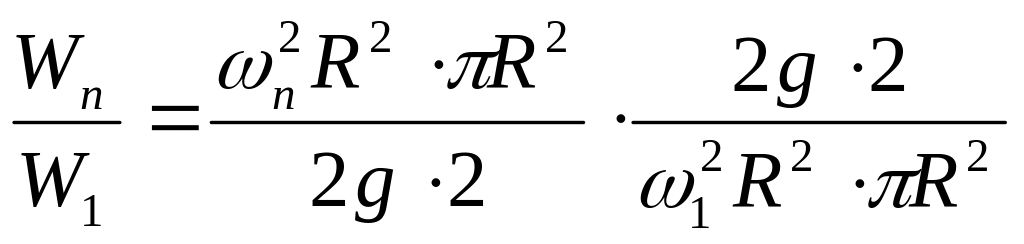или 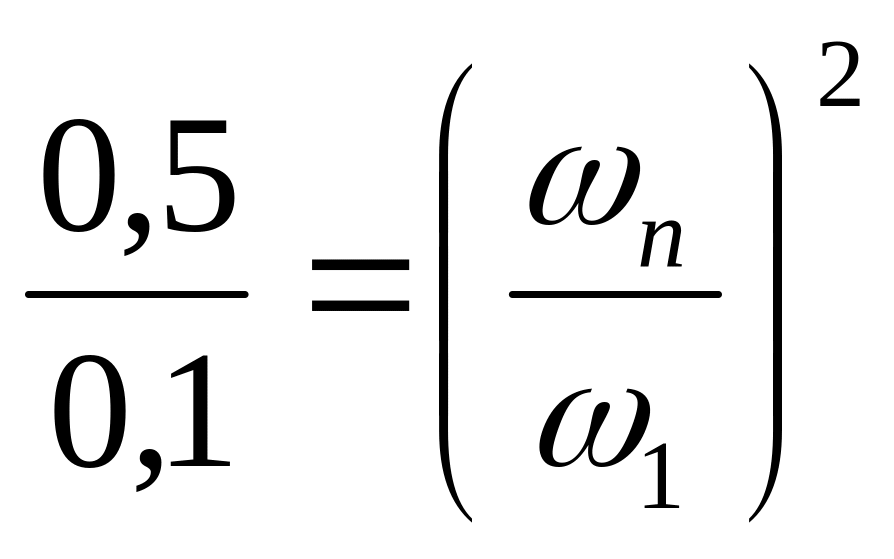. Отсюда имеем .

Задача 1.4. На плоском дне цилиндра установлен сферический клапан радиусом R, перекрывающий канал диаметром d. Определить:

а) силу давления воды на клапан при высоте столба жидкости Н;

б) при какой высоте столба жидкости клапан всплывет, если сила тяжести клапана G?

Решение

Н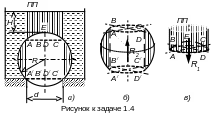 а сферическую поверхность шара действуют горизонтальные и вертикальные силы от окружающей жидкости.

Горизонтальные силы от действия жидкости не оказывают влияния на равновесное состояние шара, так как линии действия элементарных на замкнутую кривую - окружность в горизонтальной плоскости пересекаются в одной точке центре окружности. Суммарная величина равна нулю.

Вертикальные силы образуются от действия жидкости на криволинейную:

- часть сферы шара АВСDE, которая подвергается воздействию переменной высоты столба жидкости от h_ABCD до h_Е (от пьзометрической поверхности ПП до части АВСDEсферы);сила R₁ направлена вниз (рис.1.4, в);

- круговой бочки ABCDA^/B^/C^/D^/, на верхнюю часть которой ABCD - 2R действует переменной высоты столб жидкости h_ABCD до h_2R (от пьзометрической поверхности ПП до части АВСD - 2R сферы), на нижнюю часть диаметр 2R - A^/B^/C^/D^/ действует снизу вверх переменной высоты столб жидкости h_A/B/C/D/ до h_2R (от пьзометрической поверхности ПП до части A^/B^/C^/D^/ - 2R сферы); сила R₂ направлена вверх (рис.1.4, б).

Объем фигуры АВСDE, называемой шаровым сегментом, равен

,

где h_сс - стрелка сегмента; d - диаметр основания (хорда) шарового сегмента; R - радиус сферы (шара).

Стрелка сегмента находится из выражения .

Круговой бочкой ABCDA^/B^/C^/D^/ называют фигуру, образованную вращением дуги окружности сферы вокруг оси сферы. Объем этой фигуры определяют по формуле

,

где Н_КБ = 2R - 2h_сс - высота круговой бочки, имеющей одинаковые торцы диаметром d.

Сегментным поясом назовем фигуру, образованную вращением сегмента вокруг оси шара. Объем этой фигуры определяется по формуле

.

Величина силы, прижимающей шаровой клапан к седлу, определяется по выражению:

.

Величина силы, поднимающей шаровой клапан от седла, определяется по выражению:

.

Полная прижимающая сила равна R_∑ = R₁ + G - R₂ .

Выдача 1-го домашнего задания.

По 1-му заданию выполняются две задачи:

- одна задача из 2-3 главы;

- вторая задача из 4-й главы

из "Сборника задач по машиностроительной гидравлике" Под ред. И.И. Куколевского и Л.Г. Подвидза. МГТУ им. Н.Э. Баумана, 2009г.[]

Отчет о выполнении 1-го домашнего задания оформляется компьютерно на листах формата А4 и должен содержать:

- титульную часть, в которой указывается название темы работы и номера задач, группу и фамилию студента, Ф.И.О. ведущего занятия преподавателя;

- решение задач с подробным изложением порядка решения и выполнением расчетов до третьей значащей цифры.

Защита домашнего задания проводится в виде собеседования с ведущим преподавателем. На выполненном задании и в журнале делается отметка о защите.