775

3. ДИНАМИКА

Задания Д1У и Д2У

Привести краткий (примерно на 1–2 стр.) конспект, включающий ответы на следующие вопросы:

− законы механики Галилея-Ньютона; –дифференциальные уравнения движения материальной точки в декартовых координатах (в

форме Лагранжа) и в проекциях на естественные оси координат (в форме Эйлера);

–механическая система, ее масса; центр масс, силы, действующие на систему;

–моменты инерции системы и твердого тела относительно центра, оси, плоскости; радиус инерции;

–элементарная работа, работа и мощность постоянной и переменной силы;

–кинетическая энергия при поступательном, вращательном и плоском движении твердого тела, теорема об изменении кинетической энергии материальной точки и системы;

–принцип возможных перемещений;

–общее уравнение динамики.

Указания. При выполнении задания Д1У применить теорему об изменении кинетической энергии.

Краткая теоретическая справка

Теорема об изменении кинетической энергии

Теорему об изменении кинетической энергии можно представить как в дифференциальной, так и интегральной форме. В первом случае она формулируется следующим образом: производная по времени от кинетической энергии T равна мощности всех внешних и внутренних сил, действующих на систему:

где Wke, Wki — мощности внешних и внутренних сил; k — индекс силы. Выражение (3.1) можно представить в несколько ином виде:

где dAke и dAki — элементарные работы равнодействующих внешних и внутренних сил, приложенных к точке.

Проинтегрировав обе части равенства в пределах перемещения системы, получим уравнение, выражающее теорему об изменении кинетической энергии механической системы в интегральной форме:

согласно которой изменение кинетической энергии механической системы при ее некотором перемещении равно алгебраической сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.

Для неизменяемой системы, в которой расстояние между точками приложения внутренних сил не изменяется (тела считаются абсолютно твердыми, нити нерастяжимыми, а связи идеальными), сумма работ внутренних сил равна нулю. Тогда:

При поступательном движении твердого тела кинетическая энергия определяется по формуле

где m — масса тела; v — скорость любой его точки.

В случае вращательного движения тела относительно неподвижной оси его кинетическая энергия определяется по формуле

где Jz — момент инерции тела относительно оси вращения; ω — угловая скорость вращения тела.

60

В общем случае движения механической системы или тела кинетическая энергия складывается из кинетической энергии поступательного движения со скоростью центра масс C и кинетической энергии вращательного движения относительно оси, проходящей через центр масс:

22

Работой называется скалярное произведение вектора силы на вектор перемещения. Элементарной называется работа силы на бесконечно малом перемещении:

dA = F cosαds ,

где α — угол между направлением вектора силы и касательной к траектории точки; ds — бесконечно малое перемещение.

При конечном перемещении точки из положения М0 в положение М1 работа силы вычисляется как интегральная сумма элементарных работ:

Работа постоянной силы на конечном прямолинейном перемещении определяется произведением модуля силы на модуль перемещения и на косинус угла между их направлениями:

Работа силы тяжести не зависит от траектории тела, а зависит лишь от изменения высоты его положения:

Если сила приложена к телу, вращающемуся вокруг неподвижной оси, то ее работа равна:

где Mz (F ) — момент силы F относительно оси вращения. При постоянном моменте

где φ — конечный угол поворота тела.

Задача для самоконтроля

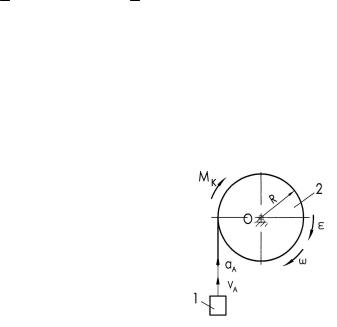
Задача 3.1. Груз 1 массой m (рис. 3.1) прикреплен к тросу, намотанному на барабан 2, к которому приложен постоянный вращающий момент МК. Известны момент инерции барабана относительно оси вращения J, радиус R.

Рис. 3.1

Определить:

−кинетическую энергию системы при скорости груза v;

−работу при подъеме груза на высоту h.

Записать общее уравнение динамики.

Общее уравнение динамики

Согласно принципу Даламбера, если в любой момент времени к телу или системе движущихся тел, к которым приложены активные силы и реакции связей, добавить силы инерции, то можно

61

считать, что система в данный момент времени находится в равновесии. Согласно принципу возможных перемещений для системы, находящейся в равновесии, сумма работ всех активных сил на виртуальных (возможных) перемещениях равна нулю. Если объединить оба принципа, то можно считать, что во всякой механической системе с идеальными связями сумма элементарных работ всех активных сил и сил инерции на виртуальных перемещениях равна нулю. Уравнение, отражающее этот принцип, называют общим уравнением динамики.

Общее уравнение динамики имеет вид:

где ∑δAai, ∑δAui — суммы элементарных работ активных сил и сил инерции. Уравнение (3.18) можно записать также в виде:

где Fi — активные силы; miai — силы инерции равные произведению массы на ускорение с обратным знаком; δsi — возможные перемещения.

Задание Д1У

Применение теоремы об изменении кинетической энергии механической системы

Схема механизма, а также размеры шкивов выбираются из вариантов рисунков и табличных значений к заданию К1У.

Механическая система приходит в движение из состояния покоя под действием сил тяжести. Система содержит ступенчатые шкивы 1 и 2, смонтированные на осях О1, О2. Массы грузов A, А1, B, C: mA = 400 кг, mA1 = 150 кг, mВ = 100 кг и mС = 50 кг. Для вариантов 27, 40, 57, 58, 87 один из грузов выполнен в виде сплошного цилиндра, наружный диаметр которого равен 2r2. Размеры шкивов приведены в табл. К1.1. Массы систем шкивов в табл. Д1.1. Радиусы инерции относительно осей, проходящих через центры тяжести: ρ1 = r1 и ρ2 = r2 .

Коэффициент трения скольжения грузов по наклонным поверхностям f = 0,2. Моменты сопротивления вращению валов в опорах О1, О2 считаем постоянными и равными МС1 = МС2 = МС = 30 Н·м.

Определить скорости грузов в момент, когда груз А переместится на расстояние h. Необходимые для решения исходные данные выбрать из табл. Д1.1.

Нити, которые связывают элементы механической системы, следует считать невесомыми и нерастяжимыми, а их наклонные участки параллельными соответствующим наклонным плоскостям.

Указание. При выполнении задания Д1У применить теорему об изменении кинетической энергии.

62

Пример

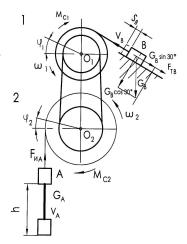
Механическая система (рис. 3.2) приходит в движение из состояния покоя под действием сил тяжести. Система содержит ступенчатые шкивы 1 и 2, смонтированные на осях О1, О2, массы шкивов m1 = 600 кг, m2 = 900 кг; радиусы инерции относительно горизонтальных осей, проходящих через центры тяжести: ρ1 = 0,3 м и

ρ2 = 0,4 м. Массы грузов А, В: mА =

= 400 кг, груза В mB = 100 кг. Коэффициент трения скольжения груза по наклонной поверхности f = 0,2. Моменты сопротивления при вращении валов в опорах О1, О2 считаем постоянными и равными: МС1 = МС2 = МС = 30 Н·м. Радиусы шкивов 1, смонтированных на оси

О1, R1 = 0,5 м, r1 = 0,2 м; радиусы шкивов 2: R2 = 0,6 м, r2 = 0,4 м.

Определить скорости грузов после того, как груз А опустится на высоту h =10 м.

При решении учитываются трение скольжения при перемещении груза по наклонной плоскости и моменты сопротивления вра- Рис. 3.2 щению валов.

Решение

Применим к решению задачи общее уравнение динамики. Поскольку система приходит в движение из состояния покоя, направления ускорений тел соответствуют направлениям их движения.

Силы трения направлены в сторону, противоположную направлению движения. Если направление движения системы выбрано ошибочно, то искомое ускорение получается со знаком минус. В этом случае необходимо изменить направления силы трения и сил инерции и внести соответствующие поправки в общее уравнение динамики.

1. Применим теорему об изменении кинетической энергии механической системы (3.4): T − T0 = ∑Akе .

Кинетическая энергия системы, содержащей грузы А, В, и шкивов 1 и 2:

Кинетическая энергия в начальный момент времени, когда скорости всех тел равны нулю:

T0 = 0.

2. Определим кинетическую энергию системы.

Грузы А, В движутся поступательно. Кинетическая энергия грузов:

где vA, vB — скорости, mА, mB — массы грузов. Шкивы совершают вращательное движение:

63

J1 = m1ρ12; J2 = m2 ρ22,

где J1 и J2 — моменты инерции; ρ1,ρ2 — радиусы инерции шкивов. Кинетическая энергия (3.13):

3. Выразим скорости ω1 , ω2 ,vB через vA . Угловая скорость шкивов 2:

ω2 = vA / R2 .

Шкивы 2 кинематически связаны со шкивами 1 с помощью ременной передачи. Радиусы шкивов r2 иr1. Линейные скорости ремня и точек, находящихся на наружной поверхности шкивов, равны:

ω1 r1 = ω2 r2 .

Угловая скорость шкивов 1:

ω1 = ω2 r2 / r1 = vA r2 / r1 R2 = vA i/ R2 ,

где i = r2/r1.

Линейная скорость груза В:

vB = ω1 R1 = vA i R1 / R2 = vA i iR,

где iR = R1/R2.

Запишем выражение для кинетической энергии (3.14) через скорость vA :

где АА, АВ — работа при опускании груза А и подъеме груза В; АТ — работа силы трения груза В; АМ1, АМ2 — работа моментов сопротивления при вращении шкивов 1, 2.

Работа при опускании груза А на h:

АА = hmAg. Работа при подъеме груза В:

АВ = mВg sin30° sВ,

где sВ — перемещение груза В по наклонной поверхности; mВg sin30° — составляющая веса груза в направлении, обратном перемещению.

Сила трения по закону Кулона:

FТ = fNB = fmB g cos30° ,

где NB — сила нормального давления груза В на опорную поверхность; f — коэффициент трения.

Работа силы трения:

АТ = mВgf cos30° sВ.

Работа моментов сопротивления вращению шкивов:

АМ1 = МС1φ1; АМ2 = МС2φ2,

где МС1, МС2 — моменты сопротивления вращению шкивов 1 и 2; φ1, φ2 — углы поворота шкивов при перемещении груза А на h.

Работа внешних сил (3.18):

64

∑Ake = mAgh − (mBsin30o + FB )sB − MC1ϕ1 −MC2ϕ2 .

5.Выразим перемещение груза В − sB и углы поворота шкивов — ϕ1 , ϕ2через h. Перемещения связаны между собой так же, как соответствующие скорости vB = iiR vA, ω2 = vA / R2 :

sB = hiiR, ϕ2 = h/R2; ϕ1 = iϕ2 = ih/R2.

6. Запишем выражение для работы внешних сил через перемещение груза А с учетом того, что

МС1 = МС2 = МС:

∑Ake = mAgh − mBg(sin30° + f cos30° )hiiR – MC(1 + i)h/R2. (3.19)

Тогда уравнение (3.4) согласно (3.17), (3.19) примет вид:

vB = iiR vA = 5,645/0,6 = 9,4 м/c.

Ответ: vА = 5,645 м/с, vB = 9,4083 м/с

Задание Д2У

Общее уравнение динамики

Исходные данные: схема и размеры механизма выбираются из вариантов рисунков к заданию К1У, массы шкивов и грузов, а также остальные исходные данные соответствуют заданию Д1У. Механическая система под действием сил тяжести приходит в движение из состояния покоя.

Найти ускорение груза А, натяжения ветвей нитей и ремней ременной передачи.

Примечание. При выполнении задания Д2У применить общее уравнение динамики.

Пример

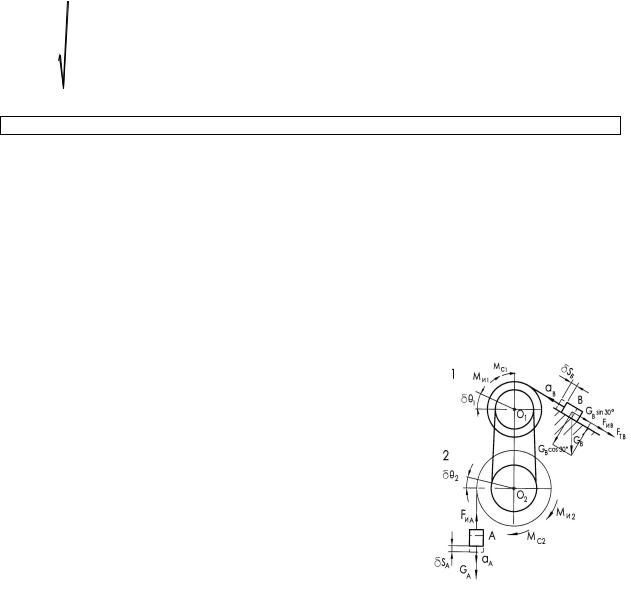
Механическая система показана на рис. 3.3. Под действием сил тяжести она приходит в движение из состояния покоя. Система содержит ступенчатые шкивы 1 и 2, смонтированные на осях О1, О2. Шкивы связаны ременной передачей.

Массы шкивов m1 = 600 кг, m2 = 900 кг; радиусы инерции относительно горизонтальных осей, проходящих через центры тяжести: ρ1 = 0,3 м и ρ2 =

=0,4 м. Массы грузов А, В: mА =

=400 кг, mB = 100 кг. Коэффициент трения скольжения груза по наклонной поверхности f =

=0,2. Моменты сопротивления при вращении валов в опорах О1, О2 считаем постоянными и равными: МС1 = МС2 = МС =

=30 Н·м. Радиусы ступенчатых шкивов 1: R1 = 0,5 м, r1 = 0,2 м; радиусы ступенчатых шкивов 2: R2 = 0,6 м, r2 = 0,4 м.

Найти ускорение груза А, натяжения ветвей нитей и ремней ременной передачи.

Решение

1. Активные силы и силы инерции показаны на рис. 3.3. Там же показано направление движения. Рис. 3.3

2. Кинематические уравнения.

65

Так как система имеет одну степень свободы, перемещения, скорости и ускорения ее элементов однозначно определяются перемещениями, скоростями и ускорениями одного из них, например, груза А.

Будем считать, что груз А под действием силы тяжести перемещается вниз с ускорением аА, а его возможное перемещение δsA.

Центры тяжести шкивов 1 и 2 неподвижны. Угловые скорости ω1, ω2 и ускорения ε1, ε2 шкивов определяются из соотношений:

ω2 = vA/R2; ω1 = i ω2; ε2 = аА/R2; ε1 = i ε2, где vA — скорость груза; i = r2/r1.

Груз В перемещается вверх по наклонной плоскости с ускорением аВ:

аВ = ε1R1 = iε2R1 = аАiiR; iR = R1 /R2.

Зависимости между возможными перемещениями такие же, как между соответствующими скоростями:

где δθ2, δθ1 — углы поворотов шкивов 1, 2; δsВ — перемещение груза В. 3. Определение силовых факторов.

Движение системы происходит под действием силы тяжести груза А:

GA = mAg.

Сила инерции груза А, который движется поступательно с ускорением аА,

FИА = mAаА

направлена противоположно направлению аА.

При опускании груза А шкивы вращаются против часовой стрелки, в эту же сторону направлены угловые ускорения, а моменты касательных сил инерции МИ1 и МИ2 так же, как и моменты сопротивления МС1, МС2, — в противоположную сторону:

МИ1 = J1ε2; МИ2 = J2ε2,

где моменты инерции J1 = m1ρ12; J2 = m2ρ22.

Груз В перемещается вверх по наклонной плоскости. Составляющая веса груза GВ = mВg направлена параллельно опорной плоскости в сторону, противоположную направлению движения:

FGВ = GВ sin30°.

Так же направлена сила трения, которая равна произведению силы нормального давления на коэффициент трения:

FТВ = GВ cos30° f.

Cила инерции направлена вниз параллельно наклонной плоскости, в направлении, противоположном направлению аВ, и равна:

FИВ = mВаВ.

4. Общее уравнение динамики.

Составим общее уравнение динамики (3.19) с учетом того, что работа центробежных сил инерции и реакций идеальных связей равна нулю:

(GA − FИА)δsA − (МИ2 + МС2)δθ2 − (МИ1 + МС1)δθ1 −

– (FИВ + FТВ + GВ sin30°)δsВ = 0.

После подстановки (3.20) и деления на δsA уравнение имеет вид: mA(g − аА) − [(J2аА + МСR2) + (J1аА + МСR2)(1 + i)]/R22−

− mВ[аАiiR + g(fcos30° + sin30°)] iiR = 0.

Тогда

5. Численное решение.

Определим численные значения моментов инерции шкивов J1, J2 и передаточных отношений i,

iR:

66

J1 = m1ρ12 = 54 кг·м2; J2 = m2ρ22 = 144 кг·м2; i = 2; iR = 5/6.

После подстановки всех численных значений в уравнение получим: аА = 1,59 м/с2.

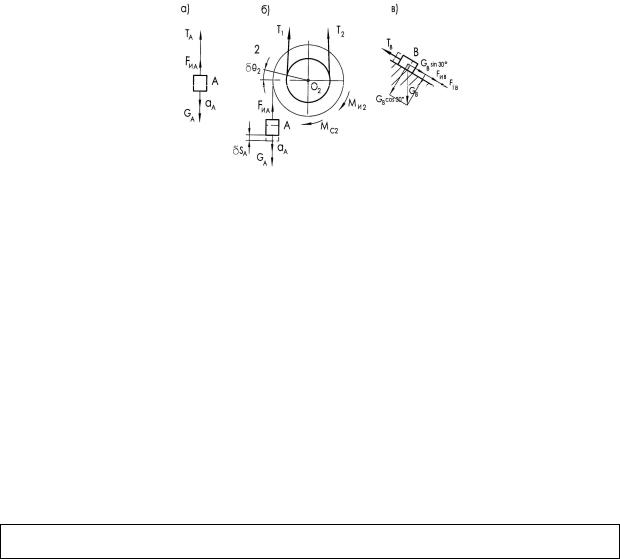
6. Натяжение нитей.

Для определения натяжения нити, на которой подвешен груз, мысленно разрежем нить и заменим ее действие на груз А реакцией ТА (рис. 3.4, а). Используя принцип Даламбера, приравняем нулю проекции всех сил, включая силы инерции, на ось, которая совпадает с осью нити, найдем силу ее натяжения ТА:

ТА = mA(g − аА) = 3,29 кН.

Рис. 3.4

Для определения разности натяжения ветвей ремня ременной передачи мысленно разрежем этот ремень (рис. 3.4, б). Разность натяжения ветвей ремня Т1 и Т2 создает момент относительно оси О2:

МР2 = (Т1 − Т2)r2.

Составим общее уравнение динамики для отсеченной части:

(GA− FИА)δsA − (МИ2 + МС2 + МР2)δθ2 = 0.

После подстановки зависимостей (3.20) и деления на δsA уравнение имеет вид: МР2 = ТАR2 − МИ2 − МС2 = 1,56 кН·м;

(Т1 − Т2) = МР2/r2 = 3,9 кН. Момент относительно оси О1:

МР1 = (Т1 − Т2)r1 = МР2/i = 0,78 кН·м.

Определим натяжение нити, связывающей груз В со шкивами 1 (рис. 3.4, в). Используя принцип Даламбера, получим:

ТВ = mВ[g(sin30° + f cos30°) + аВ] = 0,925 кН, где ТВ — натяжение нити; аВ — ускорение груза В.

аВ = аАiiR = 2,65 м/с2.

Ответ: аА = 1,59 м/с2; аВ = 2,65 м/с2; ТА = 3,29 кН; (Т1 − Т2) = 3,9 кН; ТВ = 0,925 кН.

ОТВЕТЫ К ЗАДАЧАМ ДЛЯ САМОКОНТРОЛЯ

Задача 1.1, а (рис. 1.1, а)

Проекции равнодействующей на оси X, Y: ∑FX = −2 Н; ∑FY = 6,196 Н.

Модуль равнодействующей:

R = 6,51 Н. Главный момент относительно точки О:

∑mO = −246 Н·см.

67

Задача 1.1, б (рис. 1.1, б)

∑FX = −2,44 Н; ∑FY = 0,293 Н; R = 2,46 Н; ∑mO = 17,6 Н·см.

Задача 1.2, а (рис. 1.2, а)

Проекции равнодействующей на оси X, Y:

∑FX = −0,5145 Н; ∑FY = 0; ∑FZ = 2,8575 Н. Модуль равнодействующей:

R = 2,903 Н.

Моменты относительно осей X, Y, Z:

∑mX = 11,43 Н·см; ∑mY = − 8,57 Н·см; ∑mZ = 2,06 Н·см. Главный момент относительно точки О:

∑mO = 14,4 Н·см.

Задача 1.2, б (рис. 1.2, б)

Проекции равнодействующей на оси X, Y:

∑FX = −1,27 Н; ∑FY = −2,7 Н; ∑FZ = 2,12 Н. Модуль равнодействующей:

R = 3,66 Н. Моменты относительно осей X, Y, Z:

∑mX = 13,5 Н·см; ∑mY = − 6,36 Н·см; ∑mZ = −3 Н·см. Главный момент относительно точки О:

∑mO = 15,2 Н·см.

Задача 2.1 (рис. 2.1)

По условию задачи требуется определить скорость и ускорение точки при вращении барабана и опускании груза согласно уравнению x = 2t2 + 4t , м, и разматывании троса. Радиус барабана R = 0,2 м. Скорость и ускорение точки М требуется определить при t1 = 2 с.

Решение

Скорость груза равна скорости точки М барабана:

Угловое ускорение ε = dω = 20 c−2 . При t1 = 2 c: ω = 60 с-1, dt

vM = 12 м/с; an = ω2R = 602·0,2 = 720 м/с2; aτ = εR = 20·0,2 = 4 м/с2.

Ускорение в точке М:

aM = an2 + a22 = 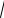7202 + 42 ≈ 720 м/с2

Задача 2.2

Угол поворота: φ3 = −31 рад.

Задачи 2.3 (рис. 2.4, а, б, в)

По условию задачи требуется для заданного положения механизма (рис. 2.4, а, б, в) определить: координаты мгновенного центра скоростей шатуна АВ, угловые скорости звеньев, а также линей-

68

ные скорости и ускорения узловых точек. Угловая скорость кривошипа ОA ω = 4 рад/с, ОA = 0,25 м.

Положение мгновенных центров скоростей показано на рисунке.

X

Задача 2.3 (рис. 2.4, а)

Координаты мгновенного центра скоростей шатуна АВ длиной 0,5м (см. рисунок, а):

XP = 1,116 м; YР = 0. Угловая скорость и ускорение шатуна АВ:

ω1 = 1,155 рад/с; ε1 = 19,55 рад/с2. Скорость и ускорение точек А, В:

vА = 1 м/с; аА = 4 м/с2;

vB = 1,155 м/с; аBАn = 0,67 м/с2; аBАτ = 9,78 м/с2; аBn = 5,33 м/с2; аBτ = 2,31 м/с2; аB = 5,81 м/с2.

Задача 2.3 (рис. 2.4, б)

Координаты мгновенного центра скоростей шатуна АВ длиной 0,433 м (см. рисунок, б):

XP = 0,866 м, YР = 0, 5 м. Угловая скорость и ускорение шатуна АВ:

ωAB = 1,33 рад/с; εAB = 8,2 рад/с2. Скорость и ускорение точек А, В:

VА = 1 м/с; аА = 4 м/с2; vВ= 1,155 м/с; аВАn = 0,77 м/с2; аВАτ = 3,55 м/с2; аВ = 0,9 м/с2.

Задача 2.3 (рис. 2.4, в)

Угловая скорость и ускорение шатуна АВ длиной 0,5 м (см. рисунок, в): ω1 = 0; ε1 = 9,2 рад/с2.

Скорость и ускорение точек А, В:

vА = 1,0 м/с; аА = 4 м/с2;

vB = 1,0 м/с; аBАn = 0; аBАτ = 4,6 м/с2; аB = 2,3 м/с2.

Задача 3.1 (рис. 3.1)

Кинетическая энергия системы при скорости груза v: Т = v2(m + J/R2)/ 2.

Работа при подъеме груза на высоту h:

A = МКh/R − mgh. Общее уравнение динамики:

(МК − εJ)δθ − m(g + а)δs = 0; или, так как δθ = δs/R,

(МК − аJ R)/R − m(g + а) = 0,

69