
Kinematika_slozhnogo_dvizhenia_tochki
.pdf
Московский государственный технический университет имени Н.Э. Баумана
КИНЕМАТИКА СЛОЖНОГО ДВИЖЕНИЯ ТОЧКИ
Издательство МГТУ им. Н.Э. Баумана
Московский государственный технический университет имени Н.Э. Баумана
КИНЕМАТИКА СЛОЖНОГО ДВИЖЕНИЯ ТОЧКИ
Методические указания к курсовой работе по теоретической механике
М о с к в а Издательство МГТУ им. Н.Э. Баумана
2 0 0 7
УДК 539.3 ББК 22.21
К16
Рецензент Л.П. Варламова
Кинематика сложного движения точки: Методические К16 указания к курсовой работе по теоретической механике / В.В. Дубинин, Г.М. Тушева, Г.И. Гатауллина, А.В. Ремизов. –
М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. – 52 с.: ил.
Представлены 40 вариантов задач курсовой работы по курсу теоретической механики на тему «Кинематика сложного движения точки», четыре примера решения типовых вариантов.
Для студентов 1-го курса.
Ил. 26.
УДК 539.3 ББК 22.21
© МГТУ им. Н.Э. Баумана, 2007
ВВЕДЕНИЕ
Студент в выданном варианте курсового задания получает схему механической системы (механизма), описание схемы (с указанием номера варианта задания) и общие условия, в которых указывается, что необходимо определить в задании (контрольные вопросы вариантов).
На схеме варианта курсового задания положение механической системы (механизма) указано в момент времени t = 1 c в неподвижной системе координат x1 y1z1. Положение точки М при t = 1 c
студент определяет в подвижной системе координат с помощью закона относительного движения M0M = f (t), где M0 , M – на-
чальное и текущее положения точки М. Заданные законы движения механизма справедливы на расчетном отрезке времени, включающем момент времени t = 1 c.
В большинстве вариантов заданий системы совершают движение в плоскости чертежа. В вариантах 7, 27, 28, 30, 31 системы пространственные.
Использование ЭВМ при расчетах курсовых заданий согласуется с преподавателем.
Размерность в законах движений линейных величин [S] =м, угловых [ϕ] =рад, [t] =с. Размерность соблюдается следующим образом:
1) S = a +bt +ct2 + dekt+k1 + a rt2 |
, где |
[S] =[r] = м, тогда |
1 |
|
|
[a] =[d ] =м, [b] =м/с, [c] = м/с2, [k] = с–1, [k ] = 0 |
(безразмерная вели- |
|
чина), [a ] = с–2; |
1 |
|
|
|
|
1 |
|
|
2) ϕ =b1t +c1t2 , где [ϕ] =рад, [b1] = рад/с, [c1] = рад/с2.
Пример. Если S = 0,1(6t −t2 ), то b = 0,6 м/с, с = –0,1 м/с2. Если
ϕ= 4t −t2 , то b1 = 4 рад/с, c1 = –1 рад/с2.
Вкаждом варианте курсового задания, рассматривая движение точек М и D как сложное, студент решает для точки М «прямую» задачу, а для точки D – «обратную» задачу (см. примеры).
3
1. КОНТРОЛЬНЫЕ ВОПРОСЫ
Для момента времени t = 1 c выполнить следующее. 1. Определить:
ввариантах 1–6, 8, 10–12, 16–19, 21–24, 26–29, 32–33 угловые скорость и ускорение звена, несущего на себе точку М, а также относительное ускорение точки D (по отношению к звену 2);
ввариантах 7, 14, 20 – абсолютные скорость и ускорение точки D и ее относительное ускорение по отношению к звену 2;
ввариантах 9, 15, 25, 30, 31, 34 – угловые скорость и ускорение звена 2 и относительное ускорение точки D по отношению к звену 2;
вварианте 13 – угловые скорость и ускорение звена 2 и отно-
сительное ускорение точки (выступа) D(2) относительно диска 1;
в вариантах 35–40, связав подвижную систему координат, указанную на схеме механизма, с телом 1, – абсолютные, относительные и переносные скорости и ускорения, а также кориолисово ускорение точки D(i) того тела, номер которого i указан при точке.
2.Найти по всех вариантах абсолютные скорость и ускорение точки М.
3.Изобразить на рисунках схем механической системы (механизма) все векторы скоростей и ускорений точек М и D. Направление определяемых угловых скоростей и ускорений звеньев указать на схемах круговыми стрелками.
Внекоторых вариантах задания при точке D индексом i указан номер звена, которому она принадлежит. В ряде вариантов в качестве точки D рассматривается малое кольцо.
Для решения и «прямой», и «обратной» задач для сложного движения точки используются теоремы сложения скоростей и ускорений
|
|
|
|
|
|
|
|
|
|
|
|
|
и a = ar + ae + ak , |
|
|||
|
|
|
|
V |
=Vr +Ve |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
и ae – пе- |
|||||||
где V |
и a – абсолютные, Vr |
и ar – относительные, Ve |
|||||||||||||||
реносные скорости и |
ускорения точки. |
Ускорение |
Кориолиса |
||||||||||||||
|
|
|
|
|
|||||||||||||
ak = 2(ωe ×Vr ), где ωe |
– угловая скорость |
переносного движения. |
|||||||||||||||
4
Методические указания к выполнению курсовой работы и решению задач по теме «Кинематика сложного движения точки» (Дубинин В.В., Гатауллина Г.И., Тушева Г.М. М., 2005) содержат примеры подробного решения разнообразных «прямых» и «обратных» задач и являются основным руководством при выполнении этого курсового задания. Проработав эти методические указания, полезно рассмотреть приведенные ниже примеры решения типовых вариантов данного курсового задания.
2. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ВАРИАНТОВ КУРСОВОГО ЗАДАНИЯ
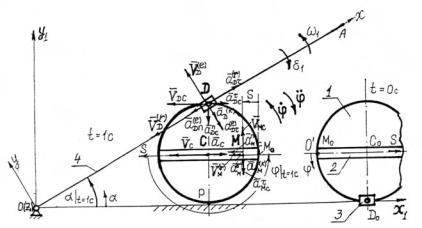
Пример 1. Диск 1 (рис. 1) катится без скольжения по прямолинейной направляющей, закон вращения его имеет вид
ϕ = π2 (3t −t2 ), [t] =c. По пазу 2 на диске движется точка М по за-
кону М0М = S = R(1 – coskt), [t] = c. В точке D диска закреплена шарнирно втулка 3, связанная со стержнем 4, вращающимся во-
круг оси O(z1), [ϕ] =рад, [S] = м.
Рис. 1
1. Определить абсолютные скорость и ускорение точки М, угловые скорость и ускорение стержня и относительное ускорение точки D при t = 1 с.
5

2.Составить уравнения для определения величин, указанных в п. 1, в функции времени; провести расчеты на ЭВМ, построить графические зависимости.
3.Проверить уравнения п. 2 с помощью уравнений кинематики точки.
Принять R = 0, 2 |
м, k = π рад/с, OD =1,32 м =l. |
|
|
|
|||
|
4 |
|
0 |
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. а) Определим положение системы при t = 0 с и t = 1 c. С |
|||||||
помощью законов движения ϕ= |
π |
(3t −t2 ), S = 0, 2 |
|
−cos |
π |
|
|
2 |
1 |
4 |
t по- |
||||
лучим при t = 0 c |
|
|
|
|
|
||
ϕ = 0 рад, S = 0 м, при t = 1 c |
ϕ = π рад, S = |
||||||
= 0,0586 м. Эти два положения изображены на рис. 1. Координаты точки D равны:
|
x1D =l − Rϕ+ R sin ϕ, |
y1D = R(1 −cos ϕ), |
(1) |
|||
при |
t = 1 с ϕ = π рад, x1D = |
l |
– |
πR =1,32 −0,2π = 0,692 |
м, |
|
y |
= 0,2(1 −cos π) = 0, 4 м, OD = |
x2 |
|
+ y2 , OD = 0,8 м, α =30o. |
||
1D |
|
1D |
|
1D |
|
|
б) Будем рассматривать движение точки М как сложное. Неподвижную систему координат Ox1 y1(z1) свяжем с неподвижной
направляющей, подвижную систему M0M = S – с диском 1. Тогда
относительное движение точки М – прямолинейное движение по пазу, переносное – плоское движение диска (движение подвижной системы M0M = S по отношению к неподвижной Ox1 y1(z1)).
Определим абсолютную скорость точки М при t = 1 c с помощью формулы сложения скоростей
|
|
|
|
|
|
|
|
(e) +V |
(r). |
(2) |
|||||||
V |
|
=V |
|||||||||||||||
|
|
M |
|
|
|
M |
|
|
|
M |
|
||||||
Для переносной скорости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(e) =V |
|
|
|
|
, |
(3) |
|||||||||
V |
+V |
||||||||||||||||
|
|
M |
|
|
|
|
C |
|
|
MC |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VMC MC, VC =CP ω, VMC = MC ω= (R − S)ω, ω= ϕ,
6
при t = 1 с |
ω= ϕ= |
π(3 |
−2t) |
|
t=1 c |
= π |
рад/ c > 0, |
V = 0, 2 π |
= |
|||
|
||||||||||||
|
|
|
2 |
|
|
2 |
|
C |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|||
= 0,314 м/с, V |
|
= (0, 2 −0,0586) π |
= 0, 222 м/с. |
|
|
|
||||||
MC |
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Для относительной скорости точки М имеем
VM(rτ) = S = R k sin kt;
VM(rτ) t=1 c = 0, 2 π4 sin π4 t t=1c =0,111 м/с > 0.
Получим ω= ϕ> 0 и S > 0 при
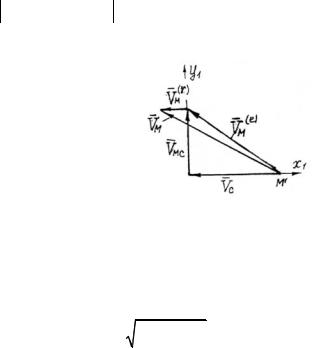
t = 1 c, что означает: круговая стрелка ω диска и вектор относительной скорости направлены в сторону положительного направления отсчета ϕ и S. На рис. 2 построен
многоугольник скоростей для точки М по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(r). |
(4) |
Рис. 2 |
|
V |
|
=V |
+V |
+V |
|||||||||||||
|
M |
|
|
C |
|
|
MC |
|
|
M |
|
|
|
||||
Проекции и модуль абсолютной скорости точки М равны:
|
V |
|
= −V −V (r) , V |
|
= −0,314 −0,111 = −0,425 м/с; |
||||||||||||||
|
Mx |
C |
M |
|
Mx |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
V |
=V |
|
, V |
= 0, 222 м/с; V |
= |
|
V 2 |
|
+V |
2 |
, |
V |
= 0,48 м/с. |
||||||
My1 |
MC |
My1 |
|
|
|
|
|
|
M |
|
|
Mx |
|
My |
|
M |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
Определим абсолютное ускорение точки М: |
|
|
|
||||||||||||||||
|
|
|
|
|
aM = aM(e) + aM(r) |
+ aM(K ) , |
|
|
|
(5) |
|||||||||
где переносное ускорение точки М |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
a (e) = a |
+ a n |
|
+ a τ |
, |
a |
= a n |
+ a τ |
, |
(6) |
|||||||
|
|
|
M |
|
C |
|
MC |
|
MC |
|
C |
|
C |
|
C |
|
|
||
7
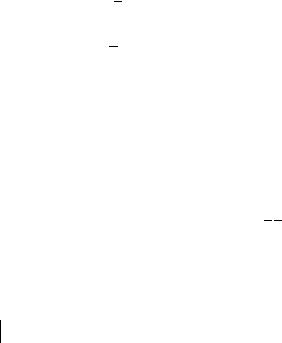
a n = 0, |
так |
как точка С движется |
прямолинейно, |
aτ |
= |
||||
C |
|
|
|
|
|
C |
|
||
= |
dVCτ |
= Rϕ, |
где ε = ϕ, ε = −π ≈ −3,14 |
рад |
, при ϕ< 0 |
проекция на |
|||
dt |
с2 |
||||||||
|
|
|
|
|
an |
|
|||
S касательного ускорения точки С отрицательна (aτ |
< 0); |
= |
|||||||
|
|
|
|
|
C |
|
MC |
|
|
= ω2 MC, aMCτ = ε MC, MC = R − S. Относительное ускорение |
|
||||||||
|
|
|
aM(r)τ = S = R k2 cos kt, |
|
(7) |
||||
ускорение Кориолиса
aM(K ) = 2(ωe ×VM(r) ),
(K ) |
(r) |
n(r) |
). |
где ωe = ω, aM |
= 2ωe VM |
sin(ωe , VM |
При t = 1 c рассчитаем модули векторов ускорений:
aC = aCτ = 0, 2 π = 0,628 м/с2 ; aMCn = π42 (0, 2 −0,0586) = 0,349 м/с2 ; aMCτ = π(0,2 −0,0586) = 0, 444 м/с2 ,
где вектор aMCn направлен от точки М к полюсу С, aMCτ MC и направлен в соответствии с круговой стрелкой ε по отношению к
точке С. Для aM(r) = aMn(r) + aM(rτ) слагаемое aMn(r) = 0, так как относительное движение точки М прямолинейное;
aM(r)τ = S t=1c = 0,2 16π2 cos π4 = 0,087 м/с2 > 0,
вектор aM(r) = aM(r)τ и направлен всторону положительного отсчета S.
Для aM(K ) имеем
aM(K ) = 2 π2 0,111sin 90D = 0,349 м/с2.
8

Направление ускорения aM(K ) получаем по правилу Жуковского поворотом вектора VM(r) на 90° по круговой стрелке ωe = ω. На рис. 3 построен вектор-
ный многоугольник для абсолютного ускорения точки М по формуле
aM = aC + aMCn + aMCτ + aM(r) + aM(K ). (8)
Проекции и модуль |
абсолютного |
Рис. 3 |
||||||
ускорения точки М равны: |
|
|
|
|
|
|||
|
|
a |
Mx |
= a −an |
|
−a(r) , |
|
|
|
|
|
C |
MC |
M |
|
||
|
|
|
1 |
|
|
|
|
|
aMx |
= 0,628 −0,349 −0, 087 = 0,192 м/с2 ; |
|||||||
|
1 |
|
|
|
|
|
|
|
aMy = −aMCτ |
−aM(K ) , aMy = −0, 444 −0,349 = −0,793 м/с2 ; |
|||||||
1 |
|
|
|
1 |
|
|
|
|
a |
M |
= a |
2 |
+ a2 |
, a |
M |
= 0,816 м/с2. |
|
|
Mx1 |
My1 |
|
|
|
|||
Замечание. Переносные скорость и ускорение точки М равны скорости и ускорению точки M ′ диска, с которой в данный момент (t = 1 c) совпадает точка М, поэтому
|
|
|
|
(e) |
(e) |
′ |
|
|
|
||||
VM ′ =VM |
, aM ′ = aM |
, M C = MC. |
||||
в) Будем рассматривать движение точки D как сложное, чтобы определить угловые скорость и ускорение стержня ОА. Неподвижной будем считать систему Ox1 y1(z1), подвижную систему коор-
динат Оху скрепим со стержнем ОА.
Абсолютное движение точки D – движение точки диска, совершающего плоское движение, относительное движение точки D – прямолинейное движение по стержню, переносное движе-
ние ее – вращение стержня 4 вокруг оси О(z1). Запишем для точки D формулу сложения скоростей:
|
|
|
|
|
|
|
(e) +V |
(r). |
(9) |
|||
V |
|
=V |
||||||||||
|
|
D |
|
|
D |
|
D |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9
