отчет лр2

Федеральное государственное бюджетное образовательное учреждение высшего образования «Национальный исследовательский университет «МЭИ»

Лабораторная работа №2

по дисциплине: «Вычислительные методы»

«Решение нелинейных уравнений методом простой итерации»

Студент: Муромцева Эльвира

Группа: А-03-19

Проверил: Крупин Г. В.

Москва

2021

Вариант 11

Цель работы. Изучить и применить на практике метод простой итерации поиска корней функции одной переменной. Познакомиться на практике с понятием сходимости со скоростью геометрической прогрессии. Научиться сравнивать скорость работы итерационных методов.

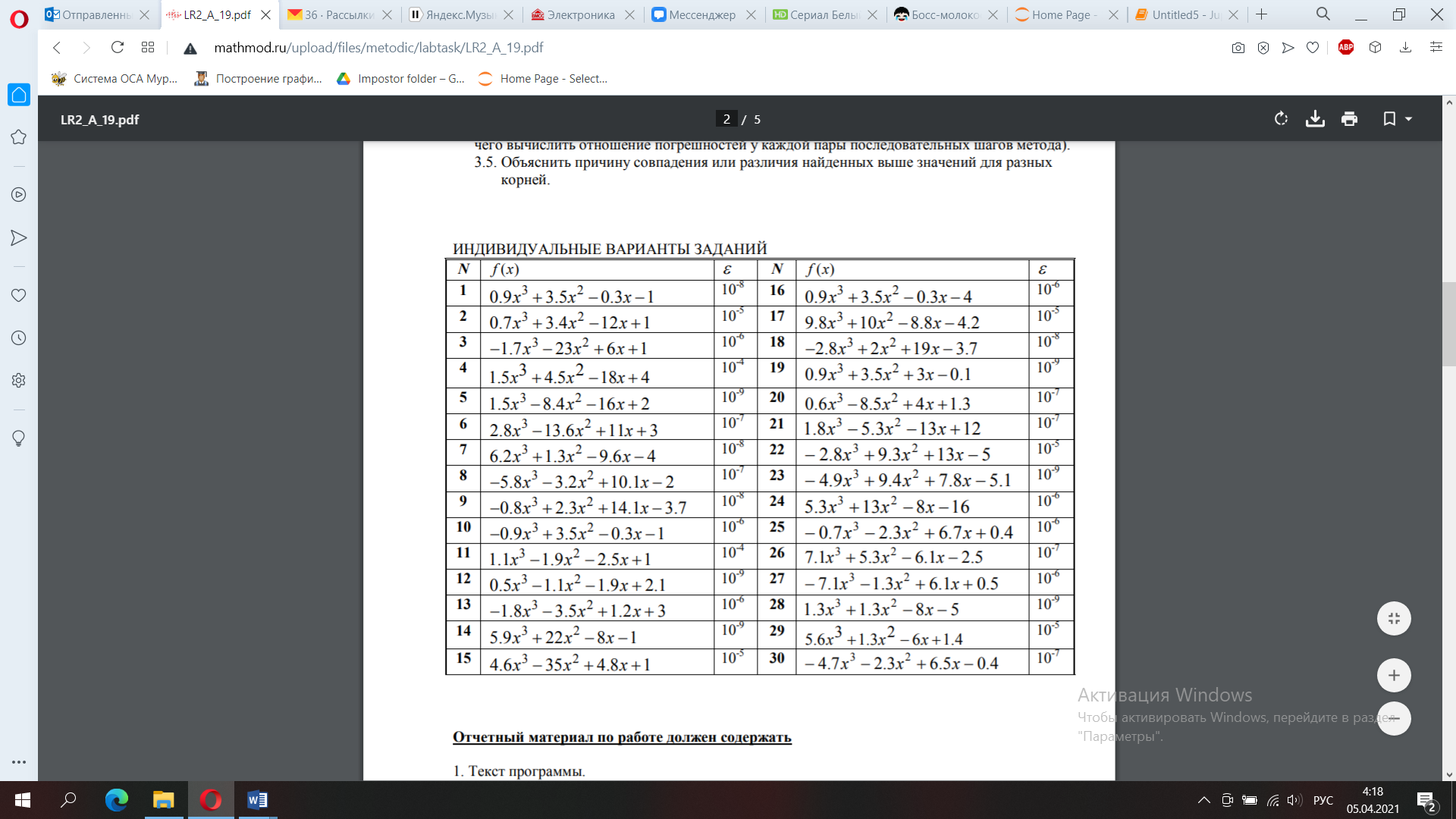
Задача 1

Методом простой итерации найти максимальный вещественный корень уравнения f(x) = 0 с точностью ε.

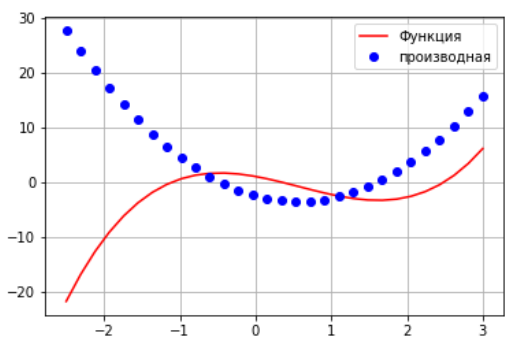
Функция пересекает ось 0У 3 раза.

Протабулируем производную функции и найдем ее максимум и минимум

1. [2.4; 2.6]

2. [0.2; 0.4]

3. [-1.2; -1]

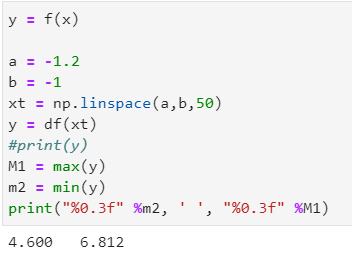
Найдем приближение к корню

1)

2)

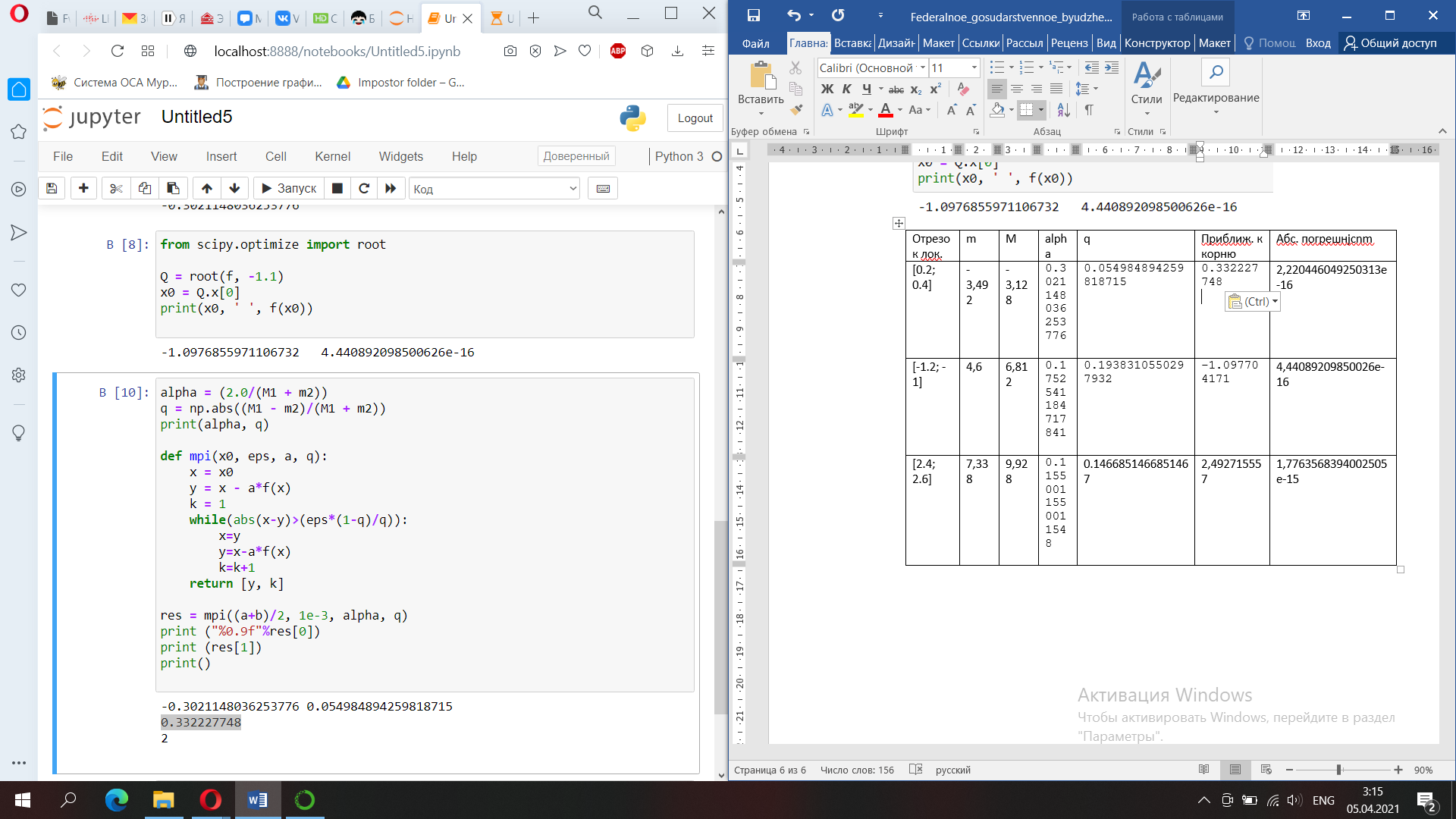
3)

Найдем абсолютную погрешность:

1)

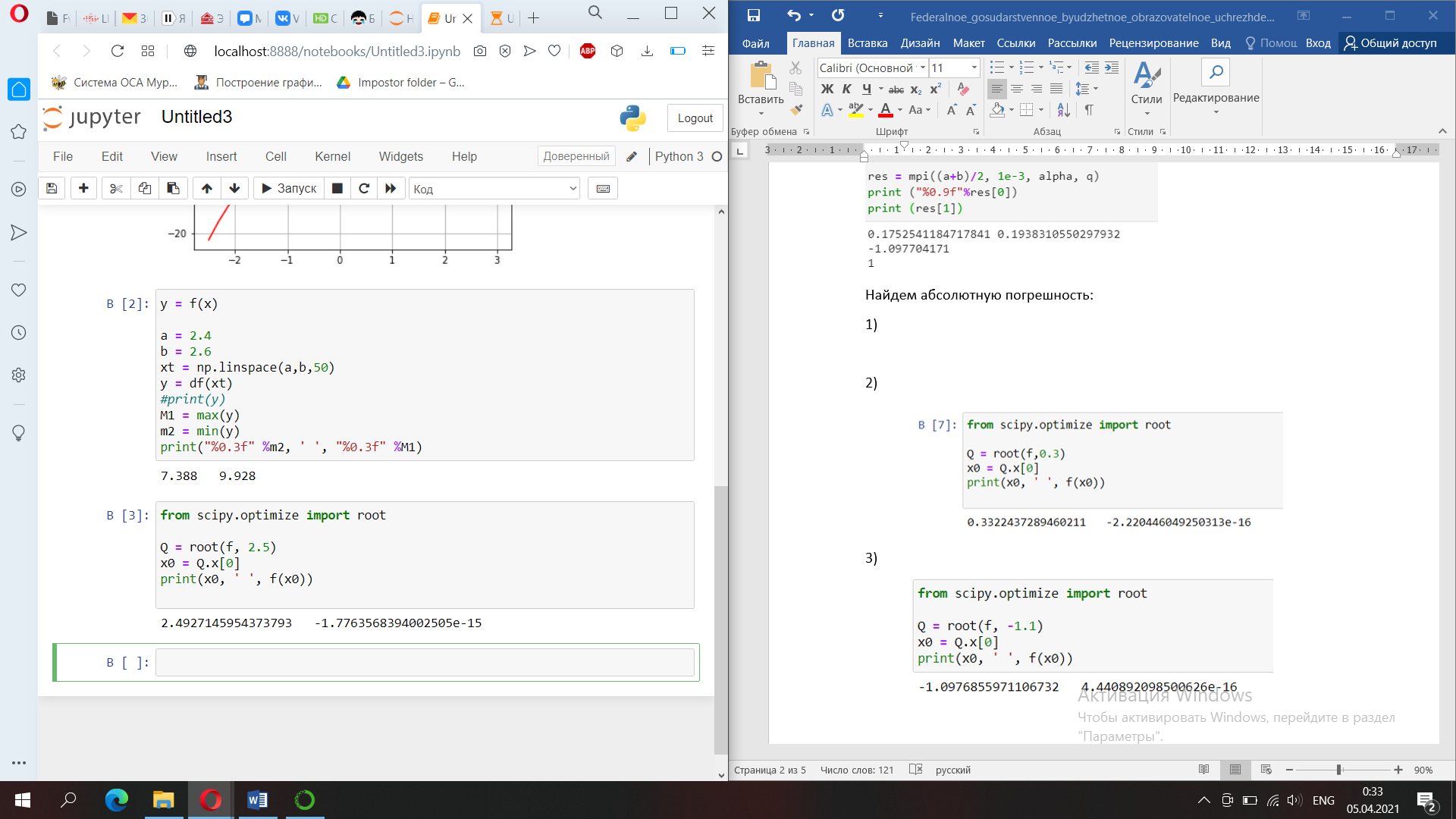
2)

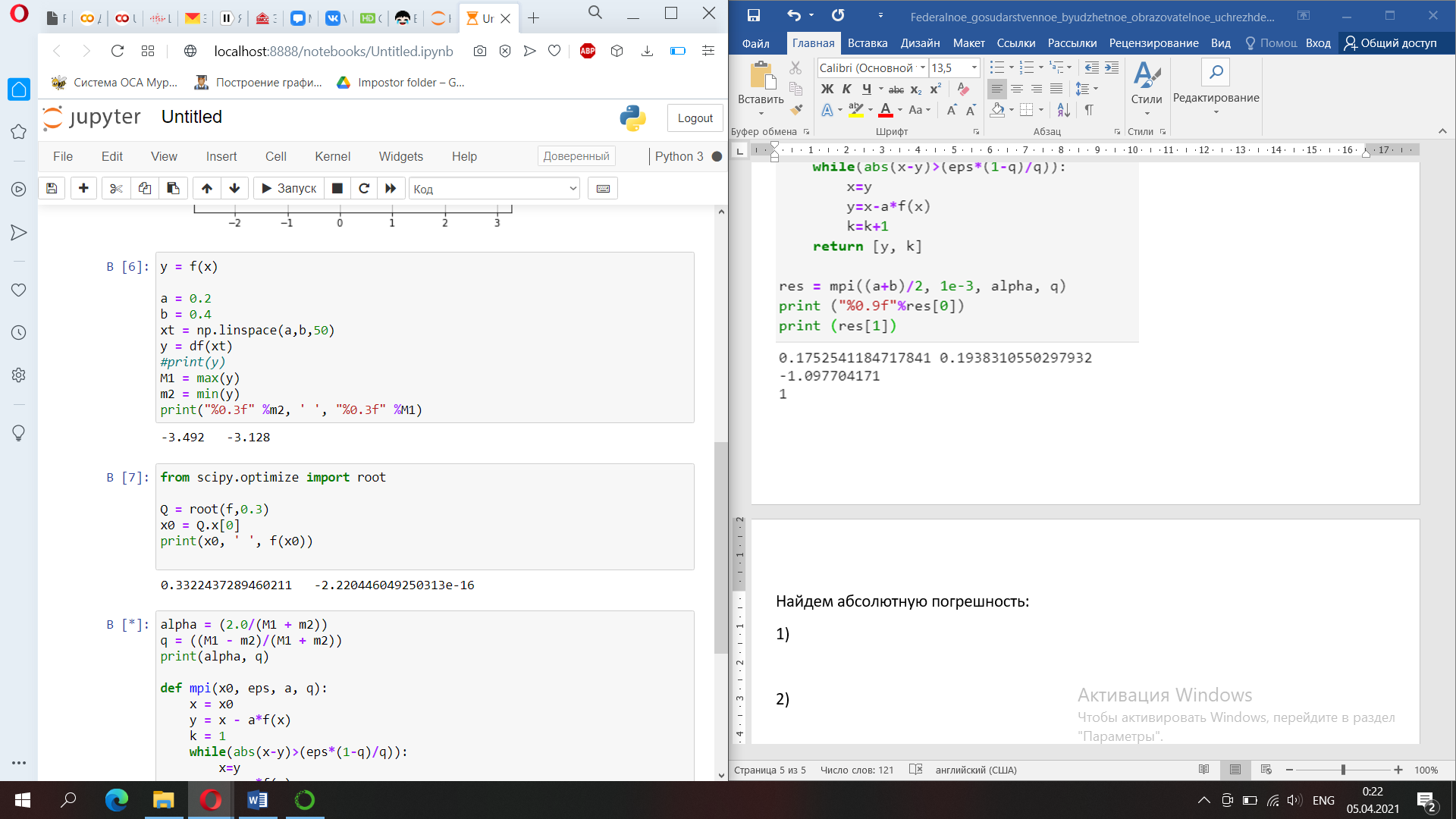
3)

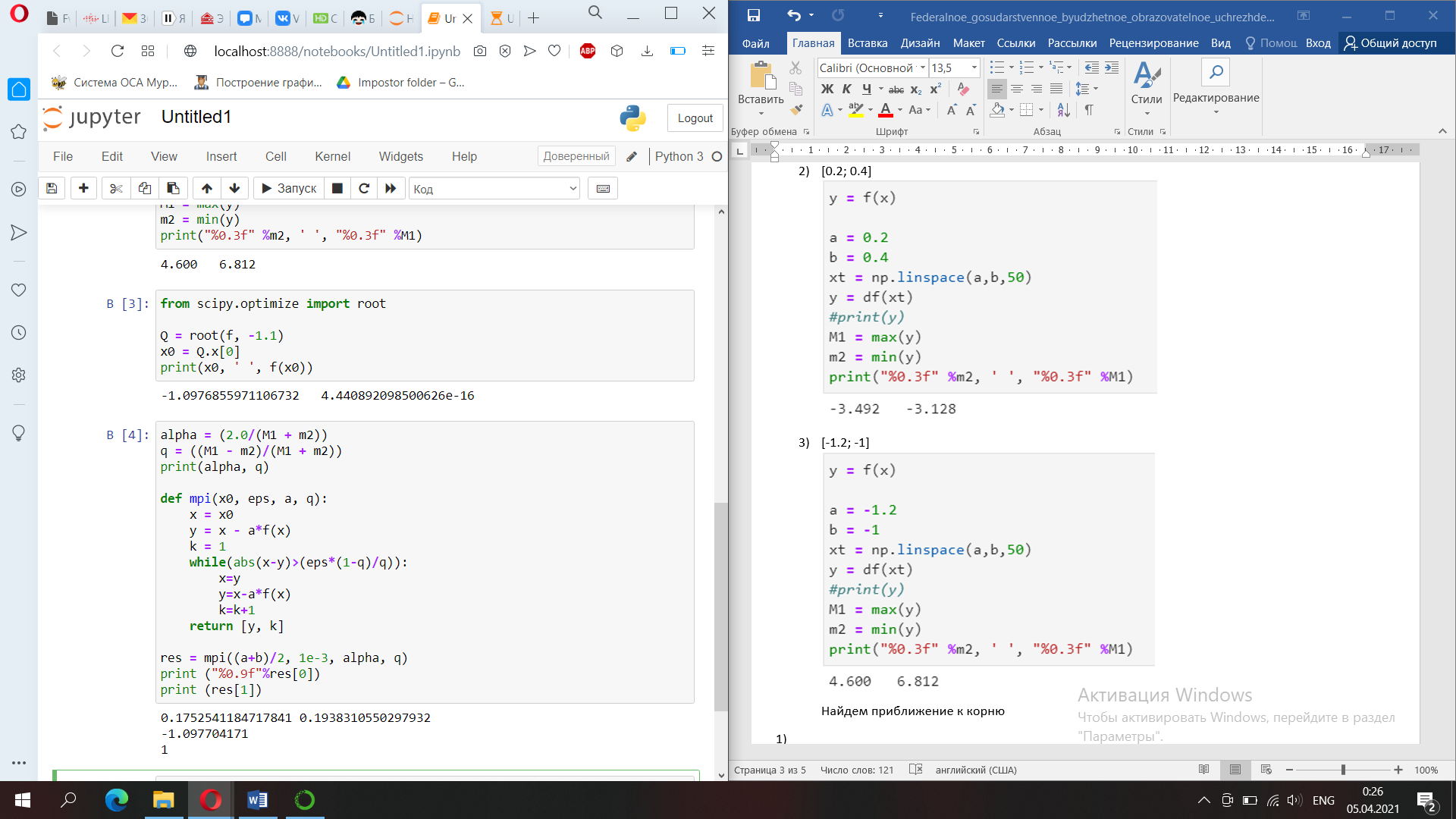
Отрезок лок.	m	M	alpha	q	Приближ. к корню	Абс. погрешнjcnm
[0.2; 0.4]	-3,492	-3,128	0.3021148036253776	0.054984894259818715	0.332227748	2,220446049250313е-16
[-1.2; -1]	4,6	6,812	0.1752541184717841	0.1938310550297932	-1.097704171	4,44089209850026е-16
[2.4; 2.6]	7,338	9,928	0.11550011550011548	0.1466851466851467	2,492715557	1,7763568394002505е-15

Задача 2

Методом простой итерации найти все вещественные корни уравнения из задачи 1 точностью ε = 10-13. Проследить за поведением погрешности, используя апостериорную оценку (на каждой итерации). Объяснить полученные результаты.

Отрезок локализации от -1,2 до -1,0

k = 1 x1 = -1.0974846110592045 0.002370098329692064

k = 2 x1 = -1.0976834946298604 4.781852807509115e-05

k = 3 x1 = -1.097685575521655 5.003187662797422e-07

k = 4 x1 = -1.097685596889033 5.1374609057729535e-09

k = 5 x1 = -1.0976855971083979 5.274291563881291e-11

k = 6 x1 = -1.0976855971106498 5.41453452122507e-13

точность 10**(-13) достигается на 6 итерации

отрезок локализации от 0,2 до 0,4

k = 1 x1 = 0.33222774790814835 3.561633208417292e-05

k = 2 x1 = 0.33224415497766596 9.54631282674236e-07

k = 3 x1 = 0.33224371758692883 2.5449205293318206e-08

k = 4 x1 = 0.3322437292488823 6.785407702821119e-10

k = 5 x1 = 0.33224372893794607 1.809155762824024e-11

k = 6 x1 = 0.3322437289462363 4.823615221373196e-13

точность 10**(-13) достигается на 6 итерации

отрезок локализации от 2,4 до 2,6

k = 1 x1 = 2.4926896916137466 0.0002694227715952068

k = 2 x1 = 2.492714234429667 4.218919358281323e-06

k = 3 x1 = 2.4927145902106576 6.115888709623072e-08

k = 4 x1 = 2.492714595361707 8.854673380251426e-10

k = 5 x1 = 2.4927145954362837 1.2819778325588348e-11

k = 6 x1 = 2.4927145954373633 1.8558036055966267e-13

точность 10**(-13) достигается на 6 итерации

На всех отрезках точность 10**(-13)достигается на 6 итерации

Вывод: Количество итераций необходимое для нахождения корня определенной точности, в моем случае, совпадает на всех трех отрезках. На самом же деле количество итераций зависит от значения q и начального приближения.