
лр4 Cиницин
.docxФедеральное государственное бюджетное образовательное учреждение высшего образования "Национальный исследовательский университет "МЭИ"
ОТЧЕТ
по лабораторной работе № 4
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ
Дисциплина – Вычислительные методы
Вариант 16
Подготовил: студент
Группы А-03-19
Синицин Данил
Москва 2021

Задача 1
Найти приближенное решение задачи Коши для обыкновенного дифференциального уравнения (ОДУ) 1 порядка
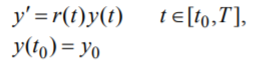
и вычислить и погрешность приближенного решения.
Найти приближенное решение задачи Коши для обыкновенного дифференциального уравнения 1 порядка.

Найти приближенное значение задачи Коши с шагом
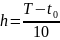 явным методом Эйлера, методом Эйлера-Коши,
усовершенствованным методом Эйлера.
явным методом Эйлера, методом Эйлера-Коши,
усовершенствованным методом Эйлера.

0.1 |
0.10314944111034893 |
0.11289069734329879 |
0.13010259443192515 |
0.15624981989398867 |
0.19338290829137833 |
0.2441382598351195 |
0.3117381692971491 |
0.39999084648627775 |
0.5132904239805517 |
0.6566169558475791 |
0.8355364122609948 |
1.0562006733362268 |
1.325347523771074 |
1.6503006487650898 |
2.038969631157403 |
2.499849949536932 |

0.1 |
0.10311284046692608 |
0.11273870098772823 |
0.1297309272199167 |
0.15550813907803085 |
0.19205485900378766 |
0.2419216945070511 |
0.3082253156274777 |
0.39464839825700615 |
0.5054395999695235 |
0.6454135733540305 |
0.8199510018762668 |
1.0349986435320646 |
1.297069373143781 |
1.6132422190998852 |
1.991162393391232 |
2.4390413153132737 |

0.1 |
0.10307692307692308 |
0.1126849982596589 |
0.12966492950426503 |
0.15542029221401632 |
0.19191786645303813 |
0.24168712889951138 |
0.3078195716036963 |
0.3939681906476511 |
0.5043472095791051 |
0.6437319808723716 |
0.8174589900807756 |
1.0314259066112739 |
1.2920916482787979 |
1.6064764435186374 |
1.9821618849015161 |
2.42729097254895 |

Используя метод Рунге-Кутты 4 порядка точности, найти приближенное решение задачи Коши с тем же шагом.
0.1 |
0.10314944111034893 |
0.11289069734329879 |
0.13010259443192515 |
0.15624981989398867 |
0.19338290829137833 |
0.2441382598351195 |
0.3117381692971491 |
0.39999084648627775 |
0.5132904239805517 |
0.6566169558475791 |
0.8355364122609948 |
1.0562006733362268 |
1.325347523771074 |
1.6503006487650898 |
2.038969631157403 |
2.499849949536932 |

Найти величины погрешностей приближенных решений по формуле:
![]() ,
,
где
y(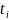 )и
)и
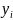 значения точного и приближенного решений
в узлах сетки
.
значения точного и приближенного решений
в узлах сетки
.

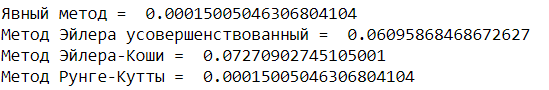
Построить таблицы и графики найденных решений. Сравнить полученные
результаты.
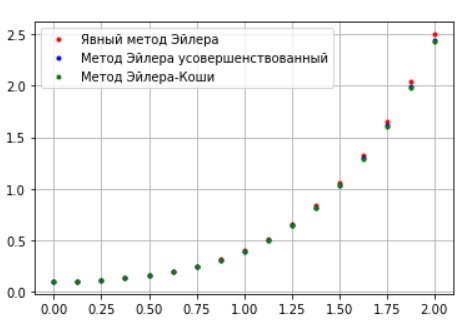
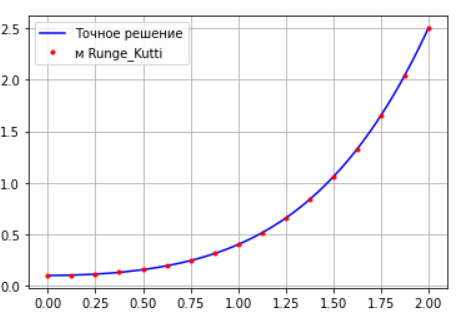
На основе полученных наблюдений можно сделать вывод, что для конкретной
задачи наименее точными являются усовершенствованный метод Эйлера и метод Эйлера-Коши, затем метод Эйлера и метод Рунге-Кутты.
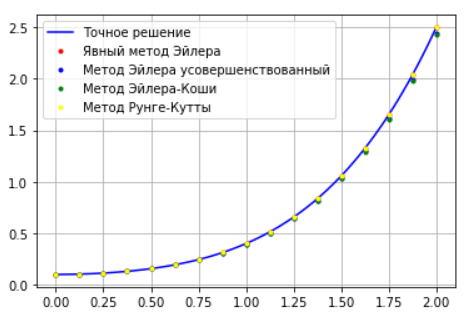
(на данном графике видны не все точки)
Код программы
import math
import numpy as np
import matplotlib as plt
import matplotlib.pyplot as plt
def f(t,y):
return 4*y*t/(1+t**2)
def Yt(t):
return 0.1*(1+t**2)**(2)
#Явный метод Эйлера
def Euler(f,t0,y0,h,N):
y[0]=y0
for i in range (N):
J=f(t0+i*h,y[i])
y[i+1] = y[i] + h*J
return y
#Метод Эйлера усовершенствованный
def Euler_up(f,t0,y0,h,N):
z[0]=y0
for i in range (N):
J=z[i]+f(t0+i*h,z[i])*(h/2)
z[i+1] = z[i] + h*(f(t0+i*h+h/2,J))
return z
#Метод Эйлера-Коши
def Euler_Couchy(f,t0,y0,h,N):
u[0]=y0
for i in range (N):
J=f(t0+i*h,u[i])
O=u[i]+J*h
u[i+1] = u[i] + h*(J+f(t0+(i+1)*h,O))/2
return u
# Метод Рунге_Кутты
def Runge_Kutti(f,t0,y0,h,N):
v[0]=y0
for i in range (N):
K1=f(t0+i*h,v[i])
K2=f(t0+i*h+h/2,v[i]+h*K1/2)
K3=f(t0+i*h+h/2,v[i]+h*K2/2)
K4=f(t0+i*h+h,v[i]+h*K3)
v[i+1] = v[i]+h/6*(K1+2*K2+2*K3+K4)
return v
# Поиск эпсилон
def Epsilon(o,q,x):
S=0
for i in range(x):
if abs(o[i] - q[i]) > S:
S = abs(o[i]-q[i])
return S
t0=0
y0=0.1
T=2
N=16
h=(T-t0)/N
print('h = ',h)
y=[0]*(N+1)
Euler(f,t0,y0,h,N)
z=[0]*(N+1)
Euler_up(f,t0,y0,h,N)
u=[0]*(N+1)
Euler_Couchy(f,t0,y0,h,N)
plt.grid(True)
x=np.linspace(t0,T,N+1)
p=[0]*(N+1)
for i in range(len(x)):
p[i]=Yt(x[i])
Runge_Kutti(f,t0,y0,h,N)
x=np.linspace(t0,T,N+1)
p=[0]*(N+1)
for i in range(len(x)):
p[i]=Yt(x[i])
plt.grid(True)
xx=np.linspace(t0,T,100)
yy=np.linspace(0,0,100)
for i in range(100):
yy[i]=Yt(xx[i])
plt.plot(xx,yy,color='blue',label='Точное решение')
plt.plot(x,y,color='red',label='Явный метод Эйлера',ls='',marker='.', markersize=6)
plt.plot(x,z,color='black',label='Метод Эйлера усовершенствованный',ls='',marker='.', markersize=6)
plt.plot(x,u,color='green',label='Метод Эйлера-Коши',ls='',marker='.', markersize=6)
plt.plot(x,v,color='yellow',label='Метод Рунге-Кутты',ls='',marker='.', markersize=6)
plt.legend()
print('Явный метод = ',Epsilon(p,y,len(x)))
print('Метод Эйлера усовершенствованный = ',Epsilon(p,z,len(x)))
print('Метод Эйлера-Коши = ',Epsilon(p,u,len(x)))
print('Метод Рунге-Кутты = ',Epsilon(p,v,len(x)))
print('y=',y)
print('z=',z)
print('u=',u)
print('v=',v)
