шпорэ

31

6.5.Местные потери

Местные потери энергии вызваны изменениями формы и размера трубопровода, вызывающими деформацию потока. Жидкости, протекая через местные сопротивления, изменяет скорость и образует вихри. После отрыва потока от стенок вихри образуют области, в которых частицы жидкости движутся в основном по замкнутым траекториям.

Каждое местное сопротивление характеризуется значением коэффициента сопротивления ζ, которое приближенно можно считать постоянным для данной формы местного сопротивления.

6.6. Потери энергии на трение по длине

Эти потери возникают в прямых трубах постоянного сечения и при равномерной скорости течения, возрастают пропорционально длине трубы .

Потери энергии на трение по длине связаны с внутренним трением в жидкости, эти потери можно определять по формуле для гидравлических потерь, т. е. h тр = ζ тр v2/(2g).

Поскольку длины труб разные, коэффициент потерь на трение ζтр связывают с относительной длиной трубы l/d: ζ тр = λ* l/d .

Формула для определения потерь на трение по длине называется формулой

Вейсбаха – Дарси. hтр l V 2 d 2g

Коэффициент λ, входящий в формулы для определения потерь по длине называется "коэффициентом потерь на трение по длине", или "коэффициентом Дарси".

33

7. Истечение жидкости через отверстия и насадки при постоянном напоре.

Перелив жидкости из бака в бак производится через отверстия между баками, которые закрываются запорными элементами.

Насадки применяются в моечных устройствах и двигателях, где с их помощью производится распыление жидкости

8.1. Истечение через отверстия при постоянном напоре .

Истечение из резервуара при постоянном напоре и под давлением Р1 над свободной поверхностью через круглое отверстие с острой кромкой.

Через отверстие струя жидкости вытекает в воздушное пространство с атмосферным давлением Р2 =Рат.

Глубина расположения отверстия в дне или на стенке резервуара во много раз больше диаметра отверстия Н0 >> dо (рис.8.1).

К отверстию жидкость подтекает со всех сторон, поэтому в плоскости отверстия частицы движутся по криволинейным траекториям, поэтому за отверстием площадь сечения струи оказывается меньше площади отверстия, происходит сжатие струи. В дальнейшем струя сохраняет свою форму на некотором расстоянии от отверстия.

34 1. Сжатие струи называется совершенным, если стенки резервуара удалены от

центра отверстия на расстояние l > 3d и не оказывают влияния на сжатие струи. В этом случае сечение струи получается наименьшим.

2.Сжатие струи называется несовершенным при l < 3d. в этом случае влияние стенок резервуара на сжатие струи значительно меньше и сечение струи оказывается больше, чем при совершенном сжатии.

8.2. Истечение при совершенном сжатии. Скорость истечения реальной жидкости.

Сжатие струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия ε = Sc/S0 = (dc/d0)2.

Коэффициент сжатия зависит от 1)формы отверстия; 2)положения отверстия относительно стенок резервуара, например, в центре симметрии дна или смещенное от

Для определения скорости в сжатом сечении запишем уравнение Бернулли для живого сечения, соответствующего свободной поверхности жидкости в резервуаре "1-1" и сжатого сечения струи «2 –2», плоскость сравнения выберем по сечению "2-2".

Определим напоры, входящие в уравнение Бернулли.

1.Рассматривается установившееся движение, уровень жидкости не меняется, истечение под постоянным напором: следовательно: геометрический напор z1=H.

2.Давление Р1 на поверхности "1-1" может быть равно атмосферному, больше или меньше атмосферного, поэтому пьезометрический напор равен Р1/ρg.

3.Поскольку уровень жидкости в сечении "1-1" не меняется, скорость V1=0 равна 0.

4.По сечению "2-2" выбрана плоскость сравнения, поэтому геометрический напор равен z2=0.

5.Истечение происходит в атмосферу, поэтому избыточное давление в сечении 2-2" Р2 = Ратм = Рс = 0, пьезометрический напор равен Р2/ρg = 0.

6.Скорость в сжатом сечении V2 = Vc.

7.При ламинарном режиме движения эпюра скоростей близка к параболической, коэффициент Кариолиса принимается равным двум αл ≈2, при турбулентном режиме

35 движении эпюра близка к трапециидальной αт ≈ 1-1,1 приниманется в расчетах равным

где ζ — коэффициент сопротивления отверстия, α - коэффициент Кориолиса, Н = Н1 + Р1 / ρg - напор истечения, сумма геометрического и пьезометрического

Умножив площадь сечения сжатой струи Sc = εSо на скорость струи в сжатом

сечении Vс 2gH , получим выражение для расхода жидкости через отверстие с острой

кромкой при совершенном сжатии Qс ScVс So 2gH

Коэффициентом расхода при истечении из отверстия μ называется произведение коэффициента сжатия ε на коэффициент скорости φ: μ = ε * φ.

На рис. 8.4 показаны составленные А.Д. Альтшулем зависимости для коэффициентов ε, φ и μ для круглого отверстия в функции числа Rе.

36

Безразмерный коэффициент потерь ζ - дзета называется коэффициентом сопротивления и равен отношению величины потерянного напора к скоростному напору.

37

8.4. Истечение при несовершенном сжатии

Сжатие струи называется несовершенным, когда на формирование струи оказывает влияние близость боковых стенок резервуара, то есть расстояние от оси отверстия до стенки l < 3d. Сечение резервуара соизмеримо с сечением отверстия.

Боковые стенки успевают сформировать поток жидкости при подходе к отверстию, и струя сжимается в меньшей степени, чем при истечении из резервуара неограниченных размеров при совершенном сжатии. Увеличивается коэффициент сжатия и

коэффициент расхода.

1. При несовершенном сжатии и больших числах Re коэффициент сжатия ε1 определяется по формуле ε1 = 0,62 +0,38/(S0/S1)

где S0/S1 отношение площади отверстия S0 к площади S1 поперечного сечения резервуара.

2.Коэффициент скорости при несовершенном сжатии φ находят по графику Альтшуля на рис.8.3 по числу Re.

3.Коэффициент сопротивления отверстия ζ можно найти из формулы, связывающей

За плоскость сравнения возьмем сечение 2. Исходные данные по сечению "1-1": z1=h, P/ρg, V1. Исходные данные по сечению "2-2": z2=0, P2=Pатм =0, V1=Vс-скорость в сжатом сечении, S2 = Sc = ε1S0. Напор истечения равен : H (z1 P1 / g) (z2 P2 / g)

HV22 (1 12n2 ).

2g

4.Cкорость в сжатом сечении при несовершенном сжатии струи

8.5. Истечение под уровень

Истечением жидкости в пространство, заполненное этой же жидкостью, называется истечением под уровень. Кинетическая энергия струи теряется на вихреобразование.

Определим скорость и расход, используя уравнение Бернулли для поверхности "1- 1" и сечения "2 – 2", за плоскость сравнения принято – сечение "1-1".

Исходные данные: z1=h1, P1 > Ратм, V1 = 0 , в сечении "2-2" : z2=0, Р2в< Ратм, P2 =- Р2в+ρgh2, скорость в сжатом сечении V2 →?, ξ ≈0,06 – коэффициент

сопротивления отверстия принимают таким же, как при истечении в атмосферу, коффициента Кориолиса α.

39 где Н –напор истечения: разность гидростатических напоров по обе стороны

стенки. Скорость и расход не зависят от высоты расположения отверстия.

где Sc – площадь сжатого сечения струи, S0 – площадь отверстия. Скорость и расход в этом случае определяются, как при истечении в атмосферу.

Значения коэффициентов истечения для затопленного отверстия можно принимать такими же, как при истечении свободной струи в атмосферу.

8.5. Истечение через насадки при постоянном напоре.

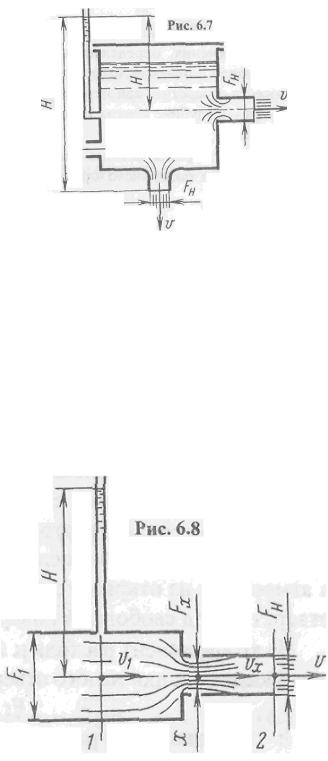
Внешним цилиндрическим насадком называется короткая трубка длиной, равной l = (1÷5)d с острой входной кромкой (рис.8.7). Истечение через такой насадок в атмосферу может происходить в двух режимах.

а) Безотрывной режим течения называется режим истечения, при котором струя после входа в насадок сначала сжимается, потом затем сжатая часть струи расширяется до размеров выходного диаметра и выходит сечением равным сечению насадка.

При истечении жидкости из больших резервуаров через насадки скорость истечения на выходе из насадка и расход определяются по формулам.

Q FН 2gH ,V 2gH ,

40

Для коноидального (плавно сужающегося насадка без сжатия струи на выходе) ε = 1 можно принимать в квадратичной зоне сопротивления μ = φ = 0,97. Коэффициенты истечения могут быть приближенно определены путем

суммирования потерь на отдельных участках потока.

Так, например, для внешнего цилиндрического насадка (рис. 6.8) потерю напора можно представить в виде суммы:

где hп(1+x) потеря при входе в насадок на участке до сжатого сечения струи (х)',hп(х+2) - потеря при расширении потока на участке между сжатым и выходным сечениями.

Предполагая турбулентный режим течения, и выражая эти потери по формулам

получим