Учебно-Технологический_Практикум_УТС.Б_3

Функция SURFL

Функция SURFL строит поверхность Z(X,Y) аналогично функции SURF. Дополнительно имитируется освещение поверхности точечным источником света. Подсветка учитывает рассеивание, отражение и зеркальный эффект.

ФОРМАТЫ ВЫЗОВА:

1. surfl(X,Y,Z) где X,Y – матрицы узлов координатной сетки, Z

– матрица значений функции Z(X,Y) в точках узлов – строит

освещенную поверхность Z(X,Y); Цвет ячеек сетки поверхности не зависит от значения Z, а определяется цветовой палитрой, и положением источника света по умолчанию.

2. surfl(X,Y,Z,P) – дополнительно определяется положение источника света вектором P = [Px,Py,Pz].

Замечание: управление цветовой палитрой будет рассмотрено ниже в пункте:

«Вспомогательные функции и команды 3D графики»

ПРИМЕР.

Построить поверхность функции: Z=exp(-X.^2-Y.^2).*sin(-X.^2-Y.^2) , -2<=X,Y<=2.

Решение.

x=[-2:0.1:2]; y =[-2:0.1:2]; [X,Y]=meshgrid(x,y); Z=exp(-X.^2-Y.^2).*sin(-X.^2-Y.^2); surfl(X,Y,Z,[1,3,1]);

Рис. 1.1.16. График поверхности, построенный функцией SURFL

21

Вспомогательные функции и команды 3D графики

Функция COLORMAP

Для всех 3D функций, поддерживающих функциональную окраску поверхности актуально понятие цветовой палитры, или - цветовой карты – colormap, в терминах MATLAB. Цветовая карта – это матрица M, состоящая из трех столбцов и произвольного числа строк. Каждая строка определяет интенсивность красного, зеленого и синего цветов в диапазоне [0 1]. Иными словами – каждая строка определяет конкретный цвет палитры. Например, строка [1 0 0] – определяет чисто красный цвет, строка [0.5 0 0] - оттенок красного цвета, [0 0 0] - черный цвет, [0.1 0.1 0.1] – оттенок серого цвета.

ФОРМАТ ВЫЗОВА:

1.colormap(M), где M – матрица цветовой карты размера

[N x 3]. В MATLAB есть предустановленные цветовые карты

функциональной окраски – hsv, hot, copper, gray, pink, cool, summer, winter, bone и другие.

ПРИМЕР.

Построить освещенную поверхность функции: Z=-exp(-X.^2-Y.^2).*sin(-X.^2-Y.^2) , -2<=X,Y<=2.

Окрасить поверхность оттенками серого цвета. Решение.

x=[-2:0.1:2]; [X,Y]=meshgrid(x);

Z=-exp(-X.^2-Y.^2).*sin(-X.^2-Y.^2); C1=[0:0.001:1]'; C2=С1;C3=C2; M=[C1 C2 C3]; colormap(M); surfl(X,Y,Z,[3,4,10]);

0.4

0.3

0.2

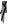
0.1 0

-0.1 2

Рис. 1.1.17. График поверхности, построенный функцией SURFL. Палитра – оттенки серого цвета.

22

Команда SHADIND

SHADING – команда управления типом затенения 3D поверхности. Опции команды:

-faceted – опция по умолчанию. Затенение выполняется цветами активной палитры отдельных ячеек сетки поверхности в зависимости от положения источника света. Линии сетки видны;

-flat – аналогично faceted, но линии сетки убираются;

-interp – аналогично flat, но между отдельными ячейками сетки выполняется градиентное сглаживание цвета.

ПРИМЕР.

Построить освещенную поверхность функции: Z=-X.*exp(-X.^2-Y.^2), -2<=X,Y<=2.

Окрасить поверхность оттенками серого цвета. Решение.

x=[-2:0.1:2]; [X,Y]=meshgrid(x); Z=-X.*exp(-X.^2-Y.^2);

colormap(gray); surfl(X,Y,Z,[-2,-2, 2]); shading interp;

Рис. 1.1.18. График поверхности, построенный функцией SURFL. Палитра – предустановленная - gray - оттенки серого цвета. Затенение

– интерполяционное.

23

1.2 СКРИПТЫ MATLAB

MATLAB может выполнять не только отдельные команды в интерактивном режиме. Системой предоставляется возможность записать последовательность команд в текстовый файл, а затем выполнить всю эту последовательность. Текстовый m-файл, содержащий последовательность команд MATLAB, называется скриптом. После сохранения скрипт становится допустимой командой MATLAB, причем имя команды – это имя соответствующего m-файла без расширения.

Скрипты MATLAB, это средство автоматизации выполнения отдельных команд и фактически являются аналогами процедур классических языков программирования. Следовательно, MATLAB – это не только математический программный пакет, но и язык программирования. Запустить скрипт можно прямо - в командном окне MATLAB, или косвенно – в другом скрипте. Обязательное условие – файл скрипта должен размещаться в каталоге, который входит в список катало-

гов MATLAB.

Технически скрипт MATLAB можно написать, используя любой текстовый редактор, но MATLAB предоставляет для этого возможности встроенного редактора-отладчика.

Для создания нового скрипта необходимо выбрать в меню File путь

New – Script - Рис 1.2.1.

Рис. 1.2.1 Создание нового скрипта MATLAB

При этом активируется редактор – отладчик MATLAB, в котором можно набрать текст скрипта, сохранить скрипт в выбранном каталоге, выполнить отладку, запустить скрипт на выполнение. По умолчанию, новый скрипт имеет имя Untitled – безымянный. Рекомендуется скриптам MATLAB сразу давать имена, соответствующие содержанию скрипта.

24

ПРИМЕР.

Написать скрипт, построения освещенной поверхности функции:

Z= sin(-X.^2-Y.^2).*exp(-X.^2-Y.^2), -1.5<=X,Y,<=1.5.

Поместить источник света в точку Р(-2,-1, 1). Тип затенения - flat. Цветовая карта – встроенная - gray.

Оформить график. Решение.

Создаем новый скрипт, сохраняем его с именем Demo3D, записываем

вфайл скрипта:

-справочный комментарий, который будет выводиться в командное окно MATLAB по команде help Demo3D;

- команды скрипта.

Если текст скрипта не содержит ошибок, запустить скрипт на выполнение можно из окна редактора-отладчика, нажав на кнопку запуска, на инструментальной панели, или выбрав пункт Run в меню Debug, или нажав функциональную клавишу F5 на клавиатуре.

Окно редактора-отладчика с текстом скрипта Demo3D показано на Рис. 1.2.2., график поверхности – на Рис. 1.2.3.

Рис. 1.2.2 Окно редактора MATLAB с текстом файла скрипта Demo3D.m

25

0.1

0

-0.1

Z

-0.2

-0.3

-0.4 2

Рис. 1.2.3 Поверхность – результат работы скрипта Demo3D

2. ПРАКТИЧЕСКАЯ ЧАСТЬ

ЗАДАНИЕ 1

Для заданного преподавателем варианта из Таблицы 2.1, найти выражение разложения в ряд Тейлора T(x) по целым неотрицательным

26

Представление функции F(x) в виде степенного ряда (1), называется разложением функции F(x) в ряд Тейлора или рядом Тейлора. Представление функции F(x) в виде степенного ряда (2), называется разложением функции F(x) в ряд Маклорена. Иногда, формы (1) и (2) объединяют, и соответствующие разложения называют рядом ТейлораМаклорена. На практике, члены ряда степени выше n, отбрасывают и равенства (1) и (2) становятся приближенными. Ошибка приближения

27

ПРИМЕР. Дано:

F(x)=sin(x), 0<=x<=1.

Требуется:

Найти разложение в ряд Тейлора пятой степени функции F(x) в

Решение.

Функция F(x) приближается рядом Тейлора в окрестности точки, отличной от нуля. Следовательно, формула для ряда будет иметь вид

(1), при х0=0.5:

Откроем редактор MATLAB, сохраним файл скрипта как Teylor.m Текст скрипта:

%Приближение функции F(x)=sin(x) рядом Тейлора %пятой степени на отрезке [0,1] в окрестности точки x0=0.5 %Печатаются графики:

%1- функции и ее приближения %2-ошибки приближения x=0:0.05:1;

x0=0.5;

a=[sin(x0)/factorial(0), cos(x0)/factorial(1),-sin(x0)/factorial(2), -cos(x0)/factorial(3),sin(x0)/factorial(4), cos(x0)/factorial(5)]; T=a(1)+a(2)*(x-x0)+a(3)*(x-x0).^2+a(4)*(x-x0).^3+ +a(5)*(x-x0).^4+a(6)*(x-x0).^5;

plot(x,sin(x),'-db',x,T,'-rs')

title('Приближение рядом Тейлора пятой степени функции F=sin(x)'); legend('Функция sin(x)','Ряд Тейлора');

xlabel('X'); ylabel('Y');grid on ; figure plot(x,abs(sin(x)-T),'-bh');

title('Ошибка приближения eps=abs(sin(x)-T(x)'); legend('Ошибка приближения');

xlabel('X'); ylabel('Y'); grid on;

Полученные графики показаны на Рис. 2.1.1

28

ЗАДАНИЕ 3

Для заданного варианта палитры из Таблицы 2.3, написать скрипты для построения освещенной поверхности функции peaks, при всех ти-

3. КОНТРОЛЬНЫЕ ВОПРОСЫ

2D ГРАФИКА MATLAB. ФУНКЦИЯ PLOT

2D графика MATLAB. Функция POLAR

Функции MATLAB для оформления графиков

Меню и инструменты графического окна MATLAB

3D графика MATLAB. Функция PLOT3

3D графика MATLAB. Функция MESH

3D графика MATLAB. Функция MESHC

3D графика MATLAB. Функция CONTOUR3

3D графика MATLAB. Функция SURF

3D графика MATLAB. Функция SURFL

Вспомогательные функции 3D графики. Функция MESHGRID

Вспомогательные функции 3D графики. Функция COLORMAP

Вспомогательные команды 3D графики. Команда SHADING

Скрипты MATLAB. Основные характеристики.

Скрипты MATLAB. Работа в редакторе MATLAB

30