2.13. Построение равных многоугольников

Многоугольник, равный заданному, можно построить по координатам точек вершин и методом триангуляции.

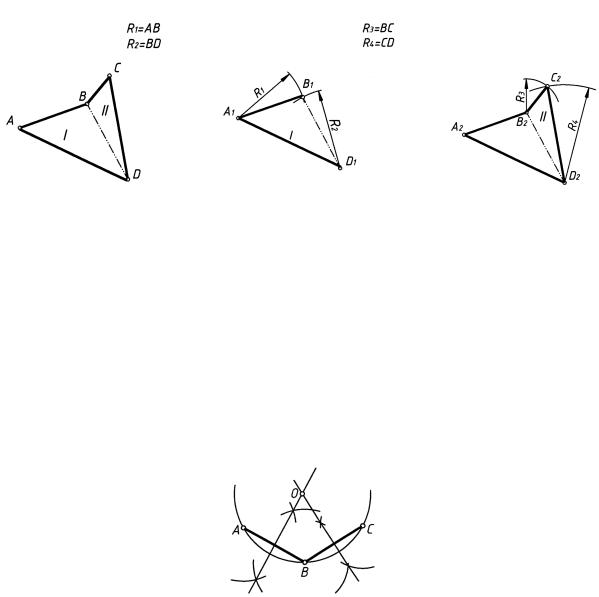
Метод триангуляции. Этот метод основан на разбивке данного многоугольника на треугольники и последовательном построении треугольников по данным сторонам, например:

а) разбиваем данный многоугольник ABCD на два треугольника ABD и BCD (рис. 18);

б) приняв за основание сторону AD, проводим отрезок A1D1 = AD и строим треугольник A1B1D1, равный треугольнику ABD (см. рис. 17) по трем данным сторонам (рис. 19);

в) приняв за основание сторону B1D1, строим треугольник B2C2D2, равный треугольнику BCD (рис. 20).

3. ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ И ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ

3.1. Определение центра дуги

Взять на дуге окружности (рис. 21) три произвольно расположенные точки A, В и С. Отрезки AB и BC — хорды заданной дуги. Точка пересечения перпендикуляров, проведенных через середины хорд, определяет положение центра O исходной дуги. Построение основано на определении окружности как геометрического множества точек, удаленных от центра на заданное расстояние R.

Рис. 21

9

3.2.Определение центра окружности

Взаданной окружности (рис. 22) провести две не параллельные между собой хорды AB и CD. Через середины хорд провести перпендикуляры, пересечение которых определяет положение центра O исходной окружности.

Рис. 22

3.3.Деление окружности на три, шесть и двенадцать частей

Вокружности заданного радиуса R (рис. 23) провести через центр O взаимно перпендикулярные диаметры AB и CD. Из любой точки конца диаметра (например, из точки А) провести дугу радиуса R = АО до пересечения с окружностью в точках 1 и 2. Отрезок 12 — искомая сторона правильного вписанного треугольника 1В2.

Рис. 23

Отрезки A1 = A2 и C1 = D2 соответственно равны сторонам правильных вписанных шестиугольника и двеннадцатиугольника. Для построения недостающих вершин многоугольников достаточно провести из противоположного конца диаметра окружности (в нашем случае — из точки B) дугу того же радиуса R до пересечения с окружностью.

3.4. Деление окружности на четыре и восемь частей

Провести два взаимно перпендикулярных диаметра AB и CD (рис. 24). Отрезки AC = CB = BD = DA, соединяющие концы диаметров, являются сторонами правильного вписанного четырехугольника.

10

Рис. 24

Для деления окружности на восемь частей необходимо построить перпендикуляры к серединам сторон четырехугольника и продолжить их до пересечения с окружностью. Отрезок AM — сторона правильного восьмиугольника, вписанного в окружность.

3.5. Деление окружности на пять и десять частей

Провести два взаимно перпендикулярных диаметра AB и CD (рис. 25) и разделить радиус OB пополам в точке M. Из точки M, как из центра, провести дугу радиуса MC до пересечения ее с диаметром AB в точке K. Отрезок CK равен стороне правильного вписанного пятиугольника, отрезок OK равен стороне правильного вписанного десятиугольника.

Рис. 25

3.6. Деление окружности на семь частей

Из точек A и B концов горизонтального диаметра AB (рис. 26) провести дуги радиуса R = AO = BO и отметить точки их пересечения 1 и 2 с исходной окружностью.

Рис. 26

11

На пересечении хорды 12 с радиусом OD отметить точку M. Отрезок OM равен стороне правильного вписанного семиугольника. Для его построения измерителем последовательно отложить соответствующие отрезки на исходной окружности.

3.7. Деление окружности на n равных частей

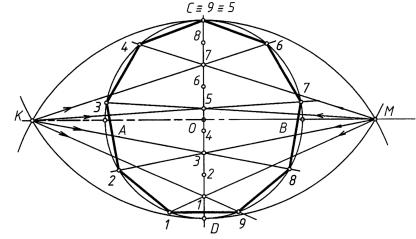
Провести в окружности заданного радиуса R два взаимно перпендикулярных диаметра AB и СD (рис. 27) и разделить один из диаметров, например CD, на заданное число равных частей (n = 9). Из точек C и D, как из центров, провести дуги окружностей радиуса 2R до их пересечения с диаметром AB в точках K и M.

Рис. 27

Используя полученные точки K и M в качестве центров, провести семейство лучей через четные или нечетные (как в нашем случае) точки деления диаметра CD до пересечения с заданной окружностью. Полученные на окружности точки 1, 2, . . . , 9 — искомые точки деления окружности на заданное число частей. Описанный способ приближенный; дуги, на которые разделена окружность, в действительности не равны одна другой. Однако погрешность не превышает 0,01R, что для практических целей можно считать достаточным.

3.8. Построение правильных многоугольников по заданной стороне

Сторону AB (рис. 28) разделить точкой O пополам и восстановить в этой точке перпендикуляр к отрезку AB. Из точек A и B провести дуги радиуса R = AB до пересечения их в точке 1. Треугольник A1B — искомый равносторонний треугольник.

Для построения квадрата надо восстановить в точках A и B перпендикуляры к отрезку AB и продолжить их до пересечения в точках C и D с дугами радиуса R = AB. Квадрат ACDB искомый.

В квадрате ACDB провести диагонали и отметить точку 2 их пересечения. Разделить расстояние между точками 1 и 2 пополам точкой 3, которая будет служить центром окружности для вписанного в нее правильного пятиугольника со стороной AB.

Последовательно откладывая расстояние 13 от точки 1 вверх по перпендикуляру, отметить точки 4, 5, 6, . . . , n, которые будут служить центрами окружностей для

12