condesir_sost
.pdf
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ МГУ
Физика
конденсированного
состояния
Курс лекций
Михаил Исаакович Трибельский
Москва 2013 г.
11.02.2013 № 1
Основная литература: Ч. Киттель Введение в физику твердого тела
Физика конденсированного состояния – наука о структуре и свойствах конденсированных веществ.
Конденсированные вещества – сильное межатомное взаимодействие. Расстояние между соседними атомами порядка 10-8 см.
Деление по категориям
Физика конденсированного состояния = физика твердого тела + физика жидкостей + физика полимеров.
Физика твердого тела = физика кристаллов (упорядоченные структуры) + физика аморфных в-в (неупорядоченные структуры).
Физика кристаллов = физика нормальных кристаллов + физика квантовых кристаллов.
Физика нормальных кристаллов = физика металлов + физика полупроводников + физика диэлектриков.
Физика металлов = физика нормальных металлов + физика сверхпроводящих металлов.
1
Физика сверхпроводящих металлов = физика сверхпроводников первого рода + физика сверхпроводников второго рода + физика смешанного состояния
……………………………………………………………………………
Физика жидкостей = физика ньютоновых жидкостей + физика жидких кристаллов + физика реологических жидкостей .
Физика ньютоновых жидкостей = физика нормальных жидкостей + физика сверхтекучих жидкостей
Физика сверхтекучих жидкостей = физика сверхтекучих бозонов (He4) + физика сверхтекучих фермионов (He3).
………………………………………………………………
Физика жидких кристаллов = физика нематиков + физика смектиков + физика холестериков.
Физика реологических жидкостей = …
Физика полимеров = …
Деление по масштабам
Физика макрообъектов L > 100 нм (свойства не зависят от размеров) 
Физика мезообъектов 0.1 нм << L << 100 нм (свойства зависят от размера)
Физика макрообъектов = физика монокристаллов + физика поликристаллов.
Физика мезообъектов = классическая + квантовая
……………………………………………………………..
2
Деление по размерности
3D объекты + 2D объекты (тонкие пленки) + 1D объекты (нити, волокна, трубки) + 0D объекты (квантовые точки).
…………………………………………………………………………………
Деление по структуре
Идеальные структуры.
Структуры с дефектами (дислокации) и/или с примесями. 
Сплавы и композиты.
…………………………………………………………………………………..
Свойства монокристаллов
Структура идеального кристалла. Описание
Идеальный кристалл = бесконечное повторение в пространстве одной и той же структурной единицы (элементарной ячейки).
3
Т – вектор трансляции; a и b – основные векторы трансляций.
Что такое базис? Это некоторая идентичная группа атомов (или один атом), связанная с каждой точкой решетки.
4
ВАЖНО: Для данной кристаллической структуры всегда можно выбрать несколько кристаллических решеток, а для каждой решетки – несколько кристаллографических систем координат. Мы не можем выбрать базис, пока не выбраны решетка и система координат, которой мы хотим пользоваться. Однако результат (например, рентгенограмма кристалла) оказывается независящим от того, какой конкретно выбор сделан.
Примитивная ячейка – элементарная ячейка наименьшего размера.
Векторы примитивных трансляций – векторы основных трансляций примитивной ячейки. Их часто выбирают в качестве ортов
кристаллографических осей.
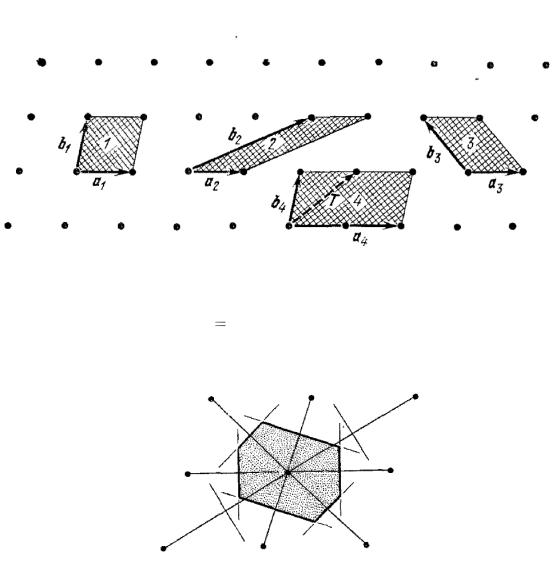
Ячейки 1, 2, 3 – примитивные; |
4 – нет (1, 2, 3 имеют одинаковый объем). |
Объем примитивной ячейки V |
| (a[bc]) | . |
Другой выбор примитивной ячейки (ячейка Вигнера-Зейтца).
5
ЗАДАЧА 1: Доказать, что для данной кристаллической решетки объем ромбической примитивной ячейки = объему ячейки Вигнера-Зейтца1.
ЗАДАЧА 2: Доказать, что для данной кристаллической решетки объемы всех возможных примитивных ячеек одинаковы2.
ЗАДАЧА 3: Доказать, что для данной кристаллической решетки при любом из возможных выборов примитивной ячейки число атомов в базисе остается неизменным3.
Преобразования симметрии. Решетка обладает определенной симметрией, если при применении преобразований этой группы симметрии она переходит сама в себя.
Трансляционная симметрия – обязательная.
Обычно + к ней несколько точечных преобразований симметрии:
Вращение на определенный угол вокруг оси, проходящей через узел решетки (вращательная симметрия) ;
Отражение относительно плоскости, проходящей через узлы решетки (зеркальная симметрия); 
Применение и того и другого преобразования последовательно.
Группа вращательной симметрии характеризуется целым числом n, показывающим сколько раз решетка перейдет сама в себя при повороте вокруг оси симметрии на угол 2 . Например, для квадратной ячейки n=4.
Наличие зеркальной симметрии обозначают буквой m. Число этих показывает, сколько плоскостей симметрии имеет данная ячейка. Например, mm – означает две плоскости.
Благодаря наличию симметрии все возможные решетки можно проклассифицировать в соответствии с группой симметрии данной решетки Число таких групп конечно. Например, в двумерном сл. существует только 5 типов решеток:
6
Не бывает двумерных кристаллов с осями симметрии 5, 7 и более высокого порядка (почему?).
Но бывают кристаллов с осями приближенной вращательной симметрии любого порядка (квазикристаллы или шехтманиты) – Дан Шехтман (Нобелевская премия по химии 2011 г.).
В 3D существует 32 группы симметрии кристаллических решеток (Иоганн Гессель, 1830 г., Огюст Браве, 1849 г.). Браве все сделал на 19 (!) лет позже и
7
при своей классификации пропусти одну группу – он нашел только 31, в то время, как Гессель нашел все 32. Однако, в литературу кристаллические решетки вошли, как решетки Браве.
8
18.02.2013 № 2
Положение и ориентация плоскостей в кристалле
9