
Построение функции спроса

Метод наименьших квадратов
-
Линейная аппроксимация
Линейная модель представлена в виде:
 ,
где
,
где
 - погрешность. Суть метода состоит в
том, чтобы минимизировать сумму квадратов
погрешностей для данной модели:
- погрешность. Суть метода состоит в
том, чтобы минимизировать сумму квадратов
погрешностей для данной модели:

Составим таблицу исходных данных – пар чисел (p, D(p)) также в порядке возрастания значений параметра p.
Таблица 2
Оценивание функции спроса методом наименьших квадратов.
|
i |
pi |
Ni |
pi * Ni |
D(pi) |
D(pi) *Ni |
Pi2 * Ni |
D(pi) * pi * Ni |
D*(pi) |
Ni * [D(pi) – D*(pi)] |
Ni * [D(pi)-D*(pi)]2 |
|
1 |
8000 |
4 |
32000 |
50 |
200 |
256000000 |
1600000 |
52,75 |
-11,00 |
30,26 |
|
2 |
9000 |
5 |
45000 |
46 |
230 |
405000000 |
2070000 |
45,93 |
0,35 |
0,02 |
|
3 |
10000 |
8 |
80000 |
41 |
328 |
800000000 |
3280000 |
39,11 |
15,14 |
28,64 |
|
4 |
11000 |
4 |
44000 |
33 |
132 |
484000000 |
1452000 |
32,29 |
2,85 |
2,04 |
|
5 |
11500 |
2 |
23000 |
29 |
58 |
264500000 |
667000 |
28,88 |
0,25 |
0,03 |
|
6 |
12000 |
6 |
72000 |
27 |
162 |
864000000 |
1944000 |
25,47 |
9,21 |
14,13 |
|
7 |
12500 |
4 |
50000 |
21 |
84 |
625000000 |
1050000 |
22,05 |
-4,22 |
4,45 |
|
8 |
13000 |
6 |
78000 |
17 |
102 |
1014000000 |
1326000 |
18,64 |
-9,86 |
16,22 |
|
9 |
13500 |
1 |
13500 |
11 |
11 |
182250000 |
148500 |
15,23 |
-4,23 |
17,92 |
|
10 |
14000 |
2 |
28000 |
10 |
20 |
392000000 |
280000 |
11,82 |
-3,65 |
6,64 |
|
11 |
14500 |
2 |
29000 |
8 |
16 |
420500000 |
232000 |
8,41 |
-0,82 |
0,34 |
|
12 |
15000 |
6 |
90000 |
6 |
36 |
1350000000 |
540000 |
5,00 |
5,99 |
5,98 |
|
|
- |
50 |
584500 |
- |
1379 |
7057250000 |
14589500 |
- |
0,00 |
126,68 |
|
|
|
|
11690 |
- |
27,58 |
141145000 |
291790 |
- |
- |
- |



k
– число групп, k
= 12;
 50
50
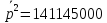

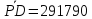

Оценка параметров а*, b* произведена по формуле с учетом посчитанных значений:


После подстановки:


Таким образом, теоретическая функция спроса имеет вид:
D*(p) = - 0,0068*p +107,32
Рассчитаны восстановленные значения спроса при наших значениях цены: D*(p)
Произведена проверка правильности решения по следующему критерию:
 =
0 – все расчеты верны.
=
0 – все расчеты верны.
Также рассчитана остаточная сумма квадратов:
SS1= = 126,88
= 126,88
Расчет оптимальной цены для линейной зависимости
Теперь перейдем к расчету оптимальной цены при различных уровнях издержек p0. Для этого мы должны максимизировать прибыль:
(p - p0.) D*(p) = (p. – p0.)(a*p + b*).
Продифференцируем это выражение по p и приравняем 0 производную, а также учтем, что a* = -0,0068,b* = 107,32
2a*pопт. – а*р0 +b* = 0,

Сравним (табл.4) оптимальные цены, найденные с помощью метода наименьших квадратов (pопт.2) и рассчитанные ранее с помощью первого метода (pопт.1). Таблица 4
|
|
pопт.1 |
pопт.2 |
|
4000 |
10000 |
9891 |
|
6400 |
11000 |
11091 |
|
8500 |
12000 |
12141 |
|
11000 |
12500 |
13391 |
|
12000 |
14000 |
13891 |
Вывод: оптимальные цены незначительно отличаются как в большую, так и в меньшую сторону от тех, которые мы нашли в начале.
-
Степенная аппроксимация
Оценка параметров степенной аппроксимации проводится аналогичным образом с той лишь разницей, что для нее мы используем величину, называемую логарифмом спроса.
Рассмотрим следующую модель:
 -
не является линейной по параметрам.
Логарифмируем ее:
-
не является линейной по параметрам.
Логарифмируем ее:
 .
Произведем замену переменных:
.
Произведем замену переменных:

 ;
;
 .
Получили следующее выражение:
.
Получили следующее выражение:
 – модель,
линейная по параметрам.
– модель,
линейная по параметрам.
Результаты расчетов показаны в Таблице 3, где использованы указанные выше параметры (pi ; fi ; Di). На их основе посчитаны средние значения, как средневзвешенные:


Таблица 3.
|
i |
Ni |
ti |
yi |
Ni * ti |
Ni * yi |
Ni * ti2 |
Ni * ti * yi |
|
|
D**(pi) |
(D**(pi)-D(pi))2*Ni |
|
1 |
4 |
8,99 |
3,91 |
35,95 |
15,65 |
323,08 |
140,63 |
4,36 |
-1,77 |
77,92 |
3117,09 |
|
2 |
5 |
9,1 |
3,83 |
45,52 |
19,14 |
414,5 |
174,3 |
3,95 |
-0,63 |
52,16 |
189,77 |
|
3 |
8 |
9,21 |
3,71 |
73,68 |
29,71 |
678,64 |
273,63 |
3,60 |
0,95 |
36,43 |
167,16 |
|
4 |
4 |
9,31 |
3,5 |
37,22 |
13,99 |
346,38 |
130,15 |
3,27 |
0,90 |
26,33 |
178,06 |
|
5 |
2 |
9,35 |
3,37 |
18,7 |
6,73 |
174,85 |
62,97 |
3,12 |
0,50 |
22,63 |
81,21 |
|
6 |
6 |
9,39 |
3,3 |
56,36 |
19,78 |
529,33 |
185,74 |
2,97 |
1,93 |
19,57 |
330,91 |
|
7 |
4 |
9,43 |
3,04 |
37,73 |
12,18 |
355,96 |
114,88 |
2,84 |
0,84 |
17,03 |
62,98 |
|
8 |
6 |
9,47 |
2,83 |
56,84 |
17,0 |
538,39 |
161,03 |
2,70 |
0,79 |
14,90 |
26,42 |
|
9 |
1 |
9,51 |
2,4 |
9,51 |
2,4 |
90,45 |
22,81 |
2,57 |
-0,17 |
13,10 |
4,43 |
|
10 |
2 |
9,55 |
2,30 |
19,09 |
4,61 |
182,28 |
43,96 |
2,45 |
-0,29 |
11,58 |
4,97 |
|
11 |
2 |
9,58 |
2,08 |
19,16 |
4,16 |
183,63 |
39,85 |
2,33 |
-0,50 |
10,27 |
10,32 |
|
12 |
6 |
9,62 |
1,8 |
57,7 |
10,75 |
554,78 |
103,38 |
2,21 |
-2,53 |
9,15 |
59,59 |
|
|
50 |
|
|
467,46 |
156,1 |
4372,27 |
1453,33 |
|
0,00 |
|
4232,92 |
|
|
|
|
|
9,35 |
3,12 |
87,45 |
29,07 |
|
|
|
|
k
– число групп, k
= 12;
 50.
50.
Средние значения:

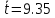

 .12
.12
Оценка параметров а*, b* произведена по формуле с учетом посчитанных значений:


После подстановки:


Восстановленная зависимость:

Рассчитаны
восстановленные значения спроса при
наших значениях цены с помощью операции
потенцирования значения:. .
.

Произведена проверка правильности решения по следующему критерию:
 =
0 – все расчеты верны.
=
0 – все расчеты верны.
Также рассчитана остаточная сумма квадратов:
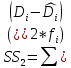 =
4232,9
=
4232,9
Расчет оптимальной цены для восстановленной степенной зависимости
Аналогично линейному случаю, определим оптимальную розничную цену pопт. при различных значениях издержек. А именно, решим задачув случае степенной зависимости:
(p
– p0.)с*pα*→
![]() .
.
Точка, в которой достигается максимум, не меняется при умножении максимизируемой функции на константу. Поэтому переходим к задаче:
(p
– p0.)pα*
= f(p)→
![]() .
.
Для нахождения максимума функции продифференцируем ее и приравняем производную к 0:
![]() .
.
Продифференцируем f(p), используя правило дифференцирования произведения функций:
![]() α*
+ (p
– p0)(α*)pα*
-1
=0.
α*
+ (p
– p0)(α*)pα*
-1
=0.
Итак, необходимо решить линейное уравнение относительно неизвестного p:
p – α*p + p0.α* = 0.
Получим оптимальное значение розничной цены:

Таблица 4
|
|
pопт.1 |
pопт.3 |
|
4000 |
10000 |
5666,7 |
|
6400 |
11000 |
9066,7 |
|
8500 |
12000 |
12042 |
|
11000 |
12500 |
15583 |
|
12000 |
14000 |
17000 |
Общий вывод:На основании того, что SS1<SS2 можно сделать вывод, что предпочтительней работать с линейной моделью для дальнейшей оценки, т.к. она более точно приближает исследуемую функцию спроса.
Библиография
1. Орлова Л.А. Методическая разработка «Функция спроса и метод наименьших квадратов», электронная версия, М.: Лаборатория экономико-математических методов в контроллинге, 2007 (электронный вариант). – 21 с.
2. Орлов А.И. Прикладная статистика. Учебник. - М.: Издательство «Экзамен», 2004. - 656 с.
3. Орлов А.И. «Эконометрика» http://www.orlovs.pp.ru




