16. Расчет электрической цепи при наличии взаимной индуктивности

Для данной электрической цени (рис. 9), содержащей две индуктивно связанные между собой индуктивности ирассчитаем токи и мощности,,во всех ветвях и всей цепи. Проверить баланс активных и реактивных мощностей.

Построить топографическую векторную диаграмму. Индуктивная связь двух элементов цепи характеризуется коэффициентом связи .

Включение индуктивностей исогласное, звёздочками указываем однополярные зажимы обмоток.

Рис.9.

Через коэффициенты связи и величины индуктивностииопределим взаимную индуктивностьМ и её реактивное сопротивление Х_М.

мГН

Ом

Индуктивность взаимно не связана с другими индуктивностями цепи и поэтому токи,определяются также, как в цепи при(см. решение задачи для схемы).

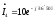
Комплексный ток в неразветвлённом участке цепи будет определяться по 1-му закону Кирхгофа.

Для определения токов ,,введем контурные токиии сделав подстановку

, ,

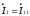оставим 2 уравнения по II закону Кирхгофа:

Далее, сделав соответствующую подстановку и решив совместно систему 2 уравнений, находим контурные токи и,a после этого неизвестные токи ,,и.

Баланс активных мощностей для цепи со взаимной индуктивностью определяется также, как и для цепи при

;

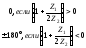
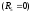
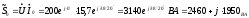
Баланс реактивных мощностей

где

-начальная фаза тока -ветви

-начальная фаза тока -ветви

Для удобства построения векторной диаграммы определим следующие напряжения: (Рис.10)

V. Электрические фильтры

Под электрическим фильтром будем понимать пассивный четырёхполюсник, пропускающий некоторую определённую полосу частот с малым затуханием и подавляющий все остальные частоты.

Полоса частот, для которых затухание мало, называется полосой пропускания или полосой прозрачности. Остальные частоты составляют полосу подавления или полосу непрозрачности.

В настоящей работе рассматриваем так называемые реактивные фильтры, в качестве которых договоримся использовать реактивные, симметричные, согласованные на выходе четырёхполюсники

Т- и П-образные структуры.(Рис. 1,2).

Рис. 1 Рис. 2

Можно показать, что если,

то свойства Т- и П-образных фильтров будут в значительной мере одинаковыми (Рис.З,4).

Рис. 3 Рис. 4

Условие полосы прозрачности фильтра.

Определение.

Под полосой прозрачности реактивного фильтра будем понимать полосу частот, для которых

4

Получим условия полосы прозрачности для фильтров (Рис.З,4). Для симметричного четырёхполюсника известно(см[4]-(81)).

He трудно показать, что для схем Рис.3, 4

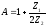
Так как ([4]-(84)), то

(2)

Равенство (2) должно выполняться для любых частот, в том числе и для полосы прозрачности(см(1)).

Таким образом условие полосы прозрачности имеет вид:

(3)

Для реактивных фильтров число вещественное» поэтому для выполнения (3) достаточно чтобы:

или

и наконец

(4)

Знакам равенства соответствуют граничные частоты, которые можно найти решив совокупность уравнений:

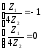
Амплитудо-частотная (АЧХ) и фазо-частотная (ФЧХ) характеристики фильра.

6

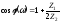
Под АЧХ понимается зависимость затухания от частоты . Под ФЧХ понимается зависимость сдвига по фазе от частоты. Полоса прозрачности:(АЧХ)

(ФЧХ)

Полоса подавления , поэтому. Чтобы левая часть (2) была вещественной, необходимо чтобы, т.е.или. Далее вещественная часть (2) должна быть равна,, т.е.

Так как , то

Как видно из неравенства в полосе подавления величина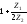либо больше +1, либо меньше -1. Однакоможет быть только больше +1. Отсюда вытекает, что

Если , тои угол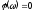

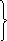
Если , тои угол

В обоих случаях:

Полученное выражение представляет собой амплитудно-частотную характеристику в полосе подавления.

Таким образом АЧХ имеет вид:

а) в полосе прозрачности

б) в полосе подавления:

ФЧХ же будет:

а) в полосе прозрачности

б) в полосе подавления: