12. Символический метод. Основные понятия

Для определения в произвольный момент времени величины переменного токазаданной частоты необходимо знать два числа, например, амплитуду и его начальную фазу. Однако, вместо двух чисел можно пользоваться одним, но комплексным. Комплексным числом или комплексом называется су­мма вещественного числа и мнимого, гденазывается мнимой единицей и обозначается в электротехнике буквой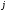. На комплексной плоскости комплексное число изобра­жается

(Рис.20)

где

Поворотный множитель показывает, что вектор повернут относительно вещественной положительной полуоси на уголпро­тив направления движения часовой стрелки.

Отрицательному значению угла соответствует поворот векто­ра по часовой стрелке.

Рис 20.

При расчете цепей символическим методом необходимо учесть

переход от алгебраической формы комплексного числа к показа­тельной и обратно (см. приложение)

Источник напряжения, э.д.с., ток изменяющиеся по синусоида­льному закону могут быть представлены в комплексной форме

Комплексные выражения величин, изменяющихся до гармони­ческому закону, обозначаются прописными печатная буквами с точками над ними ,,, а модули этих значений записываются теми же буквами, но без точек над ними,,.

Сопротивление полное электрическое в комплексной форме обозначается Z, а модуль Z.

в алгебраической форме комплексное значение сопротивления будет равно:

Аналогично запишутся проводимости: ,

Например, для последовательной цепи ,,.

13. РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА СИМВОЛИЧЕСКИМ МЕТОДОМ

Для расчета разветвленной электрической цепи переменного тока символическим методом напряжение цепи и сопротивление каждого участка следует предварительно выразить в символичес­кой формe (рис. 21)

Рис. 21.

Полное сопротивление электрической цепи (Рис.22)

Рис.22

После этого находят ток в неразветвленном участке цепи

и токи в параллельных ветвях ;или

; ;

Правильность полученных значений токов проверяют по I закону Кирхгофа

а напряжение по II закону Кирхгофа

Мощности всей цепи в комплексном виде находятся

где - сопряженный комплекс тока на неразветвленном участкецепи

Активная мощность всей цепи

Реактивная мощность всей цепи

Мощности на участках цепи

Баланс активных и реактивных мощностей

14. Индуктивно связанные электрические цепи

Рассмотрим особенности расчета цепей, в которых есть индуктивные или магнитно связанные катушки. В индуктивно связанных элект­рических цепях поток одной из катушек пронизывает другие и наводит в них э.д.с. взаимоиндукции, которые должны быть учтены при расчете. При согласном включении тока в обоих элементах цепи в любой момент времени имеют одинаковые направления относительно одноименных зажимов в цепи, а потому магнитные потоки самоиндукции и взаимной индукции, сцепленные с каждым элементом, складываются, т.е. взаимная индуктивность по­ложительна. На схеме звездочками следует обозначить одноименные зажимы катушек (начала катушек).

При встречном включении токи в обоих элементах цепи в любой момент времени направлены противоположно относительно одноиме­нных зажимов, поэтому магнитные потоки самоиндукции и взаимо­индукции, сцепленные с каждым элементом, всегда различны по, знаку, т.е. вычитаются.

Взаимная индуктивность будет отрицательной. Индуктивная связь двух элементов цепи может еще характеризоваться коэфи-циентом связи, под которым понимают отношение взаимной индуктивности элементов цепи к корню квадратному из прои­зведения их собственных индуктивностей и.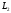

При составлении уравнений в случае наличия в цепи взаимо­связанных катушек следует иметь в виду, что напряжение на каждой такой катушке имеет несколько слагаемых.

Так для рис.23 напряжение между точками иравно

или в символической форме

Знак "минус" объясняется встречным включением катушек.

Рис. 23.

15. ПРИМЕР ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ

1. Для электрической цепи, показанной на рис.1 при

Рис.1.

определить токи и мощности ,,во всех ветвях и всей цепи. Расчет произвести методом проводимостей и символическим. Постро­ить полную векторную диаграмму.

РЕШЕНИЕ

Рис.2.

Для расчета цепи вначале определим индуктивные и емкостные сопротивления по формулам:

Осуществим анализ цепи методом проводимостей. Для этого преобразуем участок цели и перейдем от параллельной схемы к последовательной рис.3

Рис.3.

Рис.3.

Рис.3.

Рис.3.

Реактивная проводимость участка будет индуктивной, т.к.

Эквивалентный последовательный участок цепи будет:

Аналогично преобразуем участок цепи рис.4

Рис.4.

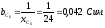
поэтому участок будет носить индуктивный характер.

После преобразования участка и электрическая цепь будет иметь вид: (Рис.5)

Рис. 5.

Полученную параллельную электрическую схему преобразуем в эквивалентную последовательную. (рис.6)

Рис.6.

Рис .6.

Рис. 6.

Рис. 6.

Полное сопротивление цепи:

Общий ток цепи будет равен (рис. 6):

Фазу приложенного напряжения примем равную нулю, тогда фаза общего тока цепи будет определяться:

По эквивалентной схеме видим, что цепь носит активно-индук-тивный характер, т.е. ток отстает по фазе от напряжения на угол . (Поэтому ставим знак ''минус''.)

Токи иопределим по схеме рис. 6 а

фазы токов и

Для определения токов ии их фази, необходимо вы­числить напряжениеи его фазу (рис.5).

Напряжение опережает по фазе токна уголт.к. учас­ток цепи носит активно-индуктивный характер.

Далее определим тoки ии иx фазы рис.2

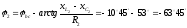
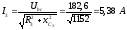
Ток опережает по фазе напряжениена угол(активно-емкостной характер ветви).

Для определения токов ,(рис.2) и их фаз вычислим напря­жение и его фазу (рис. 5):

Для построения полной векторной диаграммы необходимо вычислить напряжения на каждом сопротивлении (рис. 8)

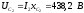
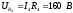
Определим активную P, реактивную Q и полную S мощности цепи.

Активная мощность всей цепи

Активные мощности отдельных ветвей равны:

, т.к.

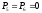, т.к.

Реактивная мощность всей цепи

Реактивные мощности отдельных ветвей

Полные мощности всей цепи и отдельных ветвей

2. Осуществим анализ цепи рис.2 символическим методом.

Для этого сопротивления ветвей электрической схемы рис.2 запишем в комплексной форме:

Ом

Ом

Ом

Рис.7.

Для определения общего комплексного сопротивления заданной элек­трической цепи вычислим комплексные сопротивления (рис.7)

и

где

Ом

После этого находим комплексный ток в неразветвленном участке цепи:

А

и комплексные токи в параллельных ветвях

А

А

Для определения комплексных токов исоответственно найдем напряжения

В

В

Полная комплексная мощность электрической цепи

,где - комплексный ток, сопряженный с

- активная мощность

- реактивная мощность

Вт Вар

То же самое находим для отдельных ветвей:

ВА

ВА

ВАр

Вт ВАр

ВА

Вт ВАр

ВА

Вт

ВА

ВАр

ВА

ВАр