8. Последовательное соединение r, l, c при переменном токе

Рис. 7.

По закону Ома для мгновенного значения напряжения

где - полное сопротивление цепи раcсчитывается по формуле

Угол сдвига фаз между приложенным напряжением и током

При последовательном соединении элемен­тов векторную диаграмму удобно начинать строить с вектора общего тока, а затем учитывая II закон Кирхгофа строим вектора напряжений рис.7.

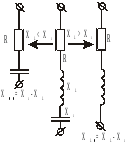
Рис. 8.

При последовательном соединении ,, реактивные сопротивления имож­но заменить одним эквивалентным, а характер цепи будет определяться по величине большего реактивного сопротивления рис. 8.

Реактивная мощность цепи ,,определяется:

Полная мощность

9. Параллельне соединения r и l в цепи переменного тока

Рис. 9.

Мгновенные значения напряжения и тока в неразветвленной цепи

,где- полная проводимость цепи

,где- активная проводимость

- реактивная проводимость индуктивности

Угол сдвига между приложенными напряжением и током

9. Параллельное соединение r с в цепи переменного тока

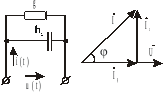
Рис. 10.

,

,

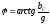
- реактивная проводимость ёмкости.

10. Параллельное соединение r , l , с в цепи переменного тока

Рис. 11.

,где

Полная проводимость определяется

Угол сдвига между напряжением и током

Для данной схемы соединения векторную диаграмму удобно начинать строить с вектора напряжения, а затем по 1 закону Кирхгофа (рис. 11)

При параллельном соединении R , L, С реактивные проводимости иможно заменить одной эквивалентной, а характер цепи будет определяться по величине большей реактивной про­водимости(рис.12)

Замена последовательного соединения активных и реактивных сопротивлений в параллельно соединенные активные и реактивные проводимости и обратно: (Рис .13)

,

,

,

,

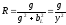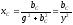
11. Анализ электрической цепи переменного тока методом проводимостей

Для расчетов токов I1,I2,I3 методом проводимостей в цепи (рис.14) необходимо перейти от разветвленной сложной схемы к простейшей последовательной цепи и определить ток в неразветвленном участке цепи I1, а затем в обратном порядке опре­делим токи в параллельных ветвях I2 и I3.

Рис. 14.

Преобразуем параллельный участок bc в последовательный. Для этого определим активные проводимости ,и реактив­ныеи(Рис.15)

Рис. 15.

При параллельном соединении участка эквивалентная актив­ная проводимость равна

При двух реактивных проводимостях разного характера, харак­тер эквивалентный проводимости будет той, реактивная прово­димость которая больше и будет равна разности проводимостей. Например,, тогда

Схема (рис 15) примет такой вид (рис.16)

Рис. 16.

Далее перейдем от проводимостей и к последователь­но соединенным сопротивлениям и(рис17)

Рис.17.

Данная разветвленная схема примет вид последовательно соединенных элементов (рис.18)

Рис. 18

При последовательном соединении активных сопротивлений эквивалентное активное сопротивление будет равно

а при двух или нескольких соединенных последовательно реак­тивных сопротивлений, характер эквивалентного сопротивления будет таким, реактивное сопротивление которое больше и будет равна разности сопротивлений.

Например,

тогда

Схема рис. 18 примет такой вид (рис. 19) и будет носить активно-емкостной характер

Рис. 19.

Полное сопротивление цепи

Ток в неразветвленном участке цепи

и фаза тока

Затем определим напряжение на участке

,где

фаза напряжения

Знак ''минус" показывает, что фаза напряжения при активно-

емкостном характере отстаёт от фазы тока (Рис.18). После этого можно определить токи в параллельных ветвях (Рис.14).

,где

фаза тока