Соединение трехфазного генератора ”звездой” при несимметричной нагрузке. Смещение нейтрали.
В данном случае:
(рисунок
4). Анализ трехфазной цепи в этом случае
легче сего осуществить методом двух
узлов. Действительно:
,
где
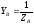
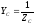
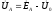
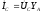
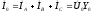
Векторная диаграмма показана на рисунке 8.
5
Рис.8
Из диаграммы видно, что система линейных напряжений симметрична, так как их значения определяются симметричной системой ЭДС. Из нее же можно заметить, что фазные напряжения не равны друг другу. Одни из фазных напряжений стали больше номинального значения, другие – меньше. Такое явление называется смещением нейтрали.
3
6
Для уменьшения влияния этого явления есть два способа:
обеспечение нагрузки по возможности ближе к симметричной;
уменьшение сопротивления нулевого провода.
Соединение трехфазного генератора и нагрузки ”треугольником”.
Будем по-прежнему исходить из симметричности трехфазного генератора.
; 
;
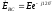Рассмотрим случай
симметричной нагрузки:
В этом случае
;
;
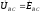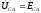
Таким образом, система фазных (они же линейные) напряжений образуют симметричную систему.
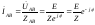
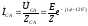
Видно, что система
фазных токов симметрична, причем
По первому закону Кирхгофа линейные токи равны:
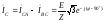
Видно, что и линейные
токи образуют симметричную трехфазную
систему, причем
Таким образом при
симметричной нагрузке и при соединение
”треугольником”
Векторная диаграмма для симметричной нагрузки показана на рисунке 9.
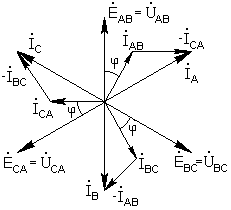
При несимметричной нагрузке анализ осуществляется аналогично симметричной нагрузке, но результат, естественно, будет другим.
Мощности в трехфазной цепи. Измерение мощности.
Под активной мощностью трехфазной цепи, по-прежнему, понимается средняя скорость потребления электрической энергии цепью.
Она может быть
найдена следующим образом:
где,
-
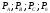активная мощность в цепи нулевого
провода и отдельных фаз.
Под реактивной мощностью понимается величина, пропорциональная средней скорости обмена энергией между нагрузкой и генератором.
Реактивная мощность трехфазной системы определяется как сумма реактивных мощностей фаз нагрузки и реактивной мощности нулевого провода.
Как и раньше полная мощность
и 
Однако, в отличии
от однофазных цепей, для трехфазных
угол
необязательно существует реально.
При симметричной нагрузке, очевидно, будет иметь:
;
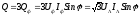
Для изменения мощности в трехфазной цепи можно включить три ваттметра, измеряющие активные мощности в каждой фазе
При этом, очевидно, что активная мощность трехфазной цепи равна сумме показаний трех ваттметров.
Для трехпроводной линии активная мощность трехфазной цепи может быть измеряна методом “двух ваттметров”, как показано на рисунке 10.
Рис.
10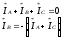
Докажем, что алгебраическая сумма показаний двух ваттметров равна активной мощности трехфазной цепи.
Получение вращающегося магнитного поля в трехфазных цепях.
8
Для получения вращающегося магнитного поля в трехфазной цепи достаточно взять три одинаковых, симметрично, т.е. под углом 120°, расположенных относительно друг-друга, катушки и подключить к трехфазному напряжению. (см. рисунок 11).
Рис.11
Углы между векторами индукции соответствующих катушек будут 120°. Так как индукция пропорциональна току, протекающему через катушку, то
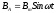
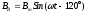
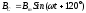
Выберем систему координат как показано на рисунке 11 и найдем сумму проекций векторов индукции на координатные оси.
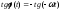
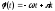
Дополнительное
исследование показывает, что реальной
ситуации отвечают только нечетные ” к
”. В простейшем случае
Для изменения вращения, реверса, достаточно поменять местами выводы любых двух катушек из трех.