VII. Дифференцирующие цепи.

В данной работе под дифференцирующей цепью будем понимать четырёхполюсник, напряжение на выходе которого пропорционально производной от входного напряжения, т.е.

Найдём частотные характеристики четырёхполюсника, обладающего указанными свойствами.

Пусть спектр входного напряжения задаётся функцией спектральной плотности . Входное напряжениепри этом, как известно, связано с его спектромобратным преобразованием Фурье:

Спектр выходного напряжения:

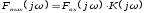, где

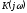комплексный коэффициент передачи четырёхполюсника по напряжению.

Выходное напряжение:

или

Ту же функцию 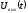найдём, подставив (2) в (1):

Т.к. переменные ω и t независимы, порядок следования операций дифференцирования и интегрирования по этим переменным можно изменить, т.е.:

Таким образом:

Сравнивая (3) и (4), получим:

Известно, что АЧХ и ФЧХ связаны с К(jω) следующим образом:

,

Следовательно, АЧХ и ФЧХ дифференцирующей цепи имеют следующий вид:

и

Графики этих функций показаны на рисунках 1 и 2.

Рис. 1 Рис. 2

Хотя реальные четырёхполюсники в точности подобных характеристик не имеют, при определённых условиях некоторые четырёхполюсники способны осуществлять приближённое дифференцирование. Например, четырёхполюсники, показанные на рис. 3 и 4, имеют комплексный коэффициент передачи:

, где постоянные времени равны:

для рис. 3

и для рис.4

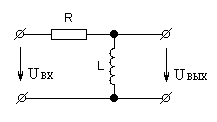
Рис. 3 Рис. 4

Для того, чтобы характеристика (6) приобрела вид (5), необходимо, чтобы

или

Т.к. для импульсных сигналов имеет место соотношение:

, где - длительность импульса, а- верхняя частота спектра этого импульса, то имеем:

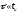
Последнее равенство можно рассматривать как условие, при котором схемы рис. 3 и 4 удовлетворительно дифференцируют импульсные сигналы.

Более высокое качество дифференцирования можно получить в схемах, использующих операционные усилители. На рис. 5 показана классическая схема дифференциатора.

Рис. 5

1. Интегрирующие цепи

Интегрирующая цепь – это четырёхполюсник, напряжение, на выходе которого пропорционально интегралу от входного напряжения, т.е.

Найдём комплексный коэффициент передачи по напряжению K(jω) такого четырёхполюсника.

Пусть спектр входного напряжения , тогда

Спектр входного напряжения:

Выходное напряжение:

Подставив (8) в (7), найдём выходное напряжение ещё раз:

Из-за независимости переменных t и ω порядок следования операций интегрирования по этим переменным можно изменить:

Таким образом:

Сравнивая (9) и (10) убеждаемся, что:

Зная К(jω), найдем АЧХ и ФЧХ интегрирующей цепи так же, как это было сделано для дифференцирующей цепи:

Графики этих функций показаны на рис. 6 и 7.

Рис. 6 Рис. 7

Приблизительно такие характеристики можно получить при определённых условиях в схемах рис. 8 и 9.