VI. Резонансные явления в электрических цепях Резонанс напряжений

Резонанс напряжений (или последовательный резонанс) может наблюдаться в электрической цепи, содержащей последовательно соединённые участки с разным характером реактивности. Название объясняется тем, что при резонансе оказываются равными друг другу по величине реактивные составляющие напряжений на указанных выше участках с разным характером реактивностей.

Резонанс напряжений может наблюдаться, к примеру, в цепи рис. 1.Найдём условие резонанса в этой цепи. Для этого участки R1 L и R2 C заменим эквивалентными (рис. 2).

Рис. 1

Как известно:

Если X’L окажется больше X’C, то цепь рис. 2 (а вместе с тем и цепь рис. 1) будет иметь активно-индуктивный характер и резонанс невозможен. Если X’L < X’C, то цепи рис. 1 и рис. 2 имеют активно-емкостной характер и резонанс также невозможен. При X’L = X’C цепи имеют чисто активный характер, следствием чего оказывается совпадение по фазе напряжения U и тока I, т.е. резонанс в цепи рис. 1.

Рис 2

С учётом (1) и (2) условие резонанса принимает вид:

Соотношение (3) приводит к уравнению третьей степени относительно частоты ω. Единственный положительный корень этого уравнения определяет так называемую резонансную частоту:

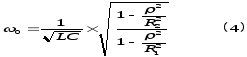
где – характеристическое сопротивление цепи.

Векторная диаграмма для цепи рис. 1 на резонансной частоте показана на рис. 3. Из диаграммы видно, что при резонансе, действительно, равны реактивные составляющие напряжений U1 и U2 .

U1p = U2p

Рис. 3

Рассмотрим интересный частный случай цепи рис. 1 при условии . Комплексное сопротивление такой цепи равно:

Таким образом, выяснилось, что комплексное сопротивление указанной цепи на всех частотах чисто активно. Это означает, что резонанс в данной цепи наблюдается на любой частоте.

Резонанс токов

Резонанс токов (или параллельный резонанс) может наблюдаться в электрической цепи, содержащей параллельно соединённые участки с разным характером реактивностей.

Название в этом случае объясняется тем, что при резонансе оказываются равными друг другу по величине реактивные составляющие токов указанных выше участков с разным характером реактивностей.

Резонанс токов может, к примеру, наблюдаться в цепи рис. 4

Условие резонанса для данной цепи можно найти аналогично тому, как это делалось для цепи рис. 1.

Рис. 4

Это условие имеет вид:

Решая это уравнение (5) относительно ω, найдём резонансную частоту:

Векторная диаграмма для цепи рис. 4 на резонансной частоте показана на рис. 5. Из неё видно, что при резонансе токов, действительно, равны по величине реактивные составляющие токов I1 и I2 .

I1p = I2p

Рис. 5

Точно так же, как и в предыдущем случае, можно доказать, что комплексное сопротивление цепи рис. 4 при условии

на любой частоте и равно: Z = R.

Это и означает, что и в этой цепи резонанс имеет место на всех частотах.