Типовые задачи рубежного контроля

1. Доказать тождество .

22. Доказать тождество .

23. Доказать тождество .

24. Доказать, что для любой функции fи любых множествAиBимеют место соотношения: а); б) .

25. Построить график и граф бинарного отношения , заданного на множестве, если .

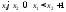26. Для бинарного отношения на множествепостроить графики отношений и .

27. Для бинарного отношения на множественайти, ,,,,.

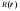28. Пусть бинарное отношение определено на множестве положительных рациональных чисел следующим образом:, если. Показать, что является отношением эквивалентности.

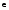29. Ассоциативна ли операция на множествеM, если, .

30. Решить уравнение в группе , если, ,.

31. Решить уравнениев группе, где.

32. Найти в решение системы уравнений

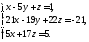
33. Доказать, что если в кольце оба произведения иобратимы, то оба элементаиобратимы. Что изменится в результате, если сохранить обратимость только одного произведения?

Модуль 2: Элементы теории графов Вопросы для подготовки к рубежному контролю

1. Основные понятия теории графов: неориентированные и ориентированные графы, цепи, пути, циклы, контуры, маршруты. Подграфы. Компоненты и бикомпоненты.

34. Деревья и их классификация. Теорема о числе листьев в полном p-дереве.

35. Методы систематического обхода вершин графа: поиск в глубину и поиск в ширину.

36. Поиск кратчайших расстояний от фиксированной вершины: алгоритм волнового фронта и поиск в ширину в орграфе с числовыми метками дуг.

37. Поиск фундаментальных циклов в неориентированном графе.

38. Гомоморфизм и изоморфизм графов. Группа автоморфизмов графа и ее вычисление.

39. Задача о путях в ориентированном графе, размеченном над полукольцом и ее решение с помощью алгоритма Флойда — Уоршелла — Клини. Задача о достижимости и поиске кратчайших расстояний между двумя узлами графа.

Типовые задачи рубежного контроля

1. Орграф задан матрицей меток дуг:

.

Используя поиск в ширину, найти кратчайшие расстояния от источника (вершины v₁), Показать изменение содержимого очереди вершин.

40. Для орграфа, используя алгоритм Дейкстры, найти кратчайшие расстояния от источника (вершины v₁), если орграф задан следующей матрицей меток дуг:

.

41. Для орграфа,используя решение систем линейных уравнений в полукольцеR⁺, вычислить матрицу кратчайших расстояний, если орграф задан следующей матрицей меток дуг:

.

42. Для орграфа, используя решение систем линейных уравнений в полукольце B, вычислить матрицу достижимости, если орграф задан следующей матрицей смежности вершин:

.

43. Найти группу автоморфизмов неориентированного графа, заданного матрицей смежности вершин.

.

44. Найти порядок группы автоморфизмов изображенного ниже графа

45. Для неориентированного графа, изображенного на рисунке, найти поиском в глубину фундаментальные циклы:

Модуль 3: Регулярные языки и конечные автоматы Вопросы для подготовки к рубежному контролю

1. Алфавит, слово, язык. Операции над языками, полукольцо всех языков в заданном алфавите и его замкнутость.

46. Регулярные языки и регулярные выражения.

47. Понятие конечного автомата (КА) и языка, допускаемого КА. Анализ и синтез КА.

48. Теорема Клини о совпадении класса языков, допускаемых КА и класса регулярных языков.

49. Детерминизация и минимизация КА. Регулярность дополнения регулярного языка и пересечения двух регулярных языков. Проблемы пустоты и эквивалентности.

50. Лемма о разрастании для регулярных языков.