Моментные ряды динамики

Уровни моментных рядов динамики характеризуют состояние изучаемого явления на определенные моменты времени. Каждый последующий уровень включает в себя полностью или частично предыдущий показатель. Так, например, число работников на 1 апреля 1999 г. полностью или частично включает число работников на 1 марта.

Если сложить эти показатели, то получим повторный счет тех работников, которые работали в течение всего месяца. Полученная сумма экономического содержания не имеет, это расчетный показатель.

В моментных рядах динамики с равными интервалами времени средний уровень ряда исчисляется по формуле средней хронологической:

• y -уровни моментного ряда;

• n -число моментов (уровней ряда);

• n — 1 — число периодов времени (лет, кварталов, месяцев).

Тренд – основная тенденция развития. Методы выявления тренда называются методами выравнивания временного ряда (метод наименьших квадратов, скользящей средней, конечных разностей).

Колебания, повторяющиеся через определенные промежутки времени или следующие известному циклу, называют периодическими колебаниями

Если даты регистрации или окончания периодов следуют друг за другом, то ряд динамики называется полным. Неполные ряды - когда принцип равных интервалов не соблюдается.

Абсолютными в статистике называются суммарные обобщающие показатели, характеризующие размеры, объемы, уровни, мощности, темпы и др. изменения величин. Абсолютные показатели являются именованными числами, т.е. измеримы.

Относительные статистические величины – это показатели в виде коэффициентов, характеризующих долю отдельных частей, изучаемой совокупности во всем ее объеме.

67. Основные показатели (характеристики) временных рядов (рядов динамики). Абсолютный прирост. Темп роста. Темп прироста. Цепные показатели и базисные показатели.

См пред вопрос

Абсолютные приросты (Δy) показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим или по сравнению с начальным уровнем. Формулы расчета можно записать следующим образом:

При уменьшении абсолютных значений ряда будет соответственно "уменьшение", "снижение".

Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим или по сравнению с начальным уровнем. Формулы расчета можно записать следующим образом:

Темпы роста показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим или по сравнению с начальным уровнем. Формулы расчета можно записать следующим образом:

Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим или по сравнению с начальным уровнем. Формулы расчета можно записать следующим образом:

Т_пр = Т_р - 100% или Т_пр= абсолютный прирост / уровень предшествующего периода * 100%

69. Сглаживание временных рядов (рядов динамики). Метод укрупненных интервалов. Скользящие средние.

Суть различных приемов сглаживания сводится к замене фактических уровней временного ряда расчетными уровнями, которые подвержены колебаниям в меньшей степени. Это способствует более четкому проявлению тенденции развития.

Укрупнение интервалов - наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней.

Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом:

При четных периодах скользящей средней можно центрировать данные, т.е. определять среднюю из найденных средних. К примеру, если скользящая исчисляется с продолжительностью периода, равной 2, то центрированные средние можно определить так:

Первую рассчитанную центрированную относят ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче на (m - 1)/2, где m - число уровней интервала.

71. Восстановленные значения и оценка точности восстановления функции методом наименьших квадратов. Критерий правильности расчетов.

В основе метода наименьших квадратов (МНК) лежит поиск таких значений коэффициентов регрессии, при которых сумма квадратов отклонений теоретического распределения от эмпирического была бы наименьшей. 

   

Иными словами, из всего множества линий, линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной: 

   

следовательно 

   

Целью процедур линейной регрессии является подгонка прямой линии по точкам. А именно, построить линию регрессии так, чтобы минимизировать квадраты отклонений этой линии от наблюдаемых точек. Поэтому на эту общую процедуру иногда ссылаются как на оценивание по методу наименьших квадратов. Прямая линия на плоскости (в пространстве двух измерений) задается уравнением Y=ax+b 

критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой при выравнивании ряда  гипотезы о характере распределения в эмпирическом ряду.

Эмпирические частоты получают в результате наблюдения. Теоретические частоты рассчитывают по формулам.

Для закона нормального распределения их можно найти следующим образом:

   

• Σƒ_i—сумма накопленных (кумулятивных) эмпирических частот 

• h — разность между двумя соседними вариантами

• σ — выборочное среднеквадратическое отклонение

• t–нормированное (стандартизированное) отклонение

• φ(t)–функция плотности вероятности нормального распределения (находят по таблице значений локальной функции Лапласадля соответствующего значения t)

Имеется несколько критериев согласия, наиболее распространенными из которых являются: критерий хи-квадрат (Пирсона), критерий Колмогорова, критерий Романовского.

Критерий согласия Пирсона χ²  – один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими (f_Т) и эмпирическими (f) частотами к теоретическим частотам:

   

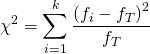
• k–число групп, на которые разбито эмпирическое распределение,  

• f_i–наблюдаемая частота признака в i-й группе,

• f_T–теоретическая частота.

72. Вероятностно-статистическая модель порождения данных в методе наименьших квадратов. Оценка остаточной дисперсии. Точечный и интервальный прогноз.

Метод наименьших квадратов Пусть дана система уравнений , где— некоторые функции,— некоторые известные значения, x — набор неизвестных (искомых) переменных. Для произвольных значенийзначенияотличаются от. Суть метода наименьших квадратов заключается в том, чтобы найти такие значения, при которых минимизируется сумма квадратов отклонений (ошибок):

Оценка остаточной дисперсии

Остаточная дисперсия — необъясненная дисперсия, которая показывает вариацию результата под влиянием всех прочих факторов, неучтенных регрессией

Точечный прогноз - единица измерения прогнозируемого показателя. Для получения данного прогноза необходимо в уравнение полученной кривой роста подставить требуемый прогнозируемый период t, значение которого определяется как t = n+1.

Интервальный прогноз - показатель, который рассчитывается на основе точечного, с указанием доверительного интервала.

73. Метод наименьших квадратов для модели, линейной по параметрам. Оценивание коэффициентов многочлена. Пакеты программ. Преобразования переменных.

Метод наименьших квадратов для модели, линейной по параметрам-см 72вопрос

Стандартным видом многочлена с одной переменной называется запись этого многочлена в порядке убывания степеней одночленов, каждый из которых записан в стандартном виде и среди которых нет подобных.

.

Числа называютсякоэффициентами многочлена. При этом .

74. Метод наименьших квадратов в случае нескольких независимых переменных (регрессоров). Оценивание параметров функции Кобба-Дугласа. Интерпретация результатов сравнения восстановленных и исходных значений производственной функции.

Метод наименьших квадратов в случае нескольких независимых переменных-см 72 вопрос

Оценивание параметров функции Кобба-Дугласа и интерпретация результатов сравнения

алгебраическая форма: N = A × L ^α   K^β ,

где N — национальный доход, A — коэффициент размерности, L, K — соответственно, объемы приложенного труда и капитала,   α и β  — константы (коэффициенты эластичности производства по труду L и капиталу K).

Функция однородная степени α+β; следовательно, увеличение L и K в одинаковое число раз m увеличивает доход в m^α+β раз. Если сумма α+β равна единице — функция линейно однородная; если больше или меньше единицы, имеет место эффект масштаба (соответственно, положительный или отрицательный).

75. Оценивание динамики потребительских цен на товары и услуги. Краткая история инфляции в России (1990-2012). Индивидуальные индексы. Весовые коэффициенты, задаваемые потребительской корзиной. Индекс потребительских цен (индекс инфляции).

Наиболее часто встречаются людям такие экономические характеристики, как цены на товары и услуги. Как правило, они изменяются с течением времени (динамика цен). Вполне естественно подвергнуть цены на товары и услуги эконометрическому анализу.

Под инфляцией понимается рост цен (крайне редко бывает, чтобы цены устойчиво падали). При анализе экономических процессов, протяженных во времени, необходимо переходить к сопоставимым ценам. Это невозможно сделать без расчета индекса роста цен, т.е. индекса инфляции. Проблема состоит в том, что цены на разные товары растут с различной скоростью, и необходимо эти скорости усреднять.

Краткая история инфляции в России (1990-2012)???

Индекс (лат. index – показатель, список) – статистический относительный показатель, характеризующий соотношение во времени (динамический индекс) или в пространстве (территориальный индекс) социально-экономических явлений. Речь идет о ценах на товары и услуги, объемах производства, себестоимости, объемах продаж и др.

В зависимости от степени охвата подвергнутых обобщению едениц изучаемой совокупности индексы подразделяются на индивидуальные(элементарные) и общие(сводные) .

Индивидуальные индексы характеризуют изменения отдельных единиц статистической совокупности. Так, например, если при изучении оптовой реализации продовольственных товаров определяются изменения в продаже отдельных товарных разновидностей, то получают индивидуальные (однотоварные) индексы.

Для конкретного товара рост цены описывается величиной (индивидуальным индексом):

Ii(t₁,t₂) = ri(t2)/ri(t1).

Эти индексы различны для различных товаров.

! Весовые коэффициенты, задаваемые потребительской корзиной.

Рассмотрим конкретного покупателя, т.е. конкретного экономического субъекта: физическое лицо, домохозяйство или фирму. Он покупает не один товар, а много. Обозначим через n количество типов товаров или услуг (далее кратко - товаров), которые он хочет и может купить. Обозначим через

Qi = Qi(t), i=1,2,...,n,

объемы покупок этих товаров по соответствующим ценам:

ri = ri(t), i=1,2,...,n

(имеется в виду цена за единицу измерения соответствующего товара - штуку или килограмм...).

Расходы на покупки рассматриваемого экономического субъекта равны:

Как свести к одной величине индексы цен для различных товаров и услуг?

Уровень цен выражается в виде индекса. Он является измерителем соотношения между совокупной ценой определенного набора товаров, называемого "рыночной корзиной" (или "потребительской корзиной"), для данного (текущего) момента времени, и совокупной ценой идентичной либо сходной группы товаров в базовый момент времени.

Мы усредняем индексы для отдельных товаров и услуг:

представляется естественным использовать взвешенное среднее арифметическое индексов роста цен на отдельные товары и услуги, а в качестве ВЕСОВ использовать относительные объемы потребления этих товаров и услуг. А именно, средним (или общим (сводным) индексом) роста цен за интервал времени [t₁,t₂] представляется естественным назвать величину

(1)

где С = Q₁(t₁) + Q₂(t₁) + Q₃(t₁)+ ...+ Q_n(t₁).

С - сумма объемов потребления Qi(t). При попытке ее расчета возникает необходимость складывать объемы потребления, выраженные в физических единицах измерения, например, килограммы картофеля складывать с буханками хлеба, бутылками молока, пачками сигарет и штуками холодильников.

Целесообразно измерять потребление не в физических единицах, а в стоимостных. Пусть

- доля потребления i-го продукта или услуги в общем потреблении C (в стоимостном выражении) - ВЕСОВОЙ КОЭФФИЦИЕНТ.

Определение 1. Индексом инфляции называется

Сравнение стоимостей потребительских корзин. Другой подход к измерению роста цен основан на сравнении стоимостей потребительской корзины (Q₁(t), Q₂(t), ..., Q_n(t)) в старых r_i(t₁), i=1,2,…,n, и новых r_i(t₂), i=1,2,…,n, ценах.

Определение 2. Индексом инфляции называется

76. Теорема умножения для индекса инфляции. Средний индекс (темп) инфляции. Годовая и среднемесячная инфляция.

Однако обычно индекс инфляции рассматривают для более или менее обширной совокупности экономических субъектов - для жителей региона или страны, предприятий определенной отрасли и т.д. В таких случаях Q_i(t) заменяют на общий объем потребления q_i(t), а r_i(t) - на среднюю цену p_i(t).

В этих обозначениях индекс инфляции имеет вид:

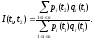
Соотношение индексов инфляции для трех моментов времени. Рассмотрим три момента времени t₁, t₂, t₃ и соответствующие индексы инфляции

и . Из определения индекса инфляции как отношения стоимостей потребительской корзины в соответствующие моменты времени вытекает следующее утверждение.

Теорема 3 (теорема умножения). Для любых трех моментов времени t₁, t₂, t₃ справедливо равенство

Средний индекс (темп) инфляции

Теорема умножения позволяет переходить от индексов инфляции за отдельные недели к индексам инфляции за месяц (четыре недели), от помесячных индексов инфляции - к квартальным и годовым, от годовых - к индексам инфляции за несколько лет.

Аналогично индекс инфляции за год равен произведению двенадцати индексов инфляции: за январь, февраль, март и остальные девять месяцев.

Среднемесячная инфляция, как и средний темп роста для любого временного ряда, рассчитывается в предположении, что ежемесячный рост цен не меняется от месяца к месяцу. Она равна:

то есть корень из 12

78. Применения индекса инфляции. Приведение к сопоставимым ценам. Реальные проценты платы за депозит. Реальные проценты платы за кредит. Оценка прожиточного минимума по методу Оршански. Курс доллара в сопоставимых ценах. Международные сопоставления на основе паритета покупательной способности.

Применения индекса инфляции.

Стоимость денежных единиц со временем меняется. Причем стоимость денежных единиц с течением времени, как правило, падает. Этому есть две основные причины – банковский процент и инфляция. В экономике есть инструменты для учета изменения стоимости денежных единиц с течением времени. Один из наиболее известных - расчет NPV (Net Present Value) - чистой текущей стоимости. Однако бухгалтерский учет и построенный на данных баланса предприятия экономический анализ финансово-хозяйственной деятельности предприятия пока что, как правило, игнорируют сам факт наличия инфляции. Обсудим некоторые возможности использования индекса инфляции в экономических расчетах.

Приведение к сопоставимым ценам.

Переход к сопоставимым ценам. Индекс инфляции предоставляет возможность перехода к сопоставимым ценам, расходам, доходам и другим экономическим величинам. Например, индекс инфляции за 4 года – (с 14.03.91 г. по 16.03.95 г.) – составил 5936. Это означает, что покупательной способности 1 рубля марта 1991 г. соответствует примерно 6000 (а точнее 5936) рублей марта 1995 г.

Рассмотрим приведение доходов к неизменным ценам. Пусть Иван Иванович Иванов получал в 1990 г. 300 руб. в месяц, а в мае 1995 г. - 1 млн руб. в месяц. Увеличились его доходы или уменьшились?

Номинальная заработная плата выросла в 1000000/300 = 3333 раза. Однако индекс инфляции на 18 мая 1995 г. составлял 7080. Это значит, что 1 руб. 1990 г. соответствовал по покупательной способности 7080 руб. в ценах на 18.05.95 г. Следовательно, в ценах 1990 г. доход И.И. Иванова составлял 1000000/7080 = = 142 руб. 24 коп., т.е. 47,4% от дохода в 1990 г.

Можно поступить наоборот, привести доход 1990 г. к ценам на 18 мая 1995 г. Для этого достаточно умножить его на индекс инфляции: доход 1990 г. соответствует 300 7080 = 2 млн 124 тыс. руб. в ценах мая 1995 г.

Реальные проценты платы за депозит.

Рассмотрим банк, честно выполняющий свои обязательства. Пусть он дает 10% в месяц по депозитным вкладам. Тогда 1 руб., положенный в банк, через месяц превращается в 1,1 руб., а через 2 – по формуле сложных процентов – в 1,12 = 1,21 руб., ..., через год – в 1,112 = 3,14 руб. Однако за год росли не только вклады, но и цены. Например, с 19.05.94 г. по 18.05.95 г. индекс инфляции составил 3,73. Значит, в ценах на момент оформления вкладов итог годового хранения равен 3,14 / 3,73 = = 0,84 руб. Хранение оказалось невыгодным – реальная стоимость вклада уменьшилась на 16%, несмотря на, казалось бы, очень выгодные условия банка.

Оценка прожиточного минимума по методу Оршански.

Минимальный прожиточный минимум оцениваем по методу М.Оршански с коэффициентом Энгеля 0,5. Этот метод основан на расчете стоимости минимальной продовольственной корзины и учете стоимостей остальных минимально необходимых затрат с помощью коэффициентов. Так, для "бедных семей" студентов МГИЭМ(ТУ) во время пробного бюджетного обследования в октябре-ноябре 1995 г. затраты на продовольствие составили 52% от всех расходов. Поэтому стоимость прожиточного минимума для них получим, приняв за 52% стоимость минимальной продовольственной корзины МГИЭМ, т.е. умножив ее стоимость на 1/0,52 = 1,92.

Метод М.Оршански предполагает, что структура затрат практически не меняется. Однако, как уже отмечалось, цены на промышленные товары и на услуги растут быстрее, чем на продовольствие. Поэтому замена 1,92 на 2,00 представляется обоснованной. Полученные значения (на май 1997 г. - 700 тыс. руб. в месяц на человека) хорошо согласуется с уже цитированными данными Московской федерации профсоюзов (750 тыс. руб.). Отметим, что для всей совокупности семей, чьи бюджеты были обследованы в 1996 г., затраты на продовольствие составили 42 %, т.е. для них коэффициент Оршански равен 1/0,42 = 2,38.

Курс доллара в сопоставимых ценах.

В июле 1995 г. индекс инфляции около 7000, а курс доллара США - около 4500 руб. за доллар. Следовательно, доллар США стоит 4500 / 7000 = 0,64 руб. в ценах 1990 г., т.е. примерно соответствует официальному обменному курсу в 1980-х годах. В сентябре 1994 г. курс доллара был около 2000, а индекс инфляции - около 2200, т.е. доллар стоил около 0,9 руб. в ценах 1990 г. Реальная покупательная способность доллара упала за 10 месяцев в 1,42 раза.

Ошибочно думать, что на Московской межбанковской валютной бирже курс доллара определяется по законам свободного рынка. На самом деле участвующие в торгах коммерческие банки административно зависят от Центрального Банка РФ. Другой инструмент влияния Центрального Банка - долларовые или рублевые интервенции. Реально курс доллара определяется руководством страны, действующим через Центральный Банк РФ. Одно из следствий реального понижения доллара - легальное присвоение средств тех граждан, которые пытаются сохранить свои сбережения (например на летний отдых), купив доллары США. Другой пример - спекулятивная инфляция, являющаяся следствием искусственного подъема курса доллара после "дефолта" августа 1998 г. Цель этой спекуляции очевидна - выжать рубли из населения с целью увеличения доходов государства (путем увеличения сбора налогов) и поддержки коммерческих банков, существенная часть активов которых "заморожена" в ГКО.

Международные сопоставления на основе паритета покупательной способности.

Индексы инфляции используются для пересчета номинальных цен в неизменные (сопоставимые). Другими словами, для приведения доходов и расходов к ценам определенного момента времени. Потребительские корзины для промышленных предприятий, конечно, должны включать промышленные товары, а потому отличаться от потребительских корзин, ориентированных для изучения жизненного уровня.

Валовой внутренний продукт, валовой национальный продукт и другие характеристики экономического положения страны рассчитываются в текущих ценах. Для перехода к неизменным ценам, грубо говоря, надо поделить на индекс инфляции (т.е. умножить на дефлятор).

Паритет покупательной способности (ППС) валют – соотно-

шение валют, обеспечивающее равенство оценок эквивалентно-

го набора товаров и услуг, исчисленных в соответствующих наци-

ональных ценах и валютах.

Паритет покупательной способности валют может быть рас-

считан как для отдельного товара или услуги, так и для любой их

группы, валового внутреннего продукта в целом.

79. Виды инфляции: спроса, издержек, административная.

Всегда говорят об инфляции спроса. Это ситуация, когда у населения много денег, которые оно хочет истратить. А товаров мало. Тогда цены растут. Либо непосредственно, либо через механизм " черного рынка".

Другой вид инфляции - инфляция издержек. Производитель вынужден повышать цену на свою продукцию, потому что его поставщики повышают цены на собственную продукцию. Этот порочный круг очень трудно разорвать.

Третий вид инфляции - административная инфляция. Цены повышает государство. Естественно, на то, что оно контролирует. Например, с августа по декабрь 1998 г. курс доллара США был поднят в 4 раза. Последствия были понятные: адекватный подъем цен на импортные товары, рост цен на продукцию, для изготовления которой использовались импортные комплектующие, а затем и рост цен на чисто отечественную продукцию, если такая вообще существует. В результате инфляция за год составила 80%.

Выше уже приводились примеры административного регулирования цен. Политика государственных органов в области энергетики, транспорта, экспорта и импорта и других сфер государственного регулирования экономики оказывает непосредственное влияние на инфляцию.

80. Примеры инфляционных процессов в различных странах и в различные времена.

В мире почти нет стран, где бы во второй половине XX в. не существовала инфляция. Она как бы пришла на смену прежней болезни рыночной экономики, которая стала явно ослабевать, - циклическим кризисам. Инфляция была характерна для денежного обращения: России - с 1769 до 1895 г. (за исключением периода 1843 - 1853 гг.); США - в период войны за независимость 1775 - 1783 гг. и гражданской войны 1861 - 1865 гг. Англии - во время войны с Наполеоном в начале XIX в.. Франции - в период Французской революции 1789 - 1791 гг. Особенно высоких темпов инфляция достигла в Германии после первой мировой войны, когда осенью 1923 г. денежная масса в обращении достигала 496 квинтиллионов марок, а денежная единица обесценилась в триллион раз.

Приведенные исторические примеры доказывают, что инфляция не является порождением современности, а имела место и в прошлом.

Современной инфляции присущ ряд отличительных особенностей: если раньше инфляция носила локальный характер, то сейчас - повсеместный, всеохватывающий; если раньше она охватывала больший и меньший период, т.е. имела периодический характер, то сейчас - хронический; современная инфляция находится под воздействием не только денежных, но и неденежных факторов. Следовательно, современная инфляция испытывает воздействие многих факторов.

Существует несколько видов инфляции. Прежде всего те, которые выделяют с позиции темпа роста цен (первый критерий), т.е. количественно: 1. Ползучая (умеренная) инфляция, для которой характерны относительно невысокие темпы роста цен, примерно до 10% или несколько больше процентов в год. Такого рода инфляция присуща большинству стран с развитой рыночной экономикой, и она не представляется чем-то необычным. Данные за 70-е, 80-е и начало 90-х гг. по США, Японии и западноевропейским странам, как раз и говорят о наличии ползучей инфляции. Средний уровень инфляции по странам Европейского сообщества составил за последние годы около 3-3,5%; 2. Галопирующая инфляция (рост цен на 20—2000% в год). Такие высокие темпы в 80-х гг. наблюдались, к примеру, во многих странах Латинской Америки, некоторых странах Южной Азии. По подсчетам Центрального банка России, индекс потребительских цен в нашей стране в 1992 г. поднялся до 2200%. 3. Гиперинфляция - цены растут астрономически, расхождение цен и заработной платы становится катастрофическим, разрушается благосостояние даже наиболее обеспеченных слоев общества, бесприбыльными и убыточными становятся крупнейшие предприятия (МВФ за гиперинфляцию сейчас принимает 50%-й рост цен в месяц).

Так, в Аргентине на апрель 1990 г. зафиксирован рост цен в 200 раз (темп роста инфляции -- 2000 %). Спасло аргентинцев лишь то, что у них преобладает натуральное сельское хозяйство и без рыночных отношений можно прожить некоторое время.

Недавний рекорд принадлежит Никарагуа: за период гражданской войны среднегодовой прирост цен достигала 33000%.

Наиболее ошеломляющим в истории является пример гиперинфляции в Венгрии в 1946 г., когда довоенный форинт (денежная единица Венгрии) стоил 829 октильонов новых форинтов (единила с 22 нулями), а доллар США обменивался на 3*1022 форинтов.

81. Индекс – показатель сравнения двух состояний одного и того же явления. Индивидуальный индекс. Сводный (общий) индекс. Отчетные данные и базисные данные. Индекс как показатель центральной тенденции (индекс средний из индивидуальных). Примеры.

Индекс — это показатель сравнения двух состоянии одного и того же явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов).

Каждый индекс включает два вида данных: оцениваемые данные, которые принято называть отчетными и обозначать значком «1», и данные, которые используются в качестве базы сравнения, — базисные, обозначаемые значком «О». Индекс, который строится как сравнение обобщенных величин, называется сводным, или общим, и обозначается I. Если же сравниваются необобщенные величины, то индекс называется индивидуальным и обозначается i.

Вы можете услышать, что уровень потребительских цен понизился или повысился. Речь в этом случае идет об индексе цен на потребительские товары. Общее изменение образуется под влиянием изменений цен на отдельные товары. Таким образом, мы имеем ряд отношений:

Индекс цен для каждого товара должен сопровождаться неким «весом», который позволяет оценить относительную значимость этого индекса для потребителя. В качестве веса используют удельный вес в общей стоимости покупок в базисном периоде:

2 ВАРИАНТ

Помимо записи общих индексов в агрегатном виде, на практике часто используют формулы их расчета как величин, средних из соответст­вующих индивидуальных индексов.

Используя их формулы, можем записывать, что q₁ = q₀i_q и p₁ = p₀i_p, а также, что q₀ =q₁/i_q и р₀=р₁/i_p. Подставив от­четные значения количества товара и цены в формулу общего индекса выручки, получим

I_Q===.(1)

Значит, общий индекс выручки можно определять только через ее базисные значения с умножением в числителе на индивидуальный ин­декс выручки по конкретному товару.

Теперь подставим базисные значения количества товара и цены в формулу общего индекса выручки. Тогда получим

I_Q =.(2)

Значит, общий индекс выручки можно определять только через ее отчетные значения с делением в знаменателе на индивидуальный ин­декс выручки по конкретному товару.

Аналогично через индивидуальные индексы количества товара и це­ны можно выразить агрегатные общие индексы Ласпейреса и Пааше.

82. Индексы Ласпейреса, Пааше, Ирвинга Фишера.

Индексы цен показывают, как изменилась стоимость продукции за счет изменения цен.

Агрегатный индекс цен Пааше:

, (7.8)

где p₁q₁ – фактическая стоимость продаж (товарооборот) в отчетном периоде;

p₀q₁ – условная стоимость товаров, реализованных в отчетном периоде по базисным ценам.

Агрегатный индекс цен Ласпейреса:

, (7.9)

где p₀q₀ – фактическая стоимость продаж (товарооборот) в базисном периоде;

p₁q₀ – условная стоимость товаров, реализованных в базисном периоде по отчетным ценам.

Индекс цен Пааше показывает изменение цен отчетного периода по сравнению с базисным (на сколько товары стали дороже (дешевле)). Если бы товары были реализованы в отчетном периоде по базисным ценам, то фактическая экономия составила

. (7.10)

Индекс цен Ласпейреса показывает условную экономию, т.е. на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде. Этот индекс применяется при прогнозировании объема товарооборота в связи с предлагаемым изменением цен.

В условиях стабильности применяют индекс Пааше, при инфляции – индекс Ласпейреса.

Основываясь на рассмотренных двух вариантах построения индексов, Фишер предложил рассчитывать среднюю геометрическую индексов цен Пааше и Ласпейреса:

. (7.11)

Этот индекс носит название “идеальный” индекс цен Фишера. Индекс цен Фишера “обратим” во времени (т.е. если рассчитывать индекс базисного периода к отчетному, он будет равен обратной величине первоначального индекса), но лишен экономического содержания.