
- •16.Изгиб с кручением. Расчетные формулы по различным теориям.
- •18.Рассчет осесимметричных оболочек по безмоментной теории. Уравнение Лапласа.
- •20. Расчет толстостенных цилиндров. Общее решение задач Ламе.
- •20. Нагружение цилиндра внутренним давлением.
- •21. Нагружение цилиндра внешним давлением.
- •22. Понятие о механике разрушения. Модель тела с трещинами.
- •24. Понятие устойчивости деформируемой системы.
- •25. Устойчивость сжатых стержней. Задача Эйлера.
24. Понятие устойчивости деформируемой системы.
Не
все теоретически возможные равновесные
формы могут быть реализованы в
действительности. Реальный объект
всегда отличается от расчетной схемы.
Всегда имеются неучтенные в расчетной
схеме силы, реальная геометрическая
форма всегда отклоняется от проектной.
Имеются отклонения в свойствах материалов
от того, что предусматривалось проектом
и т. д. В некоторых случаях эти, казалось
бы второстепенные факторы могут привести
к тому, что теоретически возможное
состояние практически становится
неустойчивым. Например, никто не видел
следующей картины: идеально прямой
карандаш стоит строго вертикально на
горизонтальном идеально гладком стекле.
В этом случае реакция опорной поверхности
направлена строго вертикально и равняется
весу карандаша. Две равные по величине
действующие по одной прямой и направленные
в противоположные стороны силы, должны
уравновешиваться, однако данное
равновесное состояние реализовать в
действительности невозможно. Помимо
веса карандаша и реакции поверхности
будут действовать и другие силы, например
силы обусловленные движением воздуха,
карандаш не будут строго прямолинейным,
а поверхность стекла совершенно
горизонтальной и идеально гладкой и т.
д.Будем называть неучтенные силы,
отклонения в геометрической форме и т.
д., возмущениями.Определение:
будем
называть равновесное состояние
устойчивым, если оно мало изменяется
при малых возмущенияхПр:
Картину разрушения образца при при
растяжении с образованием шейки можно
характеризовать, как потерю устойчивости
цилиндрической формы образца.По мере
приближения состояния образца к точке
С цилиндрическая форма образца становится
неустойчивой, образуется шейка и малым
изменениям силы соответствуют значительные
изменения конфигурации
системы.

25. Устойчивость сжатых стержней. Задача Эйлера.
Равновесное
состояние устойчивым, если оно мало
изменяется при малых возмущениях.Рассмотрим
центрально сжатый шарнирно закрепленный
с обоих концов стержень. Необходимо для
этого стержня найти критическую
силуПрямолинейная равновесная форма
возможна (v
= 0).Допустим, что наряду с прямолинейной
равновесной формой возможна и криволинейная
равновесная форма, показанная на рисунке.
Кривизна
стержня на основании закономерности
известной из теории изгиба выразится
 Будем
полагать, что угол поворотаv’
– величина малая по сравнению с единицей
и тем более мал квадрат этой величины
по с равнению с единицей, тогда
Будем
полагать, что угол поворотаv’
– величина малая по сравнению с единицей
и тем более мал квадрат этой величины
по с равнению с единицей, тогда

Изгибающий
момент в произвольном сечении координатой
z
 (знак минус увязывает знак прогиба
и момента).
(знак минус увязывает знак прогиба
и момента).
Дифференциальное уравнение изогнутой оси выглядит
 или
или
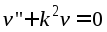 ,
где
,
где (1)Решение этого дифференциального
уравнения, как известно
(1)Решение этого дифференциального
уравнения, как известно
 Из
граничных условий попробуем найти
произвольные постоянные
Из
граничных условий попробуем найти
произвольные постоянные
 и
и
1)
при z
= l
v=0

2)
при z
= 0 v
=0

Возможны две ситуации
 .
Откуда v
= 0, т.е. получаем прямолинейную равновесную
форму
.
Откуда v
= 0, т.е. получаем прямолинейную равновесную
форму


подставим
в (1) выражение

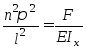 ,
откуда
,
откуда
найдем выражение силы, при которой помимо прямолинейной равновесной формы, появляется сложная криволинейная равновесная форма
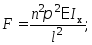 реальный
смысл имеет наименьшее значение силы
при
реальный
смысл имеет наименьшее значение силы
при
 Эйлерова сила – критическая сила
Эйлерова сила – критическая сила
Очевидно,
что
 -
минимальный момент инерции.
-
минимальный момент инерции.
Потеря
устойчивости будет происходить по
синусоиде

26.Влияние
условий закрепления на величину
критической
силы.Формула
 дает возможность определить критическую
силу только в случае шарнирного опирания
обоих концов стержня. Обобщим полученный
результат на некоторые другие часто
встречающиеся случаи закрепления.
дает возможность определить критическую
силу только в случае шарнирного опирания
обоих концов стержня. Обобщим полученный
результат на некоторые другие часто
встречающиеся случаи закрепления.
а) Стержень, закрепленный жестко одним концом и свободный от закрепления на другом.Очевидно, изгиб стержня в этом случае будет таким же, как и в случае шарнирно опертого стержня, но имеющего длину в 2 раза большую.
Критическая
сила в этом случае будет равна критической
силе шарнирно опертого стержня, имеющего
длину


Введем
понятие коэффициента приведения длины
-
 ,
т.е. числа показывающего во сколько раз
нужно увеличить длину шарнирно опертого
стержня, чтобы критическая сила для
него равнялась критической силе стержня
длиной
,
т.е. числа показывающего во сколько раз
нужно увеличить длину шарнирно опертого
стержня, чтобы критическая сила для
него равнялась критической силе стержня
длиной при заданном закреплении. Очевидно,
что в нашем случае
при заданном закреплении. Очевидно,
что в нашем случае .
.

Коэффициент
 можно трактовать как число, показывающее
сколько раз длина стержня укладывается
в длине полуволны синусоиды, по которой
происходит потеря устойчивости.
можно трактовать как число, показывающее
сколько раз длина стержня укладывается
в длине полуволны синусоиды, по которой
происходит потеря устойчивости.
Обобщим
формулу Эйлера

27.
Пределы применимости формулы Эйлера.
Формула
Эйлера
выведена в предположении, что материал
линейно упруг, и , естественно, применима
в тех случаях пока справедлив закон
Гука.Придадим формуле
 иной вид.Введем понятие критического
напряжения, т.е. напряжения соответствующего
критической силе
иной вид.Введем понятие критического
напряжения, т.е. напряжения соответствующего
критической силе
 но
но

где
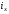 - минимальный радиус инерции сечения.Введем
еще одну величину – гибкость стержня
- минимальный радиус инерции сечения.Введем
еще одну величину – гибкость стержня
 тогда
тогда Тогда
можно сказать, что формула Эйлера
справедлива, если критические напряжения
не превышают предела пропорциональности
при
Тогда
можно сказать, что формула Эйлера
справедлива, если критические напряжения
не превышают предела пропорциональности
при
сжатии.

Выясним,
при каких гибкостях можно использовать
формулу Эйлера.Приравняем в (4)


Если
 то можно использовать формулу (3).
то можно использовать формулу (3).
Для
малоуглеродистых сталей, особенно часто
используемых для сжатых элементов: тогда
тогда
 т.е.
для малоуглеродистых сталей формулу
Эйлера можно использовать при гибкостях
больших 100.
т.е.
для малоуглеродистых сталей формулу
Эйлера можно использовать при гибкостях
больших 100.
Приведенное
выше решение пригодно только для
сравнительно длинных и тонких стержней.
В случае более коротких и жестких
стержней потеря устойчивости происходит
при возникновении пластических
деформаций, и задача требует специального
рассмотрения. Существуют решения
(Т.Карман, Энгессер) об устойчивости
стержня за пределами упругости. Иногда
прибегают к эмпирическим формулам типа
формулы Ясинского
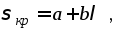 где
где
 и
и
 - константы, зависящие от свойств
материала.
- константы, зависящие от свойств
материала.
