
- •1.Предельный момент для сечения при изгибе
- •2. Расчет балок по методу предельных нагрузок
- •3.Напряжение. Понятие напряженного состояния
- •8.Определение главных напряжений в случае, когда известно положение одной из главных площадок.
- •9.Классификация напряженных состояний
- •10. Тензор деформаций. Связь между компонентами тензора деформаций и компонентами вектора перемещений.
- •11. Обобщенный закон Гука
- •12. Понятие о предельном напряженном состоянии (критерии пластичности и разрушения). Эквивалентное напряжение.
- •13. Теория наибольших касательных напряжений (Треска – Сен-Венана).
8.Определение главных напряжений в случае, когда известно положение одной из главных площадок.
Пусть

главное напряжение (Рис.11). Требуется
найти два другие главные напряжения.
Воспользуемся круговой диаграммой
Мора. Площадкам 1 и 2 соответствуют точки
на координатной плоскости
главное напряжение (Рис.11). Требуется
найти два другие главные напряжения.
Воспользуемся круговой диаграммой
Мора. Площадкам 1 и 2 соответствуют точки
на координатной плоскости
 .
Нанесём их и проведём окружность,
проходящую через эти точки, центр которой
лежит на оси
.
Нанесём их и проведём окружность,
проходящую через эти точки, центр которой
лежит на оси .
Точки пересечения окружности и оси
.
Точки пересечения окружности и оси дадут значения главных напряжений
дадут значения главных напряжений и
и .
Найдём их. Координата центра окружности
равна
.
Найдём их. Координата центра окружности
равна
 Радиус
окружности:
Радиус
окружности:
 .
.


Тогда

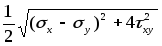 .
.
Мы
получили нам уже знакомую формулу,
выведенную для случая плоского
напряжённого состояния. Напряжение
 не влияет на два других главных напряжения.
Сопоставляя
не влияет на два других главных напряжения.
Сопоставляя ,
, и
и ,
устанавливаем
,
устанавливаем .
.
9.Классификация напряженных состояний
В зависимости от числа главных напряжений отличных от нуля напряжённые состояния бывают:
1.1) Трёхосные или объёмные напряжённые состояния – случай, когда ни одно из главных напряжений не равно нулю.
1.2)
Напряжённое состояние называется
двухосным
или плоским,
если только два главных напряжения
отличны от нуля. В этом случае кубический
инвариант
 равен нулю. Характеристическое уравнение
принимает вид
равен нулю. Характеристическое уравнение
принимает вид
 Одно
из главных напряжений равно нулю, а два
других определяются из решения
приведенного выше квадратного уравнения.
Если напряженное состояние задано
напряжениями по площадкам, одна из
которых, например, с внешней нормалью
Одно
из главных напряжений равно нулю, а два
других определяются из решения
приведенного выше квадратного уравнения.
Если напряженное состояние задано
напряжениями по площадкам, одна из
которых, например, с внешней нормалью
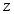 ,
является той главной площадкой, по
которой главное напряжение равно нулю,
то тензор напряжений принимает вид
,
является той главной площадкой, по
которой главное напряжение равно нулю,
то тензор напряжений принимает вид
 Инварианты
напряжённого состояния примут вид:
Инварианты
напряжённого состояния примут вид:
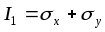 ,
, .
Подставляя это в выражение для главных
напряжений, получим формулу
.
Подставляя это в выражение для главных
напряжений, получим формулу
 .(1.6)
.(1.6)
1.3)
Если кубический
 и квадратичный инвариант одновременно
равны нулю, то лишь одно главное напряжение
отлично от нуля. Оно называетсяодноосным
или линейным
и возникает, например, при растяжении
и сжатии при чистом изгибе.
и квадратичный инвариант одновременно
равны нулю, то лишь одно главное напряжение
отлично от нуля. Оно называетсяодноосным
или линейным
и возникает, например, при растяжении
и сжатии при чистом изгибе.
В зависимости от знаков главных напряжений:
2.1:Трёхосные
растяжения, когда ни одно из главных
напряжений не является сжимающим.
2.2:Трёхосные сжатия, когда ни одно из
главных напряжений не является
растягивающим. 2.3:Смешанные напряжённые
состояния, когда
 и
и имеют разные знаки.
имеют разные знаки.
10. Тензор деформаций. Связь между компонентами тензора деформаций и компонентами вектора перемещений.
Деформированное
состояние в точке определено, т.е. можно
вычислить удлинение по любому направлению,
проходящему через данную точку, если
задан тензор деформаций. Тензор
деформаций - совокупность
удлинений по трём взаимно перпендикулярным
направлениям и углов сдвига в плоскостях
трёх площадок, нормальных к данным
направлениям. Он имеет вид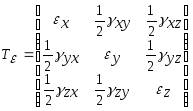
Здесь:

деформации относительного удлинения
в направлении соответствующих осей;
деформации относительного удлинения
в направлении соответствующих осей;

деформации сдвиг в соответствующих
координатных плоскостях. Тензор
деформаций симметричен. Теория
деформированного состояния аналогична
теории напряжённого состояния.
деформации сдвиг в соответствующих
координатных плоскостях. Тензор
деформаций симметричен. Теория
деформированного состояния аналогична
теории напряжённого состояния.
Рассмотрим
малый элемент, который в процессе
деформации изменил свою конфигурацию.
Деформация в направлении оси

 .
.

 .
.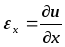 ;
;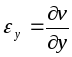 ;
; ;
;
 ;
;
 ;
; .
.
