РК6-93.АОРС.ПугачёвАВ

Московский государственный технический университет имени Н.Э. Баумана

РЕФЕРАТ

по курсу

«Методы оптимизации»

на тему:

«Алгоритм оптимизации роем светлячков»

Выполнил: Пугачёв А.В.

группа РК6-93

Проверил: Карпенко А.П.

Москва, 2014

Оглавление

Введение ................................................................................................................... 3

1. Краткие сведения ............................................................................................... 4

2. Постановка задачи ............................................................................................. 5

3. Алгоритм динамического симплекса ................................................................ 6

   1. Описание алгоритма ..................................................................................... 6

   2. Выбор параметров в динамическом симплекс-методе ............................... 8

   3. Примеры ........................................................................................................ 8

      1. Двухмерная задача динамической непрерывной оптимизации ........... 8

      2. Трехмерная задача динамической непрерывной оптимизации.......... 10

   4. Вывод о модификации................................................................................ 11

Заключение ............................................................................................................. 12

Список литературы ................................................................................................ 13

Введение

Для решения динамических задач оптимизации на сегодняшний день разработано множество алгоритмов.

В реферате осуществлен обзор статьи, посвященной динамическим задачам непрерывной оптимизации. В разделе 1 дано описание используемых в статье терминов [1], в разделе 2 приведена постановка задачи [1], в разделе 3 изложено описание алгоритма (модификация симплекс-метода Нелдера-Мида)

[1] и примеры его применения.

1. Краткие сведения

Алгоритм оптимизации роем светлячков (GSO -GLOWWORM SWARM OPTIMIZATION ALGORITHM) предложили в 2005 г. Кришнананд (K.N. Krishnanand) и Гхоус ( D. Ghose).

Динамические задачи оптимизации (DOPs – Dynamic Optimization Problems) — задачи, где технические характеристики (часто известные в оптимизации как фитнес-функции) изменяются с течением времени в процессе оптимизации, что приводит к непрерывному движению оптимума.

Целевая функция — математическое выражение некоторого критерия качества одного объекта (решения, процесса и т.д.) в сравнении с другим. Требуется найти такие оценки, в которых целевая функция достигнет минимума.

Задачи непрерывной оптимизации — задачи, в которых целевая функция и ограничения непрерывно зависят от переменных.

2. Постановка задачи

Общая нелинейная изменяющаяся во времени система и ее целевая функция имеет вид

, (1) (2) где f и g являются нелинейными функциями, х – входные процессы, - изменяющийся во времени вектор параметров, у – выходные процессы, _ - шум, J является целевой функцией, которая должна быть сведена к минимумуf[1].

В режиме моделирования новое значение у рассчитывается путем оценки функции f. В режиме реального времени у получают в виде измерения. Значение функции и измерение взаимозаменяемы в статье [1]. Каждое измерение y занимает некоторый конечный промежуток времени. Таким образом, проблема, с которой мы сталкиваемся, состоит в том, чтобы оптимизировать функцию y, используя как можно меньше оценок (измерений) функции.

3. Алгоритм динамического симплекса

Алгоритм динамического симплекса (Dynamic simplex), разработанный авторами статьи [1], основан на симплекс-методе Нелдера-Мида. Данный алгоритм позволяет отслеживать движущийся оптимум.

3.1 Описание алгоритма

Состояние светлячка , i ϵ [1: |S|], определяют следующие переменные:

X_i – его текущие положение в пространстве поиска

l_i – уровень светимости (luciferin level)

r_i – радиус окрестности (neighborhood range)

Основным содержанием каждой итерации является обновление значений указанных переменных.

Уровень светимости светлячка s_i обновляем по формуле:

­_­­l_iʹ=(1-ρ) l_i +γφ (X_i), i ϵ [1: |S|],

где ρ, γ –положительные свободные параметры алгоритма, моделирующие распад флуоресцирующего вещества и привлекательность светлячка. Отличные от нуля значения параметра ρ обеспечивают алгоритм памятью. Параметр γ определяет относительные веса текущей светимости агента и значения его фитнесс-функции.

Светлячок s_j считается соседом светлячка :

i, j ϵ [1: |S|], i ≠ j

при выполнении двух следующих условий:

• евклидово расстояние между этими светлячками не превышает текущий радиус окрестности r_i

• текущий уровень светимости светлячка s_j превышает этот уровень светлячка , т.е. l_j ­> l_i.

Если светлячок имеет несколько соседей, то случайным образом выбирает одного из них с вероятностью, пропорциональной уровням их светимости (правило рулетки).

Положим, что по рассмотренной схеме светлячком выбран . Тогда новое положение светлячка определяет формула:

где - постоянное значение шага(свободный параметр алгоритма).

Новый радиус окрестности светлячка s_i определяем в соответствии с выражением:

где – текущее множество соседей светлячка , -минимально допустимый радиус окрестности, -желательное число соседей, - положительная константа. Последние три величины являются свободными параметрами алгоритма.

Модификации.

Рассмотрим некоторые модификации представленного канонического алгоритма GSO.

Для диверсификации поиска в случае, когда число соседей светлячка , в окрестности менее желательного числа n, радиус окрестности может быть по тому или иному правилу расширен (в простейшем случае, положим, на 5%).

В той же ситуации возможно иное решение – случайное перемещение светлячка в переделах куба с центром в точке 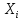и длиной ребра, равное шагу :

Если значение фитнесс функции в новой точке лучше ее значения в точке , то оставляем светлячка в точке .

Новый радиус окрестности светлячка может вычисляться не по формуле

а по формуле вида

где - максимальное значение этой величины, – заданная константа, – средняя текущая плотность агентов в окрестности :

Величины , представляют собой свободные параметры алгоритма.

Наиболее сложной является модификация алгоритма GSO, использующая специальный механизм организации агентов в группы. В каждой из групп в этом случае выделяют одного из агентов в качестве ее владельца (master), который определяет миграцию всех подчиненных (slave) агентов. В исходном состоянии подчиненные агенты равномерно распределены случайным образом в гиперсфере радиуса с центром, совпадающим с начальным положением владельца группы. В процессе поиска величина может варьироваться в диапазоне, где - свободный параметр.