утс

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Московский государственный технический университет имени Н.Э. Баумана»

МГТУ им. Н.Э. Баумана

Факультет “Энергомашиностроение”

Домашнее задание №1

по курсу

«Управление техническими системами»

Вариант 1(15)

Студент: Анищенко Ю.В.

Группа: Э8-72

Преподаватель: Трифонов В.Л.

Москва , 2014

Исследование электродуговой системы как объекта управления

Цель задания – получить математическое описание электродуговой системы в стандартной для теории управления форме, определить устойчивость установившихся режимов, построить статические и динамические характеристики электродуговой системы как объекта управления.

Исходные данные

Электрические параметры цепи

Е0, В	R0, Ом	L, Гн	k0, ВА
400	0,8	0.01	30000

Порядок выполнения задания

1. Построить реостатную характеристику цепи(РХЦ) и ВАХ дуги.

2. По статическим характеристикам цепи и дуги (точки 1 и 2) найти устойчивый режим горения дуги. Подсчитать фактор устойчивости на обоих режимах

Фактор устойчивости определяется по формуле:

где – ток установившегося режима.

В точке 1 , F < 0, неустойчивый режим.

В точке 2 , F > 0, устойчивый режим.

3. Получить линейное математическое описание электрической цепи с дугой: линейное дифференциальное уравнение, передаточные функции, структурную схему в соответствии с функциональной схемой. В качестве выходной координаты рассматривается относительное изменение тока y=Δi/i₀, в качестве входных координат – относительные изменения активного сопротивления цепи z=ΔR/R₀ и ЭДС f=ΔE/E₀ (i₀, R₀ и U₀=i₀R₀ – значения параметров цепи на устойчивом режиме дуги).

Электрическое уравнение цепи с дугой:

В устойчивом режиме ток не изменяется, поэтому

4

Выразим абсолютные значения параметров цепи через отклонения от устойчивого режима:

Подставим в электрическое уравнение цепи с дугой и найдем линейное дифференциальное цепи с дугой в отклонениях от устойчивого режима:

Поделим получившееся уравнение на , чтобы получить уравнение в относительных единицах:

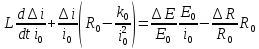
Подставим обозначения для фактора устойчивости и относительные изменения параметров:

Введем обозначения – постоянная времени, c; – коэффициент усиления передачи по напряжению; – коэффициент усиления передачи по сопротивлению. Получим в итоге линейное дифференциальное уравнение цепи с дугой в относительных единицах:

Для определения передаточных функций подвергнем обе части уравнения преобразованию Лапласа при нулевых начальных условиях:

где Y(s), F(s), Z(s) – изображения по Лапласу функций времени y(t), f(t), z(t) комплексного переменного s.

Из полученного алгебраического уравнения при Z=0 определяется передаточная функция относительно входного воздействия f(t):

Аналогичным способом при F=0 определяется передаточная функция относительно входного воздействия z(t):

Структурная схема приведена на рисунке

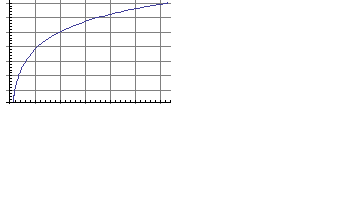
4. Построить динамические характеристики цепи с дугой: временные характеристики – переходную функцию h(t), функцию веса w(t); частотные характеристики – вещественную U(ω), мнимую V(ω), амплитудную A(ω), фазовую φ(ω), амплитудно-фазовую Y(iω), логарифмические L(lgω) и φ(lgω). В качестве входного воздействия рассматривается изменение координаты f. По графику переходной функции определить максимальное отклонение тока Δi_max от исходного значения i₀ и время переходного процесса t_п по моменту вхождения кривой процесса в зону допустимой нестабильности

Изображение переходной функции:

Используя обратное преобразование Лапласа, найдем переходную функцию:

Время переходного процесса

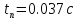
Функция веса:

Вещественная частотная характеристика:

Мнимая частотная характеристика:

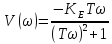
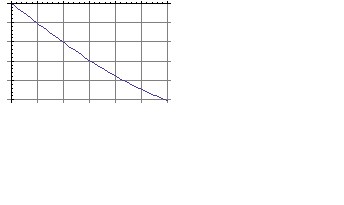
Амплитудная частотная характеристика:

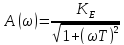
Фазовая частотная характеристика:

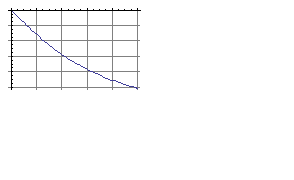
Амплитудно-фазовая частотная характеристика:

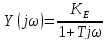
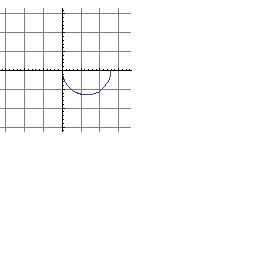
Логарифмическая амплитудная частотная характеристика

Логарифмическая фазовая частотная характеристика