лекции / Лекция 3 по ИТ для очников Переводы чисел в различные ПСС

6	Курс лекций по дисциплине «Информационные технологии» для студентов очной формы обучения
	Лекция № 3	Блок 1: «Арифметические операции в различных позиционных системах счисления над числами, представленными в алгебраической форме»
		Тема 1.3: «Методы перевода чисел из одной позиционной системы счисления в любую другую позиционную систему счисления»
	Курс – 34 акад.часа	Выпуск 1	Изменение 0	Экземпляр № 1	Лист 5/5

1.3.1 Производные двоичной системы счисления. Метод триад и тетрад для переводов из восьмеричной СС в шестнадцатеричную СС через двоичную и обратно.

Двоичная система, удобная для компьютеров, для человека неудобна из-за её громоздкости и непривычной записи.

Перевод чисел из десятичной СС в двоичную и наоборот осуществляет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы счисления.

Числа в восьмеричной и шестнадцатеричной системах счисления читаются почти также легко, как десятичные и требуют для своего представления в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем эти же числа, представленные в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

Для перевода восьмеричных и шестнадцатеричных чисел в двоичную систему счисления достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четвёркой цифр).

5 3 7 1

Например: 537,1₈ = 101 011 111, 001₂

1 А=10 3 F=15

1А3,F₁₆ = 0001 1010 0011, 1111₂

Для перевода двоичного числа в восьмеричную или шестнадцатеричную систему счисления, его нужно разбить влево и вправо от двоичной запятой на триады (для восьмеричной) и на тетрады (для шестнадуатеричной), при необходимости дописать недостающие нули и каждую такую группу заменить соответствующей восьмеричной или шестнадцатеричной цифрой.

2 5 1 5 6

Например: 10101001,10111₂ = 010 101 001, 101 110₂ = 251,56₈

А=10 9 В=11 8

10101001,10111₂ = 1010 1001, 1011 1000₂ = А9В8₁₆

1.3.2. Метод Горнера для перевода целых чисел из десятичной системы счисления в любую другую позиционную систему счисления

Для перевода целого десятичного числа N10 в систему счисления с основанием q10 необходимо число N10 разделить с остатком («нацело») на основание новой системы счисления q10, записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q10 и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа Nq в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример: Переведем число 75₁₀ в двоичную, восьмеричную и шестнадцатеричную системы счисления:

в двоичную в восьмеричную в шестнадцатеричную

7 5 2 75 8 75 16

1 37 2 3 9 8 (В₁₆ = 11₁₀) 11 4 16

1 18 2 1 8 8 4 0

0 9 2 0 1 8

1 4 2 1 0 Примечание: первый

0 2 2 11₁₀ в этом примере

0 1 2 записывается, как В₁₆

1 0

Ответ: 75₁₀ = 1001011₂ = 113₈ = 4В₁₆.

1.3.3. Метод Горнера для перевода дробной части десятичного числа в любую другую позиционную систему счисления

Для перевода дробной части F10 десятичного числа N10 в систему счисления с основанием q10 необходимо F10 умножить на основание новой системы счисления q10, записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q10 и т.д. и так до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность изображения числа F10 в q-ичной системе счисления. Представлением дробной части F10 десятичного числа N10 в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F10 составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется: Pабс

Пример 1: Переведем число 0,36₁₀ в двоичную, восьмеричную и шестнадцатеричную системы счисления:

в двоичную в восьмеричную в шестнадцатеричную

0

*

*

*

, 36 0, 36 0, 36

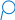2 8 16

0

*

*

*

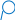72 2 88 5 76

2 8 16

1

*

*

44 7 04 (С₁₆ = 12₁₀) 12 16

Ответ: 0,36₁₀ = 0,5С₁₆

с предельной абсолютной погрешностью:

P_абс 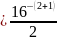= 2^–13

2 8

0

*

88 0 32

Ответ: 0,36₁₀ = 0,270₈

с предельной абсолютной погрешностью:

P_абс 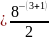= 2^–13

2

1

*

76

Ответ: 0,36₁₀ = 0,01011₂

с предельной абсолютной погрешностью:

P_абс 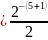= 2^–7

2

1 52

Пример 2: Переведем число 0,25₁₀ в двоичную, восьмеричную и шестнадцатеричную системы счисления:

в двоичную в восьмеричную в шестнадцатеричную

0

*

*

*

, 25 0, 25 0, 25

2 8 16

0

*

50 2 00 4 00

2

1

Ответ: 0,36₁₀ = 0,2₈

Ответ: 0,25₁₀ = 0,4₁₆

00

Ответ: 0,36₁₀ = 0,01₂

Для смешанных чисел, имеющих, как целую, так и дробную части, перевод из десятичной системы счисления в любую другую методом Горнера осуществляется отдельно для целой и дробной частей по правилам, указанным выше.

1.3.4. Метод разложения по степенному ряду для перевода из любой позиционной системы счисления в десятичную

Перевод методом разложения по степенному ряду в десятичную систему числа Aq, записанного в q-ичной системе счисления (где q = 2, 8, 16 и пр.) в виде Аq = (an–1 … a1 a0 , a–1 a–2 … a–m)q, сводится к вычислению средствами десятичной арифметики многочлена: А10 = an–1*qn–1 + …+ a1*q1 + a0*q0 + a–1*q–1 + a–2*q–2 + … + a–m*q–m, где ai – цифры исходной СС, q – основание исходной СС, n и m – количество соответственно целых и дробных разрядов исходного q-ичного числа Aq.

Например:

Разряды 4 3 2 1 0 -1 -2

Число 1 0 1 0 1 , 1 1₂=1*2⁴ + 0*2³ + 1*2² + 0*2¹ + 1*2⁰ + 1*2^-1 + 1*2^-2 = 21,75₁₀

Разряды 2 1 0 -1 -2

Число 3 0 6 , 7 1₈= 3*8² + 0*8¹ + 6*8⁰ + 7*8^-1 + 1*8^-2 = 198,890625₁₀

Разряды 2 1 0 -1 -2

Число E 1 3 , 2₁₆= 14*16² + 1*16¹ + 3*16⁰ + 2*16^-1 = 3603,125₁₀

1.3.5. Метод разложения по степенному ряду для перевода целого десятичного числа в двоичную систему счисления

Для перевода целого десятичного числа в двоичную систему счисления методом разложения по степенному ряду нужно представить исходное число в виде суммы десятичных чисел, являющихся степенями «двойки», начиная с наибольшего и двигаясь к наименьшему. Затем нужно заменить в получившемся равенстве «единицами» десятичные числа, эквивалентные степеням «двойки», а отсутствующие степени заменить нулями.

Например:

Разряды 2⁸ 2⁶ 2² 2¹ 2⁰

Число 327₁₀ = 256 + 64 + 4 + 2 + 1 = 1*2⁸ + 0*2⁷ + 1*2⁶ + 0*2⁵ + 0*2⁴ + 0*2³ + 1*2² + 1*2¹+ 1*2⁰ = 101000111₂