
3832
.pdf
копостоянства управления. Результирующий фазовый портрет и искомая оптимальная траектория, соответствующая заданным начальным условиям, представлены на рис. 5.37, в.
Рис. 5.37. Фазовый портрет системы
На первом участке
x1(t ) x2 (t ), x2(t ) u*(t ) 1
откуда
x |
(t ) t C |
, |
x (t ) |
t2 |
C |
t C |
|
|
2 |
2 . |
|||||||
2 |
1 |
|
1 |
1 |
|
При t =0 имеем x2(0)=C1= -4, x1(0)= C2=0, поэтому окончательно:
t2
x1(t ) 4t,x2(t ) t 4 2 .
Найдем время Т= 1+ 2, затрачиваемое на переход из точки x0=(0,-4)T в начало ко-
ординат. Здесь 1 – время движения с управлением u*(t)=1 до точки переключения, 2 –
время движения с управлением u*(t)=-1.
На втором участке
x1(t ) x2 (t ), |
x2(t ) u* (t ) 1 |
откуда |
|
x |
(t ) t C |
, |
x (t ) |
t2 |
C |
t C |
|
|
2 |
2 . |
|||||||
2 |
1 |
|
1 |
1 |
|
В конечный момент времени Т= 1+ 2 траектория должна попасть в начало коорди-
нат:
|
T |
2 |
|
|
|
x (T ) |
|
C T C |
|
0, |
|
|
|
2 |
|||
1 |
2 |
1 |
|
||
x2(T ) T C1 , |
|
|
|||
|
|
||||
561
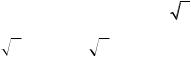
из чего следует |
C1=T= 1+ 2,Ñ |
T2 |
|
|
( |
1 |
|
2 |
)2 |
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В силу непрерывности траектории при t= 1, имеем |
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|||
|
x1( 1 ) |
1 |
4 1 |
|
1 |
( 1 |
2 ) 1 |
( 1 2 ) |
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|||||
|
x2( 1 ) 1 4 1 1 2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
. |
|||||||||||
На первом участке оптимальной траектории до линии переключения u*(t)=1, а на |
|||||||||||||||||||
втором u*(t)=-1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате получаем 2= 1-4, |
|
12-8 1+8=0 и 1 4 2 |
|
|
, так как 2 0. Поэтому |
||||||||||||||
|
|
2 |
|||||||||||||||||
2 2
 2,T 4 4
2,T 4 4
 2 9,66
2 9,66
Если модель объекта управления описывается системой дифференциальных урав-
нений
x1(t ) x2(t ) p, |
|
x2(t ) u(t ) |
|
, |
|
где p – заданное действительное число, то методика решения задачи не изменяется. Опти-
мальное управление является кусочно-постоянной функцией, имеющей не более двух ин-
тервалов знакопостоянства: на одном интервале u(t)=1, а на другом u(t)=-1. Уравнения фа-
зовых траекторий при u(t)=const:
|
|
|
dx1 |
|
x2 p |
, |
dx1 |
x2 p |
dx2 |
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dx2 |
u |
|
|
|
|
|
u |
|||||||
или, интегрируя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
px2 |
|
|
|
1 |
|
|
|
|
|
|||
x |
1 |
|
x2 |
|
C |
( x |
2 |
p)2 C |
|||||||||
|
|
|
|||||||||||||||
|
|
|
2u |
u |
|
2u |
. |
||||||||||
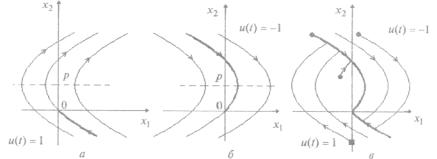
На рис. 5.38, а,б изображены соответствующие фазовые траектории, а на рис. 5.38,
в –результирующий фазовый портрет с оптимальными фазовыми траекториями.
Синтез программного управления линейными системами при
квадратичном функционале оптимизации /9/. Пусть система (5.180), опи-
сывающая поведение модели объекта управления, имеет вид (5.186), а функ-
ционал качества управления квадратичный:
|
1 t2 |
|
T |
T |
|
1 |
|
T |
|
|
|
|
|
I |
2 |
|
|
(t )S(t )x(t ) u |
|
|
(t2 |
) x(t |
,(5.191) |
||||
x |
|
(t )Q(t )u(t ) dt |
2 x |
|
2 ) |
||||||||
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
562 |
|
|
|
|
|
|
|
|
где Q(t) – неотрица- |
|
тельно определенная |
|
симметричная мат- |
|
рица размера (q q,); |
|
S(t) и – неотрица- |
|
тельно определен- |
Рис. 5.38. Фазовый портрет системы |
ные симметричные |
матрицы размера (n n). |
|
Начальное условие x(t1)=x0 Rn задано и определяет начальное состоя-
ние; на управление ограничений не наложено, т.е. u U=Rq; t T=[t1,t2] – про-
межуток времени функционирования системы, моменты начала t1 и оконча-
ния t2 процесса заданы, правый конец траектории x(t2) свободен.
Очевидно, что для достижения минимума функционала (5.191) необхо-
димо найти пару, состоящую из оптимальной траектории x*(t) и управления
u*(t).
Сравнивая (5.186), (5.191) с (5.180), (5.175), можем записать
|
|
f (t,x,u) A(t )x B(t )u, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
T |
|
|
T |
|
|
|
|
|
|
|
|
|||
|
|
L(t,x,u) |
|
|
|
S(t )x u |
|
|
, |
|
|
|
|
|||||||||
|
|
x |
|
|
Q(t )u |
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
V3 (t,x,u) |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
|
|
x . |
|
|
|
|
|
|
|
|
|
||||||||
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
( Ax ) |
|
|
( xT Ax ) |
|
|
|
|
|
|
|
|
|
BT AT , |
|
(5.192) |
||||||
|
|
AT ; |
|
|
|
|
|
Ax AT x;( AB )T |
|
|||||||||||||
|
|
|
x |
|
|
|
||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
составляем гамильтониан в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
T |
|
|
|
|
|
|
|
|
|
1 |
|
|
T |
|
|
T |
|
|
|
H(t, ,x,u) |
|
A(t )x |
B(t )u |
|
|
S(t )x u |
|
Q(t )u |
|
|||||||||||||
|
x |
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
При отсутствии ограничений на управление можно применить необхо-
димые условия безусловного экстремума для определения максимума га-
мильтониана по управлению. Тогда
563

H(t, (t ),x(t ),u) BT (t ) (t ) Q(t )u 0
u |
, |
откуда определим оптимальное управление:
u* (t ) Q 1(t )BT (t ) (t ). |
(5.193) |
Найденное управление обеспечивает максимум функции H(t, ,x,u)
по управлению, так как удовлетворяются достаточные условия максимума
2 H(t, (t ),x(t ),u)
u2
Q(t ) 0
в силу положительной определенности матрицы Q(t). Это позволяет соста-
вить систему канонических уравнений (5.184) в виде:
x(t |
) A(t )x(t ) B(t )Q 1(t )BT (t ) (t ), x(t |
1 |
) x |
0 |
|
(5.194) |
(t ) A(t ) (t ) S(t )x(t ) |
|
. |
||||
|
|
|
|
|
||
Для получения недостающих краевых условий системы (5.194), вос-
пользуемся условиями трансверсальности (5.183). Так как t2 задано, а состоя-
ние x(t2) свободно, то t2=0, а x - произвольно.
Находим вариацию функции V3 ( x ) 1 xT x :
2
.
Тогда условие трансверсальности принимает вид:
|
T |
(t2 |
) |
T |
(t2 |
T |
x 0. |
x |
|
|
) |
В силу произвольности x: (t2)= - x(t2).
Полученный результат позволяет представить двухточечную краевую задачу принципа максимума в виде
x( |
t ) A(t )x(t ) B(t )Q 1(t )BT (t ) (t ), |
x(t1 ) x0 |
|
|
||||
(t ) A(t ) (t ) S(t )x(t ), (t2 ) x(t2 ) |
|
(5.195) |
||||||
. |
||||||||
* |
|
1 |
(t )B |
T |
(t ) (t ) |
|
|
|
u (t ) Q |
|
|
|
|
|
|||
|
|
|
|
|
564 |
|
|
|
Пример 5.11. Для модели объекта x(t ) x(t ) u(t ), x(0 ) x0 при квадратичном
функционале качества управления I |
1 |
1 |
u2 |
(t ) dt |
1 |
x2 |
(1) |
min требуется найти |
|
0 |
|
||||||
2 |
|
|
2 |
|
|
|
||
оптимальную пару (x*( ), u*( )), на которой достигается минимум функционала.
Сравнивая постановку задачи с (5.186), (5.191), получаем: A(t) =-1; B(t) =1; S(t) =0;
Q(t) =1; =1; t1=0; t2 =1. Тогда система (5.195) имеет вид
|
|
|
|
|
x( |
t ) x(t ) (t ), |
|
x(t1 ) x0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
(t ) (t ), (1) x(1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
u (t ) (t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||
Решая полученную систему, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(t ) C |
et , (1) C |
e x(1), x(t ) C |
e t |
|
1 |
C |
et , x(0 ) C |
|
|
1 |
C |
|
x |
|
, |
||||||||||||||||||||||
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
2 |
2 |
|
1 |
|
0 |
|
|||
x(1) C |
e 1 |
1 |
C |
e,C |
|
|
|
2x |
0 |
|
|
,C |
|
|
|
3x |
0 |
e2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 3e2 |
|
1 3e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
2 |
1 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
а искомая пара: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x*(t ) |
x (et |
3e2 t ) |
, u*(t ) |
2x et |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 3e2 . |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 3e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
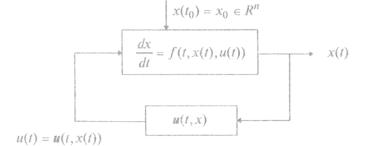
5.5.5. Синтез оптимального управления систем с полной обратной
связью
Модель объекта управления описывается уравнением (5.180) при функционале качества управления вида (5.175) /9/.
Предполагается, что при управлении используется информация о те-
кущем времени t и векторе состояния x, момент начала процесса задан, а мо-
мент окончания определяется первым моментом достижения точкой (t,x(t))
некоторой поверхности , заданной соотношениями (5.181). На множестве допустимых процессов D(t1,x(t1)=x0) задан функционал (5.175). Обозначим
Q Rn+1 множество точек (t,x), из которых можно достигнуть терминального множества по некоторой траектории, соответствующей допустимому управлению; Q(t1) – сечение множества Q при фиксированном времени t=t1.
Начальное значение x(t1)=x0 заранее не задано и может быть произвольным в
565
множестве Q(t1).
Множество Uдоп управлений с полной обратной связью (позиционных управлений) образуют функции u(t,x):T Rn U, которые для любых началь-
ных состояний порождают соответствующие тройки d=(t1,x( ),u( )) D(t1,x0),
где программные управления u( ) Uдоп, а t T u(t)=u(t,x(t)).
Применяемое в каждый момент времени t T управление имеет вид управления с полной обратной связью по вектору состояния. (рис. 5.39), при-
чем предполагается, что текущее (апостериорное) и априорное информаци-
онное обеспечение высокое.
Требуется найти такую функцию u*(t,x) Uдоп, что
I(d* ) min I(d ) |
x0 Q(t1 ), |
(5.196) |
|
d D( t1 ,x0 ) |
|
|
|
где d*=(t1* , x*( ), u*( )=u*(t,x( ))). |
|
|
|
|
Функция u*(t,x( )) Uдоп назы- |
||
|
вается |
оптимальным |
управле- |
|
нием с полной обратной свя- |
||
|
зью и |
порождает |
минимум |
|
функционала (5.175) для лю- |
||
Рис. 5.39. Система с полной обратной связью |
бого начального состояния x0 |
||
|
|
|
|
по вектору состояния |
из множества Q(t1). |
Если мо- |
|
мент окончания процесса t2 задан, оптимальное управление синтезируется в виде пары d=(x( ),u( )) D(t1,x0), порождающей минимум функционала (5.175)
для любого начального состояния x0 из множества Rn.
Достаточным условием минимума функционала (5.175) в системе с
полной обратной связью является уравнение Беллмана (Гамильтона – Якоби
– Беллмана) для непрерывных детерминированных систем /104/
V |
|
|
V |
|
0, |
(5.197) |
|
|
min |
L( x,u,t ) |
|
f ( x,u,t ) |
|||
t |
x |
||||||
u |
|
|
|
|
где
566
|
|
|
|
|
|
|
|
Vt t2 |
V3 ( x(t2 )). |
|
|
(5.198) |
||
Введем в рассмотрение множество функций (t,x):Q R, непрерывно |
||||||||||||||
дифференцируемых всюду, за исключением конечного числа сечений Q при |
||||||||||||||
фиксированных t. |
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда, если существует функция (t,x) , удовлетворяющая уравне- |
||||||||||||||
нию Беллмана с граничными условиями |
|
|
|
|||||||||||
(t,x ) |
n (t,x ) |
|
|
|
|
|||||||||
max |
|
|
|
|
|
|
|
fi |
(t,x,u) L(t,x,u) 0 |
(t,x ) Q, |
(5.199) |
|||
|
t |
|
|
|
|
|||||||||
u U |
|
|
i 1 |
xi |
|
|
|
|||||||
(t2 ,x ) V3 (t2 ,x ) |
(t2 ,x ) |
|
|
|
||||||||||
и управление, удовлетворяющее условию |
|
|
|
|||||||||||
|
|
|
n |
(t,x ) |
|
|
|
|
|
|
||||
u* (t,x ) argmax |
|
fi (t,x,u) L(t,x,u) |
u* (t,x ) Uдоп , |
(5.200) |
||||||||||
|
||||||||||||||
|
u U |
i 1 |
xi |
|
|
|
|
|
|
|
||||
то u*(t,x) является оптимальным управлением с полной обратной связью. При этом минимальное значение функционала
|
|
|
min |
I(d ) (t1 ,x0 |
) (t1 ,x0 ) Q |
|
||||
|
|
d D( t1 ,x0 ) |
|
|
|
. |
|
|||
|
|
|
|
|
|
|
||||
Если положить Б(t,x)=- (t,x), то, используя равенство max f(x)=-min[- |
||||||||||
f(x)], можно переписать (5.185) в эквивалентной форме |
|
|||||||||
|
Б |
(t,x ) |
n |
Б |
(t,x ) |
|
|
|
||
min |
|
|
|
|
|
fi |
(t,x,u) L(t,x,u) |
0, |
||
|
|
t |
|
|
|
|||||
u U |
|
i 1 |
xi |
|
(5.201) |
|||||
Б (t2 ,x ) V3 (t2 ,x )
При этом минимальное значение функционала (5.175)
min I(d ) Б (t |
1 |
,x ) |
(t |
1 |
,x |
0 |
) Q. |
d D( t1 ,x0 ) |
0 |
|
|
|
|||
|
|
|
|
|
|
|
Таким образом, отыскание оптимального управления в системе с пол-
ной обратной связью сопряжено с решением уравнения Беллмана (5.197) при граничных условиях (5.198).
Несмотря на компактную форму функционального уравнения (5.197),
его решение в практических многомерных случаях сталкивается с непреодо-
567
лимыми трудностями. Для подтверждения сказанного, положим, что v –
управление, удовлетворяющее необходимому условию локального минимума гладкой функции, находящейся в квадратных скобках уравнения (5.197). То-
гда вместо (5.197) можно записать
V |
|
|
V |
|
|
|
|
|
|||
|
|
|
|
|
f ( x,v,t ) L( x,v,t ), |
|
|||||
t |
|
|
|||||||||
|
|
t |
|
|
|
|
|
||||
|
|
|
|
|
|
V |
f ( x,v,t ) |
|
|||
L( x,v,t ) |
0 |
||||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
v |
|
|
|
|
v x |
|
|||||
|
|
|
|
. |
|||||||
Таким образом, получили систему нелинейных взаимосвязанных урав-
нений в частных производных. Только при решении этой системы уравнений с учетом условия (5.198) и последующим выражением v как функции x,t за-
дача синтеза оптимального управления в виде обратной связи может считать-
ся решенной.
В инженерных приложениях оптимальное управление с полной обрат-
ной связью можно рассматривать как временную последовательность ло-
кальных программных управлений, что позволяет использовать для синтеза принцип максимума.
Пример 5.12. Для модели объекта и минимизируемого функционала, приведенных в примере 5.11, требуется найти оптимальное управление u*(t,x) с обратной связью, пере-
водящей объект из любого начального состояния в начало координат за наименьшее вре-
мя.
В данном случае f1(t,x,u)=x2, f2(t,x,u)=u и L(t,x,u)=1, V3(t2,x) 0, x(t2)=(0 0)T.. Решает-
ся задача Лагранжа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. Для рассматриваемой задачи условие (5.199) |
имеет вид: |
|
|||||||||||||||
|
|
|
|
|
Б |
(t,x) |
|
|
Б |
(t,x) |
|
|
Б |
(t,x) |
|
|
Б(t2 ,0) 0. |
|
min |
|
|
|
x2 |
|
u 1 0, |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
u |
|
1 |
|
t |
|
x1 |
|
x2 |
|
|
||||||
|
|
|
|
|
|
||||||||||||
Так как все траектории должны попасть в точку x(t2)=(0 0)T при t= t2, то граничное условие определено только в этой точке.
2.Находим структуру оптимального управления из условия минимума выражения
вфигурных скобках
568


