Пример выполнения задания на составление рекурсивной подпрограммы
Вычислить значение определенного интеграла, если соответствующий неопределенный интеграл и первообразная функция имеют следующий вид [10]:
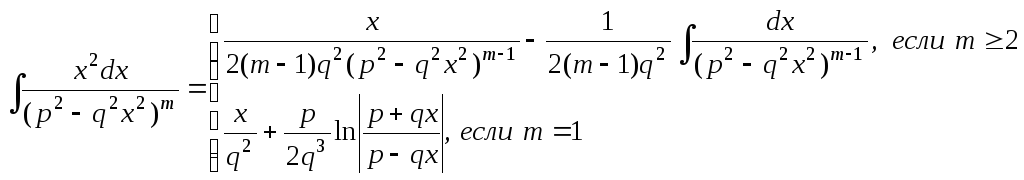
Вычисление определённого интеграла произвести двумя способами:1) с использованием приведенных выражений, вычисляемых рекурсивными подпрограммами (точное значение) и 2) с помощью численных методов (приближенно).
В основной программе необходимо осуществить ввод исходных данных – параметров p,q,m, пределов интегрированияa,bи точности ε, с которой будет вычисляться интеграл численными методами. Сравнить полученные результаты.
В рассматриваемой задаче исходный интеграл вычисляется по рекуррентной формуле, причем в этой формуле принимает участие другой интеграл, который также вычисляется по рекуррентной зависимости. Текст подпрограммы для вычисления второго интеграла необходимо в программе разместить до текста подпрограммы, в которой вычисляется исходный интеграл, так как в противном случае будет производиться обращение к еще не объявленной подпрограмме. Поскольку каждая из подпрограмм должна возвращать одно значение, то используются функции, а не процедуры.
Для приближенного вычисления интеграла использован метод парабол, причем в программе для сокращения количества выполняемых операций производится запоминание сумм значений функции, вычисленных на предыдущем шаге вычисления интеграла. Текст программы имеет следующий вид.
program PrimerRecPodp;
{$APPTYPE CONSOLE}
uses
SysUtils,Math;
var
p,q,a,b,int1,int2,eps:Real;
m,l,k:Integer;
//Рекурсивная функция вычисления второго интеграла
function Integ1(p,q:Real;m:Integer;x:Real):Real;
begin
if m>=2 then
Integ1:=x/(2*(m-1) *Power((p*p-q*q*x*x),m-1))*p*p
+(2*m-3)/(2*(m-1)*p*p)*Integ1(p,q,m-1,x)
else if m=1 then
Integ1:=Ln(Abs((p+q*x)/(p-q*x)))/(2*p*q);
end;
//Рекурсивная функция исходного интеграла
function Integ(p,q:Real;m:Integer;x:Real):Real;
begin
if m>=2 then
Integ:=x/(2*(m-1)*q*q*Power((p*p-q*q*x*x),m-1))
-1/(2*(m-1)*q*q)*Integ1(p,q,m-1,x)
else if m=1 then
Integ:=-x/(q*q)+p/(2*q*q*q)*Ln(Abs((p+q*x)/(p-q*x)));
end;
//Функция вычисления интеграла по методу парабол (Симпсона)
function SimpsonMod(a,b,eps,p,q:Real;m:Integer):Real;
var
n,i:Integer;
x,dx,sch,snch,s1,s2,i1,i2:Real;
begin
n:=Trunc((b-a)/Sqrt(Sqrt(eps)))+1;
if Odd(n) then n:=n+1;
s1:=a*a/Power((p*p-q*q*a*a),m);
s2:=b*b/Power((p*p-q*q*b*b),m);
sch:=0;
snch:=0;
dx:=(b-a)/n;
for i:=1 to n div 2 do
begin
x:=a+2*i*dx;
sch:=sch+x*x/Power((p*p-q*q*x*x),m);
x:=a+(2*i-1)*dx;
snch:=snch+x*x/Power((p*p-q*q*x*x),m);
end;
sch:=sch-s2;
i2:=(s1+s2+4*snch+2*sch)*dx/3;
repeat
i1:=i2;
n:=n*2;
dx:=(b-a)/n;
sch:=snch+sch;
snch:=0;
for i:=1 to n div 2 do
begin
x:=a+(2*i-1)*dx;
snch:=snch+x*x/Power((p*p-q*q*x*x),m);
end;
i2:=(s1+s2+4*snch+2*sch)*dx/3;
until Abs(i2-i1)/3<eps;
Result:=i2;
end;
begin// РАЗДЕЛ ОПЕРАТОРОВ ПРОГРАММЫ
Writeln('Введите значения параметровp,q,m');
ReadLn(p,q,m);
Writeln('Введите пределы интегрированияa,b'
+' и точность eps');
ReadLn(a,b,eps);
int1:=Integ(p,q,m,b)-Integ(p,q,m,a);
l:=Trunc(-Log10(eps))+2;
k:=Trunc(Log10(Abs(int1)))+m+3;
Writeln('Значение интеграла по рекурсивной функции ='
,int1:k:l);
int2:= SimpsonMod(a,b,eps,p,q,m);
Writeln('Значение интеграла по методу Симпсона ='
,int2:k:l);
ReadLn;
end.