Словесная запись алгоритмов

Пример Составим алгоритм вычисления коэффициентов приведенного квадратного уравнения x² + px + q = 0, корни которого x₁, x₂ известны.

алгоритм:

Начало.

1. Ввести x₁, x₂.

2. p = –(x₁+x₂).

3. q = x₁x₂.

4. Вывести p, q.

Конец. □

ГОСТ 19.701-90 Схемы алгоритмов , программ, данных и систем.

Схемы алгоритмов

Схема алгоритма – это графический способ его представления с элементами словесной записи.

Таблица Изображение блоков в схемах алгоритмов

Наименование символа	Обозначение и размеры	Функция
Процесс (вычислительный блок)		Выполнение операции или группы операций, в результате которых изменяются значение, форма представления или расположение данных
Решение (логический блок)		Выбор направления выполнения алгоритма в зависимости от некоторых условий
Модификация (заголовок цикла)		Выполнение операций по управлению циклом – повторением команды или группы команд алгоритма
Пуск-останов (начало-конец)		Начало или конец выполнения программы или подпрограммы
Предопределенный процесс (вызов подпрограммы)		Вызов и использование ранее созданных и отдельно описанных алгоритмов (подпрограмм)
Ввод-вывод		Общее обозначение ввода или вывода данных в алгоритме безотносительно к внешнему устройству
Соединитель		Указание прерванной связи между блокам в пределах одной страницы
Межстраничный соединитель		Указание прерванной связи между блоками, расположенными на разных листах

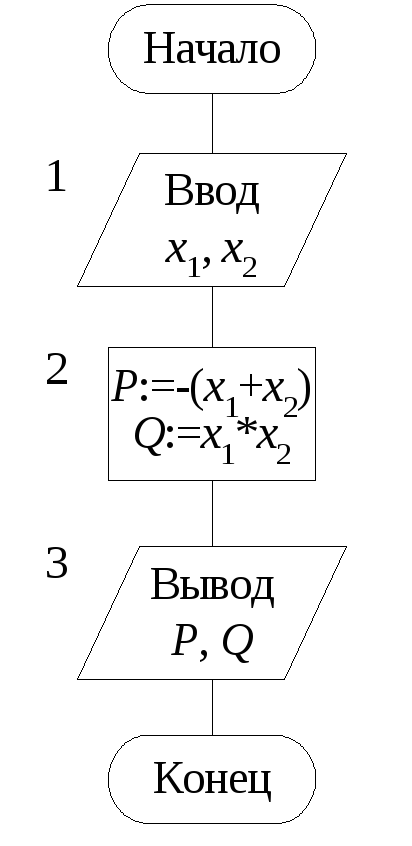
Рис. 1 Алгоритм вычисления коэффициентов приведенного квадратного уравнения

Технология разработки алгоритмов

Какими качествами должен обладать хороший алгоритм?

Прежде всего, от алгоритма требуется, чтобы он правильно решал поставленную задачу.

Но не менее важно, какой ценой это достигается. Речь идет о разумности затрат на его создание.

С этой точки зрения алгоритм должен быть легким для понимания, простым для доказательства правильности и удобным для модификации.

В рамках такой идеологии и сформировался так называемый структурный подход к конструированию и оформлению алгоритмов, позволяющий уменьшить количество ошибок в алгоритмах, упрощающий их контроль и модификацию.

По своей сути структурный подход есть отказ от беспорядочного стиля в алгоритмизации и программировании (в частности, отказ от оператора go to) и определение ограниченного числа стандартных приемов построения легко читаемых алгоритмов и программ с ясно выраженной структурой.

Теоретическим фундаментом этого подхода является теорема о структурировании, из которой следует, что алгоритм решения любой практически вычислимой задачи может быть представлен с использованием трех элементарных базисных управляющих структур:

а) структуры следования или последовательности;

б) структуры ветвления;

в) структуры цикла .

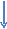
Рис.2. Базисные управляющие структуры

Базисный набор управляющих структур является функционально полным, то есть с его помощью можно создать любой сколь угодно сложный алгоритм. Однако с целью создания более компактных и наглядных алгоритмов дополнительно используются следующие управляющие структуры:

а) структура сокращенного ветвления;

б) структура выбора; в) структура цикла с параметром;

г) структура цикла с постусловием (Рис. 0 .1, соответственно а, б, в, г).

Рис. 0.1. Дополнительные управляющие структуры

Любой алгоритм может быть построен посредством композиции базисных и дополнительных структур:

- путем их последовательного соединения  образования последовательных конструкций;

- путем их вложения друг в друга  образования вложенных конструкций.

В области автоматизированной обработки данных такой подход называют нисходящим проектированием или проектированием «сверху вниз».

Разработка алгоритма по нисходящей схеме начинается с разбиения сложной исходной задачи на отдельные более простые подзадачи, решение которых может быть представлено в общей структуре алгоритма функционально независимыми блоками. Разработку логической структуры каждого такого блока и ее модификацию можно осуществлять независимо от остальных блоков.