
3263
.pdf
0 |
x2 x1 |
|
|
|
|
|
, и потому sin |
x2 |
x1 |
|
0 . Но тогда и f |
x |
f |
x |
0 , т.е. sin x возрастает на |
||||||
|
|
|
|
|
|
||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
2 |
|
|
2 |
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
отрезке |
|
|
|
; |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
При исследовании функций на монотонность бывают полезны следующие утвержде- |
||||||||||||||||||||
ния: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
Если функции |
f |
и g |
возрастают (убывают) на множестве X , то их сумма f g |
||||||||||||||||
возрастает (убывает) на этом множестве. |
|
|
|
|
|||||||||||||||||
|
б) Если функция |
f |
возрастает (убывает) на множестве |
X , то функция f возрастает |
|||||||||||||||||
(убывает) на этом множестве. |
|
|
|
|
|
|
|
||||||||||||||
|
в) Если функции |
f |
и g |
неотрицательны на множестве |
X |
и возрастают (убывают) на |
|||||||||||||||
этом множестве, то их произведение |
fg возрастает (убывает) на множестве X . |
||||||||||||||||||||
|
г) |
Если функция |
f |
положительна на множестве X |
и возрастает (убывает) на этом |
||||||||||||||||
множестве, то функция |
|
1 |
|
возрастает (убывает) на множестве X . |
|
||||||||||||||||
|
f |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
д) |
Если функция |
f |
возрастает (убывает) на множестве |
X , а функция g возрастает |
||||||||||||||||
(убывает) на множестве |
f |
X , то их композиция g f |
возрастает (убывает) на множестве X . |
||||||||||||||||||
|
Пользуясь утверждениями а) — д), легко доказать, что разность возрастающей и убы- |
||||||||||||||||||||
вающей функций возрастает, а также, что функция f |
g , где |
f |
и g положительны, f возрас- |
||||||||||||||||||
тает, а g убывает на X , является возрастающей функцией на X . Отметим еще, что прибавле-
ние к функции |
f любого числа, а также умножение функции |
f |
на любое положительное |
|||||||||||||||||||||||||||||||||||
число не изменяют характера монотонности этой функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Сформулируйте самостоятельно утверждения аналогичные а) — д) для неубывающих и |
|||||||||||||||||||||||||||||||||||||
невозрастающих функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 9. Докажем, что функция xn |
( n |
|
|
N ) возрастает на |
0, |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Решение. Функция |
xn является произведением n |
функций, |
каждая из которых равна |
||||||||||||||||||||||||||||||||||
x . Так как множители неотрицательны и возрастают на |
0, |
, |
то и функция |
xn |
( n |
N ) |
||||||||||||||||||||||||||||||||
возрастает на 0, |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 10. Докажем, что на |
|
, 0 |
|
|
функция xn ( n N ) при четном n убывает, а при |
||||||||||||||||||||||||||||||||
нечетном n возрастает. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. Если x |
x |
0 , то |
0 |
|
|
x |
|
|
|
x |
|
, и потому 0 |
x |
|
n |
|
|
x |
n . Если n |
чет- |
|||||||||||||||||
|
|
|
1 |
2 |
|
|
2 |
|
|
1 |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
||||||||||||
но, то отсюда получаем, что xn |
xn , чем доказано убывание функции xn |
на |
, 0 |
. Если же |
||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
нечетно, то получаем, что |
xn |
xn , т.е. что |
xn |
xn , |
и потому при нечетном n |
функция |
|||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
возрастает на |
, 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 11. Докажем, что функция 4 |
|
|
3x2 |
|
|
6x5 возрастает на |
0, |
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Решение. |
Данная функция является суммой числа 4 и функций 3x2 , |
6x5 , возрастаю- |
|||||||||||||||||||||||||||||||||||
щих на 0, |
, а потому она возрастает на |
0, |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Пример 12. Докажем, что функция n |
x |
( n |
|
N ) возрастает на |
|
0, |
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n , |
|
|
|
||||
|
Решение. |
Пусть 0 |
x |
x . |
Из |
n x |
|
|
|
n x |
|
|
|
следовало бы, |
что |
n x |
n x |
т.е. |
||||||||||||||||||||
|
|
|
|
1 |
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, а потому функция n |
|
|
|
|
|
|||||||||||||||||||||
x |
x вопреки предположению. Значит |
n x |
|
|
|
n x |
|
x ( n |
N ) возрастает |
|||||||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
на |
0, |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Пример 13. Докажем, что функция |
x2 |
4 возрастает на |
0, |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
f : x |
x2 |
4 и g : x |
|
|
|
||||||||||||||||||||||||||||||
|
Решение. Данная функция является композицией функций |
|
x , |
|||||||||||||||||||||||||||||||||||
причем x2 |
4 возрастает на 0, |
и принимает значения от 4 до |
|
|
, а функция g возрас- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
тает на 4, |
|
x2 |
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
. Поэтому функция |
4 возрастает на |
от |
|
4 |
|
2 до |
. |
|
|
|
|
|
||||||||||||||||||||||||||

|
|
|
|
3. Четность и нечетность |
|
|
||
|
Определение 5. Функция |
f , |
заданная на множестве |
X , называется четной, |
если |
|||
x |
X |
f |
x |
f x . |
|
|
|
|
|
Определение 6. Функция |
f , |
заданная на множестве |
X , называется нечетной, |
если |
|||
x |
X |
f |
x |
f x . |
|
|
|
|
|
Например, функция x2 четна, |
а функция x3 нечетна. Вообще, если число n Z четно, |
||||||
то и функция xn |
четна, а если число n нечетно, то и функция xn нечетна. |
|
||||||
|
Замечание. Для четных и нечетных функций область определения X должна обладать |
|||||||
следующим свойством симметричности: вместе с каждым числом x ей должно принадлежать противоположное ему число x .
Пример 14. Докажем, что функция x3 , x 4, 7 , не является ни четной, ни нечетной.
Решение. Область определения этой функции не обладает указанным выше свойством симметрии: ей принадлежит число 7, но не принадлежит число –7. Поэтому функция не является ни четной, ни нечетной.
|
При исследовании на четность или нечетность функции f , заданной своим выражени- |
|||||||||||||
ем, заменяют в этом выражении x |
на |
x |
и проверяют: а) тождественно ли получившееся вы- |
|||||||||||
ражение выражению, задающему f ; б) отличается ли оно от него лишь знаком. |
||||||||||||||
|
Пример 15. |
Докажем, что функция x4 |
5x2 |
1 четная. |
||||||||||
|
Решение. |
При |
|
замене |
x |
|
на |
|
x |
в |
выражении x4 5x2 1 получаем |
|||
f x |
x 4 5 |
x 2 |
1 |
x4 5x2 1 |
|
f |
x |
. Значит, данная функция четная. |
||||||
|
|
|
|
|
|
|
|
|||||||
|
Пример 16. |
Докажем, что функция x |
x |
нечетная. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. Имеем |
f |
x |
x |
|
x |
|
|
x |
x |
|
f x |
. Значит, данная функция нечетная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При доказательстве четности или нечетности функций бывают полезны следующие утверждения:
а) Сумма двух четных (нечетных) функций является четной (нечетной) функцией. б) Произведение двух четных или нечетных функций является четной функцией. в) Произведение четной функции на нечетную является нечетной функцией.
г) Если функция |
f |
четная, а функция g определена на |
f |
X |
, то функция g f тоже |
|
четная. |
|
|
|
|
|
|
д) Если функция |
f |
нечетная, а функция g определена на f |
X |
и является четной (не- |
||
четной), то функция g f |
четная (нечетная). |
|
|
|
|
|
Пример 17. Докажем, что любая функция вида x3 f |
x2 |
является нечетной. |
||||
Решение. Функция |
x2 четная, следовательно, и f |
x2 |
тоже четная в силу утвержде- |
|||
ния г). Поэтому данная функция является произведением нечетной функции x3 на четную f x2 , а значит, нечетна в силу утверждения в).
Теорема. Любую функцию, заданную на симметричном множестве, можно представить в виде суммы четной и нечетной функций.
Для графиков четных и нечетных функций справедливы следующие утверждения.
1.График четной функции симметричен относительно оси ординат (рис. 18).
2.График нечетной функции симметричен относительно начала координат (рис. 19).
y |
|
|
|
y |
|
|
N(-x,f(x)) |
M(x,f(x)) |
|
|
|
|
|
|
|
|
-x |
|
M(x,f(x)) |
|
-x 0 |
x |
|
|
x |
|
|
x |
N(-x,-f(x)) |
0 |
x |
|||
|
|
|
|
|
|
|

Рис. 18 |
Рис. 19 |
Справедливы и обратные утверждения:
1.Если график функции симметричен относительно оси ординат, то эта функция четна.
2.Если график функции симметричен относительно начала координат, то эта функция
нечетна.
|
|
|
4. Периодичность |
|
|
|
|
|
Определение 7. Функция f , заданная на множестве |
X , |
называется периодической с |
||||||
периодом T , если |
x |
X выполняется равенство f x |
f x |
T . |
|
|||
Число T |
0 является периодом любой функции, а вместе с T и T является периодом. |
|||||||
Поэтому достаточно рассматривать лишь положительные периоды. |
|
|||||||
Замечание. |
Из определения следует, что область определения функции f , имеющей |
|||||||
период T , сама должна обладать следующим свойством периодичности: вместе с каждым |
||||||||
числом x множества X содержит числа x |
T и x T . |
|
|
|
|
|||
Поэтому, например, функция, заданная лишь на луче 0, |
|
, не может быть периоди- |
||||||
ческой. |
|
|
|
|
|
|
|
|
Пусть T1 |
и T2 |
- периоды функции f |
. Тогда их сумма T1 |
T2 |
также является периодом |
|||
f . В частности, если T1 кратно периоду T |
для функции |
f , |
т.е. |
T1 |
nT , n Z , то T1 также |
|||
является периодом для f . Значит, периодическая функция имеет бесконечное множество пе-
риодов. Если среди положительных периодов функции есть наименьший, то его называют ос-
новным периодом этой функции. В этом случае все периоды кратны основному периоду.
|
Пусть функция |
f |
имеет основной период T . Тогда, зная значения f |
на |
0, T или |
||||||||||||||||||||
T 2 , T 2 , |
легко найти остальные значения, пользуясь периодичностью функции. Поэтому |
||||||||||||||||||||||||
при построении графика периодической функции достаточно построить этот график на |
0, T |
||||||||||||||||||||||||
или на |
T 2 , T 2 |
, а потом сдвинуть полученный график на T , |
2T , и т.д. вдоль оси |
||||||||||||||||||||||
абсцисс. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 18. Найдем основной период функции f |
x |
sin x |
sin |
|
x |
|
sin |
x |
. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
||
|
Решение. |
Так |
|
как |
основной |
период |
функции |
sin x |
равен |
2 |
, |
|
то |
имеем |
|||||||||||
f x |
sin x |
2 |
sin |
|
x |
2 |
sin |
x |
|
2 |
sin x |
2 |
sin |
x |
4 |
|
|
|
sin |
x |
6 |
. |
Таким |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|||
образом данная функция представляется в виде суммы трех функций, имеющих основные пе-
риоды T1 |
2 , |
T2 |
4 и T3 |
6 |
. Период всей функции должен быть кратен этим трем чис- |
|||||||||
лам, поэтому основной период данной функции T |
12 |
- общее наименьшее кратное перио- |
||||||||||||
дов T1 , T2 и T3 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 19. Найдем основной период функции y |
x |
, где |
x |
- дробная часть числа |
|||||||||
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Для любого |
x |
имеем |
x |
x |
1 |
x |
1 , |
так как дробные части чисел x , |
|||||
x |
1, x |
1 совпадают. Значит, |
число 1 |
– |
период функции |
x . Этот период основной, по- |
||||||||
скольку при 0 |
T |
1 равенство x T |
|
x |
не выполняется для |
x |
0 . График функции |
|||||||
y |
x изображен на рис. 20. |
|
|
|
|
|
|
|
|
|
|
|||
Рис. 20
y
1
-4 |
-3 -2 -1 0 |
1 |
2 |
3 |
4 |
x |

Пример 20. Пусть D x - функция Дирихле (см. п. 3.1). Покажем, что любое рацио-
нальное число r является периодом этой функции. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. Пусть x - иррациональное число. Тогда x |
|
|
r и x |
r тоже иррациональные |
||||||||||||||||||
числа, а потому D x |
D x |
r |
0 . Аналогично, если x |
|
- рациональное число, то и x |
r , |
||||||||||||||||
x r - рациональные числа, |
|
а потому D x |
|
|
D x |
r |
|
D x |
r |
1. Значит, при любом x |
||||||||||||
имеем D x D x r , т.е. |
r - период функции D x . Поскольку среди рациональных чисел |
|||||||||||||||||||||
нет наименьшего положительного, функция D x |
не имеет основного периода. |
|
|
|||||||||||||||||||
Пример 21. Докажем, что функция sin |
x2 не является периодической. |
|
|
|||||||||||||||||||
Решение. Решим уравнение sin x2 |
|
|
x2 |
|
|
|
|
|
0, 1, 2, 3, ) и x |
|
|
|||||||||||
0 . Имеем |
|
|
k |
( k |
k . |
|||||||||||||||||
Выпишем найденный корни: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
5, |
2, |
3, |
2, |
1, 0, 1, |
2, |
3, 2, |
5, . |
|
|
|||||||||||
Замечаем, что разности двух соседних чисел не одинаковы для различных пар чисел. Это зна-
чит, что точки пересечения графика функции sin |
x2 с осью Ox не повторяются периодиче- |
||||||||||||||||||
ски, а потому функция sin |
x2 |
не является периодической. |
|
|
|
|
|
|
|||||||||||
|
В заключение отметим, что если функция |
f задана на X и имеет период T , а функ- |
|||||||||||||||||
ция g задана на |
f |
X , то функция g f имеет тот же период. |
|
|
|
|
|||||||||||||
|
Например, |
функция |
cos x |
имеет период |
2 . Тогда тот же период имеют функции |
||||||||||||||
|
cos3 x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
5 |
cos x |
и т.д. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
3.3. Классификация функций |
|
|
|
|
|
|||||
|
Функции: |
степенная |
y |
x |
( |
R ), показательная |
y |
ax |
( a |
0 ), |
логарифмическая |
||||||||
y |
loga x |
( a |
0 , |
a |
1), тригонометрические |
y |
sin x , y |
cos x , |
y |
tg x , |
y ctg x |
и обрат- |
|||||||
ные тригонометрические функции |
y |
arcsin x , |
y |
arc cos x , |
y |
arctg x и y |
arcctg x |
называ- |
|||||||||||
ются основными элементарными функциями. Напомним основные свойства и графики этих функций.
1. Степенная функция y |
x . В общем случае она определена и непрерывна при |
||||
x 0 . При некоторых значениях |
степенная функция определена при x |
0 или при x 0 , |
|||
или и там и там. Рассмотрим различные случаи. |
|
|
|||
Пусть n |
N . Тогда при |
2n график степенной функции имеет вид, изображенный |
|||
на рис. 21, при |
2n 1 - на рис. 22, при |
2n - на рис. 23, при |
2n |
1 - на рис. 24. |
|
|
Рис. 21 |
Рис. 22 |
|
|
|
y |
|
y |
|
n |
|
|
2 |
|
|
x |
|
|
= |
|
|
y |
|
0 |
x |
0 |
1 + n 2 x = y
x

y y
y= |
1 |
y= |
2 |
1 |
x |
|
|||
x2n |
|
|
1 |
|
0 |
x |
0 |
|
x |
|
|
Рис. 23 |
|
|
Рис. 24 |
|
|
|
|
|
|
|
|
|
|||
Функция y |
x является обратной к функции y |
x , поэтому их графики симметричны от- |
||||||
носительно прямой y x (частный случай степенной функции). При |
1 |
|
график функ- |
|||||
|
|
|||||||
|
|
|||||||
|
|
|
|
|
|
2n |
1 |
|
ции имеет вид, изображенный на рис. 25, а при |
1 |
- на рис. 26 (если ограничиться ариф- |
||||||
|
|
|||||||
|
2n |
|||||||
метическими значениями корня).
y |
|
|
|
+1 |
x |
|
2n |
|
|
= |
|
|
y |
|
y |
|
n |
|
|
|
|
|
|
|
2 |
x |
|
= |
||
|
|
||
|
y |
|
|
0 |
x |
0 |
x |
|
|
|
|
Рис. 25 |
|
|
Рис. 26 |
|
|
График функции y x p q , где p, q |
Z , при p q |
1 касается оси x , а при 0 p q |
1 - |
|||
оси y . Если p q |
0 , то при неограниченном возрастании x |
значение y неограниченно убы- |
||||
вает, а при неограниченном приближении x |
к нулю y неограниченно возрастает. При x |
0 |
||||
функция y x p q |
определена не для всех |
p |
и q . Если она определена при x 0 , то является |
|||
четной или нечетной функцией, и потому ее график при |
x |
0 получается из ее графика при |
||||
x 0 с помощью той или иной симметрии. В качестве примера приведем графики функций при различных значениях p и q (рис. 27-35).
y |
|
|
|
y |
y |
|
|
|
|
|
3 |
|
|
|
|
|
/ |
|
|
|
|
|
5 |
|
|
|
3 |
|
x |
|
|
|
|
= |
|
|
|
/ |
|
y |
|
|
|
4 |
|
|
|
y |
= |
x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 / 3 x = y
0 |
x |
0 |
x |
0 |
x |
Рис. 27 |
Рис. 28 |
Рис. 29 |
y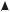
/4 3 x = y
y
|
/5 |
|
3 |
|
x |
= |
|
y |
|
y
|
/3 |
|
2 |
|
x |
= |
|
y |
|
0 |
x |
0 |
x |
0 |
x |
|
Рис. 30 |
|
|
Рис. 31 |
Рис. 32 |

y |
y |
y |
y |
|
-3 |
/4 |
|
|
|
|
|
= |
|
y |
|
-5/ |
|
|
||
|
x |
|
|
|
3 |
|
||
|
|
|
|
= |
x |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
0 |
|
|
x |
0 |
Рис. 33 |
Рис. 34 |
y=x
- |
|
2/ |
|
|
3 |
x
Рис. 35
2. Показательная функция y |
ax ( a 0 ). Она принимает положительные значения |
при всех значениях x . Если a 1, то y |
1. При x 0 показательная функция обращается в 1, |
так как a0 1 . В случае a 1 показательная функция при неограниченном убывании аргумента неограниченно приближается к нулю, а при неограниченном возрастании аргумента функция неограниченно возрастает (рис. 36). Если же 0 a 1, то показательная функция при неограниченном возрастании аргумента неограниченно приближается к нулю, а при неограниченном убывании неограниченно возрастает (рис. 37).
y
a>1
|
x |
|
|
a |
|
1 |
= |
|
y |
||
|
||
0 |
x |
y = ax
y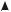
0<a<1
1
0 |
x |
|
|
|
|
Рис. 36 |
Рис. 37 |
|
|
|
|
|
|
3. |
Логарифмическая функция y |
loga x ( a 0 , a |
1). Она определена при |
x 0 . |
|||||||
Функции |
y a |
x |
и |
x loga y взаимно обратны друг другу, |
ибо y a |
loga y |
и |
loga a |
x |
x . По- |
|
|
|
|
|||||||||
этому график логарифмической функции симметричен графику показательной функции относительно прямой y x .
y |
|
|
|
|
y |
|
|
|
|
a>1 |
|
|
|
0<a<1 |
|
|
|
|
|
g x |
|
|
|
|
|
|
o a |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
y |
|
|
|
|
|
0 |
1 |
|
|
x |
0 1 |
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
a x |
|
|
|
|
|
Рис. 38 |
|
Рис. 39 |
Если |
a 1, то логарифмическая функция возрастает, причем при неограниченном воз- |
||||||
растании аргумента она неограниченно возрастает, а при неограниченном его приближении к нулю она неограниченно убывает (рис. 38). Если же 0 a 1, то логарифмическая функция возрастает, причем при неограниченном возрастании аргумента она неограниченно убывает, а при неограниченном его приближении к нулю она неограниченно возрастает (рис. 39). При
любом a |
0 , a 1, имеет место равенство loga 1 0 . |
4. |
Основные тригонометрические функции y sin x , y cos x , y tg x , y ctg x . |
Они связаны между собой соотношениями

|
sin2 x |
cos2 x 1, tg x |
sin x |
, |
ctg x |
cos x |
. |
|
|
|
|
||||||
|
|
|
|
cos x |
|
sin x |
||
Функции |
y sin x , y cos x |
определены на всей числовой оси и являются периодиче- |
||||||
скими с основным периодом T |
2 |
. При этом функция y sin x (рис. 40) является нечетной, |
||||||
а функция y |
cos x (рис. 41) является четной. |
|
|
|
|
|
||
Рис. 40
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 41 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Функция y tg x (рис. 42) не определена при x |
|
|
n , где n Z . а функция |
y |
ctg x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||
(рис. 43) не определена при x |
|
|
|
|
n , где n Z .При неограниченном приближении аргумента к |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
этим точкам значения функций неограниченно возрастают по модулю. Функции |
y |
tg x , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y ctg x являются периодическими с основным периодом T |
, а также нечетными. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 42
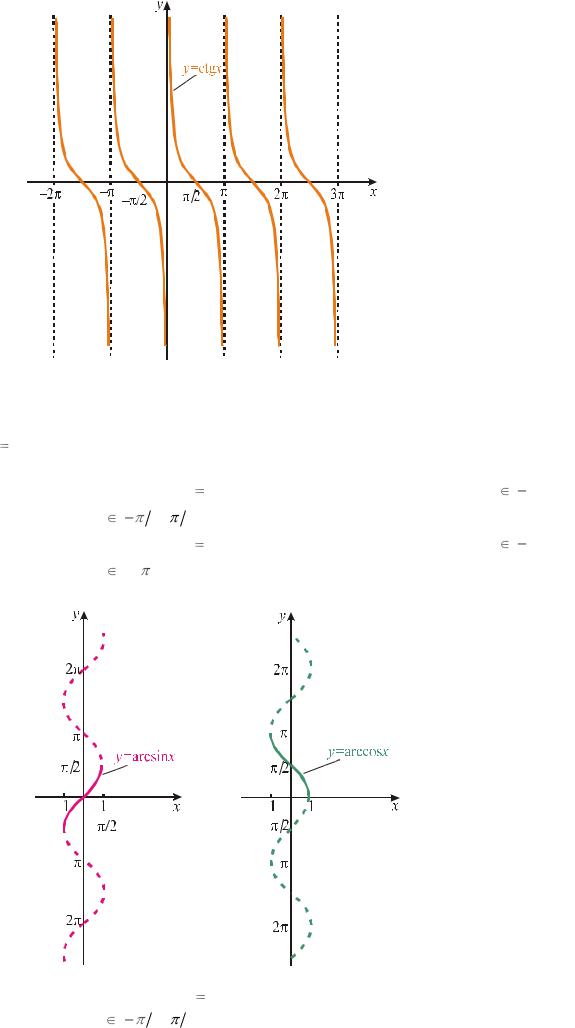
Рис. 43
5. Обратные тригонометрические функции. Так как они являются обратными для основных тригонометрических функций, то их графики симметричны относительно прямой y x графикам, изображенным на рис. 40-43. Обратные тригонометрические функции явля-
ются многозначными и обозначаются Arcsin x , Arccos x , |
Arctg x , Arcctg x . |
|
|
||||||||||||||||||
Однозначная функция y |
arcsin x (рис. 44) определена на отрезке x |
1, 1 |
и имеет об- |
||||||||||||||||||
ласть значений y |
2 , 2 . Функция монотонно возрастает и является нечетной. |
||||||||||||||||||||
Однозначная функция y |
arc cos x (рис. 45) определена на отрезке x |
1, 1 |
и имеет об- |
||||||||||||||||||
ласть значений y |
0, . Функция монотонно убывает. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 44 |
Рис. 45 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Однозначная функция |
y arctg x (рис. 46) определена на всей числовой оси и имеет об- |
|
ласть значений y |
2, |
2 . Функция монотонно возрастает и является нечетной. |

Рис. 46
Однозначная функция y arcctg x (рис. 47) определена на всей числовой оси и имеет область значений y 0, . Функция монотонно убывает.
Рис. 47
Графики соответствующих многозначных функций изображены на рис. 44-47 штриховыми линиями.
Функции, которые можно получить при помощи конечного числа арифметических операций над основными элементарными функциями, а также их суперпозицией, называются элементарными. В множестве элементарных функций выделяются следующие классы.
1. Многочлены (полиномы) – функции вида
P x an xn a1x a0 .
Если an 0 , то целое неотрицательное число n называется степенью многочлена P x .
Функция, тождественно равная нулю, является в силу данного определения многочленом, ей не приписывается никакой степени. Многочлены определены на всей числовой оси.

2. Рациональные функции – функции, представимые в виде |
f x |
P x |
, где P x |
и |
|
Q x |
|||||
|
|
|
|
||
Q x - многочлены ( Q x - ненулевой многочлен). Функция f x |
определена во всех точках |
||||
числовой оси, кроме тех точек, в которых знаменатель Q x обращается в ноль.
3. Иррациональные функции, т.е. такие функции, не являющиеся рациональными, которые могут быть заданы композицией конечного числа рациональных функций, степенных функций с рациональными показателями и четырех арифметических действий. Например,
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
функция |
f |
x |
|
3 x |
3 иррациональная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
4. Трансцендентные функции – элементарные функции, не являющиеся рациональными |
||||||||||||||||||||||||||||||||||||||||||||||
или иррациональными. Например, функция f |
x |
|
|
x sin x |
log2 2x |
3 |
|
трансцендентная. |
|
|||||||||||||||||||||||||||||||||||||||
|
Если известен график функции |
y |
f |
x , |
|
то с его помощью легко получить графики |
||||||||||||||||||||||||||||||||||||||||||
следующих функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1) график функции |
y |
|
|
f |
ax |
|
|
|
|
|
a |
0 |
получается сжатием графика f |
|
x |
вдоль оси x в |
|||||||||||||||||||||||||||||||
a раз (при a |
1) или растяжением в |
1 |
|
раз (при a |
1); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2) график функции y |
|
f |
x |
|
|
- зеркальным отображением относительно оси y ; |
|
|
|||||||||||||||||||||||||||||||||||||||
|
3) график функции |
y |
|
|
|
f |
x |
|
|
b |
|
|
- переносом параллельно оси |
x |
на |
|
b |
|
единиц вправо, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
если b |
0 , и влево, если b |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
4) график функции y |
kf |
x |
|
|
|
k |
0 |
- растяжением вдоль оси y |
в k |
раз (при k |
1) или |
||||||||||||||||||||||||||||||||||||
сжатием в |
1 |
раз (при |
k |
1); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
5) график функции y |
|
|
|
f |
x |
|
|
- зеркальным отображением относительно оси x ; |
|
|
|||||||||||||||||||||||||||||||||||||
|
6) график функции y |
|
f |
x |
|
|
l |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
- переносом параллельно оси y |
на |
l |
|
единиц вверх, если |
||||||||||||||||||||||||||||||||||||||||
l |
0 , и вниз, если l |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
7) график функции y |
|
|
f |
x |
|
|
- зеркальным отображением относительно оси x |
участков |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
графика y |
|
f |
x |
, на которых ординаты отрицательны; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
8) график функции |
y |
|
|
f |
|
x |
|
b |
|
- зеркальным отображением относительно прямой x |
b |
||||||||||||||||||||||||||||||||||||
участка графика функции y |
|
|
|
f |
x |
|
|
b |
|
при x |
b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Пример 1. Построить графики следующих функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
а) |
y |
log2 |
x |
3 |
; б) y log2 |
|
4x |
12 |
|
; в) y |
2 log2 |
x |
3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
г) |
|
|
|
; д) |
y |
log2 |
|
x |
3 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
log2 |
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
а) График функции y |
|
log2 |
|
x |
3 |
получается из графика y |
log2 x сдвигом на три еди- |
||||||||||||||||||||||||||||||||||||||||
ницы вправо (рис. 48,а). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
б) |
График |
функции |
|
|
|
y |
log2 |
|
4x |
12 |
|
log2 4 |
x |
3 |
|
получается |
сжатием |
графика |
|||||||||||||||||||||||||||||
y |
log2 |
x |
3 |
вдоль оси x |
в 4 раза (центр сжатия – прямая x |
3 ), этот график также можно |
||||||||||||||||||||||||||||||||||||||||||
получить |
сдвигом |
графика |
|
|
|
y |
log2 |
x |
3 |
|
|
на |
|
две |
единицы |
вверх, |
так |
как |
||||||||||||||||||||||||||||||
log2 4 |
x |
3 |
|
|
2 |
log2 |
x |
3 |
(рис. 48,б). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
в) График функции |
y |
|
|
2 log2 x |
|
|
3 |
получается из графика |
y |
|
log2 |
x |
3 |
растяжением |
|||||||||||||||||||||||||||||||||
вдоль оси y |
|
в два раза (рис. 48,в). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
г) При построении графика функции |
y |
|
log2 |
x |
3 |
|
участок кривой |
y |
log2 |
x |
3 , |
||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
расположенный ниже оси x , отображается симметрично относительно этой оси (рис. 48,г). |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
д) График функции |
y |
|
|
log2 |
|
x |
3 |
составляют две кривые: |
y |
log2 x 3 |
и симметрич- |
||||||||||||||||||||||||||||||||||||
ная ей относительно прямой x |
3 (рис. 48,д). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
