
3263
.pdf
7) |
x |
|
|
|
|
|
|
|
1 n |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
n |
|
|
|
sin |
|
|
|
n |
; |
|
|
|
|
|
|
8) |
|
x |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
sin2 |
|
|
|
|
|
n |
; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
1 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
9) |
x |
|
n |
1 |
|
2 |
|
1 n n |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10) |
|
x |
|
|
|
|
|
cos |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3. Вычислить пределы числовых последовательностей. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n5 |
8 |
|
|
|
|
n |
|
|
n n2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1) |
lim |
|
|
|
|
|
|
|
|
|
|
; |
|
|
2) lim |
3 |
|
|
|
n |
2 2 |
|
|
3 |
|
|
n |
1 2 |
; |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n n |
|
|
|
1 n |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
3) |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
4) |
|
lim n 3 5 |
|
|
|
8n3 |
|
|
|
|
|
2n |
; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
lim n3 |
|
|
3 n 2 n6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 n8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
5) |
|
|
|
|
4 |
|
|
|
|
|
|
|
1 |
; 6) |
|
|
lim 3 n |
3 n n |
1 |
|
|
|
|
|
; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
n2 |
5 |
|
n4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
n6 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim n |
3 5 |
|
|
|
|
n3 |
|
|
|
|
|
3 n3 |
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7) |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n n5 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n4 |
1 |
|
|
|
|
n2 |
5 |
|
|
|
|
|
||||||||||||||||||||
9) |
lim n |
|
3 4 |
|
|
|
|
n3 |
|
|
|
; |
|
|
|
|
|
10) |
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
4. Вычислить пределы числовых последовательностей. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
lim |
|
|
n2 |
|
|
|
6n 5 3n 2 |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
3n2 |
|
|
|
|
|
6n 7 |
|
|
|
|
|
n 1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|||||||||||||||||
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
5n 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
20n 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
lim |
|
|
|
4n2 |
|
|
|
4n 1 1 2n |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
2n2 |
|
|
|
|
|
2n 3 |
3n2 7 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
4n2 |
|
|
2n 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n2 |
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
7n2 |
|
|
18n 15 |
|
|
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n2 |
|
|
|
21n 7 |
|
|
|
2n 1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
5) |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
6) |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
7n2 |
|
|
11n 15 |
|
|
|
|
|
|
|
|
|
|
|
|
2n2 |
|
|
18n 9 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
lim |
|
|
|
2n2 |
|
|
7n 1 |
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
5n2 |
|
|
|
3n 1 |
|
n3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2n2 |
|
|
3n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5n2 |
|
|
|
|
|
3n 3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
lim |
|
|
|
2n2 |
|
|
5n 7 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10) lim |
|
|
|
|
|
3n2 |
|
|
|
|
|
|
4n 1 |
|
|
|
2n 5 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
2n2 |
|
|
5n 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n2 |
|
|
|
|
|
2n 7 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Группа В |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1. Вычислить пределы числовых последовательностей. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
1) |
lim |
|
|
|
2 4 |
|
2 8 2 |
2 |
2 |
; |
|
|
|
|
|
2) |
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
n n |
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3) |
lim |
|
3 n2 sin n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
|
|
lim |
1 |
|
|
|
|
|
|
3 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
2n |
1 |
|
|
|
; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
22 |
|
|
|
|
23 |
|
|
|
|
|
|
|
2n |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
5) |
lim |
|
|
|
12 |
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 2 |
|
; |
|
|
|
6) |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
2 n |
|
|
3n |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n3 |
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 n 1 |
|
|
3n 1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
7) |
lim |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
n |
|
|
|
1 |
; |
8) |
|
|
|
lim |
1 |
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n 1 n |
|
; |
||||||||||||||||||||||||||||||||||||||||||||||||||
n2 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
n |
|
|
n n n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
9) |
lim |
1 |
|
|
|
|
|
a |
|
a2 |
|
|
an |
|
a |
|
|
|
1, |
|
b |
|
1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
b |
|
|
|
b2 |
|
|
|
|
|
bn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||

10) |
lim |
|
12 |
|
|
22 |
|
|
|
n |
1 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n3 |
|
n3 |
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2. Для последовательности |
найти inf xn , |
sup xn , lim xn |
и lim xn . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) x |
|
|
1 |
|
; |
|
|
|
2) x |
|
|
n 2 |
1 n ; |
3) |
x |
|
1 n n ; |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
n |
|
n |
10,5 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
x |
1 |
nsin |
n |
|
; |
5) |
x |
n |
|
|
1 n |
; |
6) x |
|
n |
1 |
cos |
2n |
|
|
; |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
n |
|
|
|
|
|
2 |
|
|
|
|
n |
|
|
|
|
|
n |
|
n |
1 |
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 2 1 n 1 |
|
|
n n 1 |
|
|
|
|
|
|
1 n 1 2 |
3 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
; |
|
|
|
||||||||||||||||||||||
7) |
x |
3 1 n ; |
8) x |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9) |
x |
|
|
|
|
1 n |
1 |
|
|
1 n |
; |
10) |
x |
1 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
|
n |
|
|
|
|
|
2 |
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3. Выполнить следующие задания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1) |
Доказать, что последовательности xn |
|
и |
yn |
, определяемые формулами |
||||||||||||||||||||||||||
|
|
b , |
|
|
|
|
|
|
|
, y |
|
xn |
yn |
|
имеют общий предел |
|
|
lim y . |
|
|
|
|
|
||||||||||
y |
|
x |
|
|
|
|
x y |
n 1 |
lim x |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
|
|
|
|
n 1 |
|
|
|
|
n |
n |
|
2 |
|
|
|
|
|
|
|
|
n |
n |
|
n |
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2) Пусть |
xn |
- последовательность чисел, определяемая следующей формулой |
||||||||||||||||||||||||||||
x |
|
1 |
|
x |
1 |
|
, |
n |
0, 1, 2, . Доказать, что |
lim x |
|
1. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
n 1 |
2 |
|
n |
|
xn |
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
3) |
Доказать, |
что |
последовательность |
|
xn |
, |
где |
|
xn |
|
1 |
1 |
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
3 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n1, 2, , сходится.
4)Доказать, что если p - натуральное число, то
x1 a ,
x0 0 ,
1 |
ln n |
|
|
||
n |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
1p |
|
2 p |
n p |
n |
1 |
. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n p |
|
|
|
p 1 |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
5) |
|
Доказать, |
что если |
|
y |
n 1 |
|
y |
n |
, |
|
lim y |
|
|
и |
существует |
lim |
xn 1 |
xn |
, |
то |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
n |
yn 1 |
yn |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
xn |
|
lim |
xn 1 |
xn |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n |
|
yn |
n |
|
yn 1 |
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
6) Доказать, что lim |
n |
e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
n n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
xn 1 |
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
7) Доказать, что если |
x |
n |
0 , то |
lim |
n x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
n |
xn |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
8) |
|
Доказать, |
что |
|
если |
|
|
последовательность |
xn |
сходится |
и |
xn |
0 , |
то |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim n x x x |
|
|
lim x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n |
|
1 |
2 |
n |
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
9) Доказать, что если |
lim xn |
|
|
|
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x1 |
|
x2 |
|
xn |
|
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
10) |
|
Пусть |
|
числовая |
|
|
последовательность |
xn |
удовлетворяет |
условию |
||||||||||||||||||||||||||
0 |
x |
|
x |
|
x |
. Доказать, что |
lim |
xn |
существует. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
m n |
|
m |
|
n |
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

3. ДЕЙСТВИТЕЛЬНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
3.1. Определение числовой функции
Определение 1. Пусть X и Y – произвольные множества действительных чисел. Если
на множестве X задано отображение |
f , при котором каждому x |
X соответствует действи- |
||||||||||||||||||
тельное число y Y , то говорят, что на множестве |
X |
определена действительная функция |
||||||||||||||||||
y f x |
действительной переменной x . Множество X |
называется областью определения, а |
||||||||||||||||||
множество Y - множеством значений числовой функции f x . |
|
|
|
|
|
|||||||||||||||
Определим арифметические операции над функциями. |
|
|
|
|
|
|||||||||||||||
Определение 2. Пусть функции |
f и g определены на множестве X R . Суммой f |
g |
||||||||||||||||||
называют функцию, значение которой для каждого x |
|
|
X равно сумме значений функций f |
и |
||||||||||||||||
g для этого значения x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
f |
g |
|
x |
f |
x |
|
|
g |
x . |
|
|
|
|
|
|||
Аналогично вводится понятие разности функций: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
f |
g |
|
x |
f |
x |
|
|
|
g |
x . |
|
|
|
|
|
||
Произведением функций f и g называют такую функцию fg на множестве X , что |
|
|||||||||||||||||||
|
|
|
fg |
x |
f |
x |
g |
|
|
x . |
|
|
|
|
|
|||||
Если функция g задана на множестве |
X |
|
и не обращается на нем в нуль, то через |
1 |
обозна- |
|||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
чают такую функцию на X , что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
x |
|
1 |
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
g |
|
|
|
g |
x |
|
|
|
|
|
|
||||
Функцию |
f |
1 |
называют частным функций |
f и |
g и обозначают |
f |
. Таким образом, |
|
||||||||||||
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
||||
|
|
|
|
|
f |
|
|
x |
f |
x |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
g |
|
|
g |
x |
|
|
|
|
|
|
|||||
Понятия суммы, разности, произведения и частного функций применяют и в том случае, когда данные функции имеют различную область определения. В этом случае их рассматривают на пересечении областей определения.
Пример 1. Пусть функция |
f ставит в соответствие каждому числу x из |
отрезка |
||
4, 7 число x2 |
1, а функция g ставит в соответствие каждому числу x из отрезка |
2, 10 |
||
число x3 . Найдем сумму этих функций. |
|
|
||
Решение. Имеем 4, 7 |
2, 10 |
2, 7 . Функция f g ставит в соответствие каж- |
||
дому числу x |
2, 7 число x2 1 |
x3 . |
|
|
Задать функцию - значит указать закон, по которому каждому значению аргумента из области определения ставится в соответствие значение зависимой переменной из области значений функции.
Наиболее часто используются три способа задания функции: аналитический, табличный и графический. Аналитический состоит в том, что с помощью формулы устанавливается алгоритм вычисления значения функции для каждого из значений аргумента x , областью определения функции в этом случае считается множество значений аргумента, при которых данная формула имеет смысл.
Пример 2. Найти область определения функции
1 |
|
|
1 |
|
|
|
|
|
|
|
|
f x |
3x 6 |
|
7x |
56 |
. |
|
|
|
|
||
|
x2 |
3x |
2 |
|
|

Решение. Это выражение имеет числовое |
значение, если |
3x 6 0 , 7x 56 0 и |
||||
x2 3x 2 0 . Иными словами, |
для нахождения области определения надо исключить из R |
|||||
корни уравнений 3x 6 0 , |
7x |
56 |
0 и x2 |
3x 2 |
0 . Решая эти уравнения, получаем кор- |
|
ни: -2, 8, 1, 2 и записываем область определения данной функции |
|
|||||
x |
, 2 2, 1 1, 2 2, 8 8, |
. |
||||
В некоторых случаях функция задается на различных числовых множествах разными |
||||||
выражениями, например |
|
|
|
|
|
|
|
|
|
x, |
если x |
0, |
|
|
|
f |
x |
|
|
|
|
|
|
x2 |
1, если x 0, |
|
|
или (функция Дирихле) |
|
|
|
|
|
|
f |
x |
1, если x |
рациональное число, |
|
||
|
|
|
|
|
||
0, если x иррациональное число.
На практике часто удобным оказывается табличный способ задания функций, например, при экспериментальных измерениях, социологических опросах, при составлении отчетов банковской деятельности и т.д. На табличном способе задания, хранения и обработки информации основаны базы данных. В общем случае таблица имеет вид
x1 |
x2 |
x3 |
|
xn |
f x1 |
f x2 |
f x3 |
|
f xn |
Она позволяет находить значения функции для выбранных значений аргумента. Таким образом, таблица не задает функции, поскольку для задания функции надо знать ее значения для всех x X , а не только для некоторых. Существуют методы, позволяющие по такой таблице
подбирать выражение f x , разумеется, с определенной точностью.
При графическом способе соответствие между аргументом и функцией задается посредством графика.
Определение 3. Графиком функции y |
f x называется множество пар |
x, y R R : x X , y f x . |
|
Каждая пара x, y состоит из двух чисел, |
а потому может быть изображена точкой M x, y |
на координатной плоскости. Следовательно, график числовой функции может быть наглядно изображен множеством точек координатной плоскости. Это множество также принято назы-
вать графиком данной функции:
M x, y : x X , y f x .
Обычно графиком функции является некоторая линия. Однако, не всякое множество точек плоскости является графиком некоторой функции. Из определения функции следует, что
каждому значению x X соответствует только одно значение f x , а потому прямая, парал-
лельная оси ординат, может пересекать график функции не более чем в одной точке. Например, окружность не является графиком какой-либо функции, так как прямые, параллельные оси ординат, могут пересекать ее в двух точках; полуокружность на рис. 8, а является графи-
ком функции R2 x2 , а полуокружность на рис. 8, б – графиком функции |
R2 x2 . |
|
y |
|
y |
|
|
|
-R |
|
R |
-R |
0 |
R x |
0 |
x |
|
а) |
|
б) |
|
|
|
|
Рис. 8 |
|
На практике строят не графики функций, а эскизы таких графиков. Для этого обычно составляют таблицу значений функции для некоторых значений аргумента, наносят на плоскость соответствующие точки и соединяют их линией. При этом предполагается, что график функции является достаточно плавной линией, а найденные точки достаточно точно показывают ход изменения функции. Если эти предположения не выполняются, то построенный график будет сильно отличаться от истинного.
Пример 3. Построим график функции |
|
1 |
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
0,5 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
x |
0,1 |
|
|
|
||||
Решение. Составляем таблицу значений функции для x |
3, 4 |
с шагом 1. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
-3 |
-2 |
-1 |
|
0 |
|
1 |
|
2 |
3 |
4 |
|
|
|
f x |
0,10 |
0,16 |
0,42 |
|
2,86 |
|
2,86 |
|
0,42 |
0,16 |
0,10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наносим полученные точки на плоскость и соединяем их плавной непрерывной линией. Получаем график, изображенный на рис. 9, а. Заметим, что этот график значительно отличается от истинного (рис. 9, б) в связи с большим значением шага таблицы.
y
10
8
y
6
4 |
4 |
|
|
3 |
|
|
|
2 |
2 |
|
|
1 |
|
|
|
-3 -2 -1 0 1 2 3 4 x |
-3 -2 -1 0 1 2 3 4 x |
||
а) |
|
б) |
|
|
|
Рис. 9 |
|
Не всякий график изображается непрерывной линией, например график функции |
|||
|
|
1, если x |
0, |
|
y sign x |
0, если x |
0, |
|
|
1, если x |
0 |
имеет один разрыв (рис. 10), а график функции y x |
- целая часть числа x - имеет беско- |
||
нечное число разрывов (рис. 11). |
|
|
|

y |
|
|
y |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
1 2 3 x |
|
|
|
|
||
0 |
x |
-2 -1 0 |
|
||
|
|
|
|
-1 |
|
|
-1 |
|
|
|
-2 |
|
|
|
|
|
|
|
|
Рис. 10 |
|
|
Рис. 11 |
Встречаются функции, графики которых невозможно изобразить. Примером такой функции является функция Дирихле, определенная выше. Так как на сколь угодно малом отрезке числовой прямой имеются как рациональные, так и иррациональные точки, то график функции Дирихле не является линией. Он состоит из точек оси абсцисс с иррациональными абсциссами и точек прямой y 1 с рациональными абсциссами. Построить такой график не-
возможно. |
|
|
|
Пусть известны графики заданных на |
X |
функций f и g . |
Чтобы построить график |
функции f g , достаточно для каждого x |
X |
сложить ординаты графиков этих функций. |
|
Чтобы построить график функции f g , достаточно для каждого x |
X перемножить ордина- |
||
ты графиков функций f и g . При этом f g |
обращается в нуль, если хотя бы одна из функ- |
||
ций f , g обращается в нуль в данной точке. График функции a f |
строят, деля a на ордина- |
||
ты графика функции f . При этом в точках, где |
f обращается в нуль, функция a f не опре- |
||
делена. Обычно около этих точек график функции a f неограниченно удаляется от оси абсцисс.
f неограниченно удаляется от оси абсцисс.
|
6x |
|
Пример 4. Построим график функции y |
|
. |
1 x2 |
||
Решение. Строим график функции x2 . Прибавляя к ординатам этого графика 1, получаем график функции 1 x2 . Выполняя деление числа 6 на ординаты последнего графика, по-
6
лучаем ординаты графика функции 1 x2 . Перемножая найденные ординаты и ординаты гра-
фика функции x , получаем искомый график. На рис. 12 изображено последовательное по-
строение графика функции y |
6x |
|
|
. |
|
1 x2 |
||
y
y=
6 1+x2
7
6
5
4
3
2
1
2 |
|
x |
|
+ |
|
1 |
|
= |
2 |
y |
x |
|
= |
|
y |
|
x |
= |
|
y |
|
y=
-5 -4 |
-3 |
-2 -1 0 |
1 |
2 3 4 |
5 x |
||||
6x |
|
|
|
-1 |
|
|
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
||||||
1+x |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
-3 |
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 12
На практике применяются приборы, автоматически записывающие ход изменения некоторых величин с течением времени (осциллографы, термографы, сейсмографы и т.д.). Они задают графики этих величин как функции времени. Следует иметь в виду, однако, что это задание является лишь приближенным, так как получающаяся линия имеет некоторую толщину, и

потому значение |
y , соответствующее данному значению t , определяется по графику лишь |
||||||||||||||||||||||||||||||||
приближенно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Определение 4. Пусть числовая функция |
f |
x задана на множестве |
X , |
а функция |
|||||||||||||||||||||||||||
g |
y |
- на множестве Y , и пусть |
f x |
|
Y . Тогда существует отображение g f |
множества |
|||||||||||||||||||||||||||
X |
в |
R , |
задаваемое формулой |
g f |
|
x |
|
g |
f |
x |
. Это отображение является числовой |
||||||||||||||||||||||
функцией, заданной на множестве X , и называется суперпозицией (композицией) функций или |
|||||||||||||||||||||||||||||||||
сложной функцией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Для математического анализа наиболее существенным является случай, когда функции |
|||||||||||||||||||||||||||||||
f |
и g заданы своими выражениями f |
x |
и g |
x |
. В этом случае выражение функции g f |
||||||||||||||||||||||||||||
получается следующим образом: в выражении |
g |
x |
каждое вхождение буквы |
x |
заменяется |
||||||||||||||||||||||||||||
выражением |
|
f |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Пример 5. Найдем выражение для суперпозиций |
g f и |
f g , |
где |
f |
x |
x3 |
1 , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
x |
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
каждое вхождение буквы x на x3 |
1 , полу- |
|||||||||||||||||||
|
|
Решение. Заменяя в выражении |
|
x |
3 |
|
x |
||||||||||||||||||||||||||
чаем выражение |
|
x3 |
4 |
|
x3 |
1 для функции g f . Таким же образом получаем выражение |
|||||||||||||||||||||||||||
|
|
|
|
x 3 |
|
|
|
|
f g . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
3 |
|
|
1 для функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Может случиться, что множество значений выражения, задающего функцию |
f , не яв- |
||||||||||||||||||||||||||||||
ляется подмножеством области определения Y функции |
g . Тогда выражение, полученное |
||||||||||||||||||||||||||||||||
подстановкой выражения для |
f в выражение для g , определяет функцию g f |
лишь для тех |
|||||||||||||||||||||||||||||||
x , при которых f |
|
x |
Y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пример 6. Найдем область определения функции g f , если g x |
|
|
|
f |
x |
4 |
x2 . |
||||||||||||||||||||||||
|
|
|
x , |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Решение. Так как |
|
x |
имеет значение лишь при x |
0 , то искомая область определения |
|||||||||||||||||||||||||||
функции g f |
задается неравенством 4 |
|
x2 |
|
0 . Из него находим, что x |
2, 2 . |
|
|
|
||||||||||||||||||||||||
|
|
Определение 5. Функция, определенная на множестве Y значений функции |
f , с обла- |
||||||||||||||||||||||||||||||
стью значений, принадлежащей множеству |
X , и ставящая в соответствие каждому элементу |
||||||||||||||||||||||||||||||||
y |
Y |
его прообраз x : |
f |
x |
y , называется обратной к |
f функцией и обозначается через |
|||||||||||||||||||||||||||
f |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратная функция является, вообще говоря, многозначной функцией. Если отображе- |
|||||||||||||||||||||||||||||||
ние f : X |
|
Y |
является взаимно однозначным (см. п. 1.2), то обратная функция является од- |
||||||||||||||||||||||||||||||
нозначной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Обратная функция также является числовой функцией. Если известно выражение |
|||||||||||||||||||||||||||||||
функции |
|
f |
, |
|
то |
выражение |
для |
f 1 |
получают следующим образом. Пишут |
уравнение |
|||||||||||||||||||||||
y |
f |
x |
и решают его относительно x . При этом могут получиться несколько выражений. Из |
||||||||||||||||||||||||||||||
них надо выбрать то, значения которого принадлежат множеству |
X . Получают равенство |
||||||||||||||||||||||||||||||||
x |
f |
1 |
y |
. Тогда |
|
f 1 |
y |
и будет выражением обратной функции. Обычно в этом выражении |
|||||||||||||||||||||||||
заменяют |
y |
|
на x . Выражение обратной функции не всегда можно записать с помощью из- |
||||||||||||||||||||||||||||||
вестных нам функций. Поэтому операция образования обратной функции может привести к расширению запаса функций.
|
|
Пример 7. Найдем обратную функцию для функции x2 |
|
4 , x |
0 . |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
Решение. |
Из уравнения y |
4 находим |
x |
|
y |
4 или |
x |
|
y 4 . Значениям |
||||||||||
x |
0, |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
соответствуют значения |
|
y |
4 , где y |
4 . Поэтому обратная функция задается |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
выражением |
|
|
y |
4 и определена на луче 4, |
. |
Если заменить y |
на x , то получим |
||||||||||||||
|
1 x |
|
|
|
|
|
|||||||||||||||
f |
|
x |
4 , |
x 4 . Графики прямой и обратной функции изображены на рис. 13. |
|||||||||||||||||

Замечание. Если точка M x, y принадлежит графику функции f , то точка N y, x
принадлежит графику функции f 1 , и обратно, из принадлежности точки N y, x графику функции f 1 следует принадлежность точки M x, y графику функции f . Но точки M x, y
y
7
6
5
4
3
2
1
|
x |
= |
|
y |
|
|
4 |
|
|
y= |
x+ |
|
|
-5 -4 -3 -2 -1-1 |
0 |
1 2 3 4 5 6 7 8 |
x |
||
|
|
|||||
|
|
|
4 |
|
||
|
|
|
|
|
|
|
|
-2 |
|
|
|
2- |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
-3 |
|
|
y |
|
|
|
|
|
|
|||
|
-4 |
|
|
|
|
|
|
|
|
|
|
||
и N |
y, x симметричны относительно прямой y x . Значит, графики функций f и f 1 сим- |
|||||
метричны друг другу относительно прямой y x . |
|
|||||
|
|
|
|
|
Рис. 13 |
|
|
На рис. 13 изображены графики взаимно обратных функций и показана их симметрия |
|||||
относительно прямой y x . |
|
|
||||
|
В заключение приведем теорему, используемую при нахождении обратных функций. |
|||||
|
Теорема. Пусть функция f непрерывна и возрастает (убывает) на промежутке X и |
|||||
f X |
Y . Тогда существует заданная на Y обратная к f функция f 1 , причем эта функция |
|||||
возрастает (убывает) и непрерывна на Y . |
|
|||||
3.2.Свойства функций
1.Ограниченность.
Определение 1. Функция f , заданная на множестве X , называется ограниченной сверху (снизу) на этом множестве, если существует такое число M , что для всех x X выполняет-
ся неравенство |
f x |
|
M ( f |
x |
M ): |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
M R x X f x M f x M . |
||||||||||||||||
|
|
Определение 2. Функция |
f |
называется ограниченной на множестве X , если сущест- |
||||||||||||||||||||
вует такое M |
0 , что |
|
f x |
|
|
M для всех x |
X : |
|||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
M |
0 |
|
|
x |
X |
|
f x |
|
M . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пример 1. Докажем, что функция |
|
|
x2 |
|
ограничена. |
|||||||||||||||||
|
|
1 |
|
x2 |
||||||||||||||||||||
|
|
Решение. Так как |
|
x2 |
|
1 |
|
|
1 |
|
|
, |
то для любого x R выполняются неравенства |
|||||||||||
|
|
1 |
x2 |
|
1 x2 |
|||||||||||||||||||
0 |
|
x2 |
1. Значит функция |
|
x2 |
|
ограничена на R . |
|||||||||||||||||
|
x2 |
|
|
|
x2 |
|||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При доказательстве ограниченности функций оказываются полезными следующие утверждения:

|
|
|
|
а) Если функция |
|
f |
ограничена на множествах X1 |
и X2 , то она ограничена и на объе- |
|||||||||||||||||||||||||||||||||||||||||||||||
динении X |
|
X1 X 2 |
|
этих множеств. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
б) Если функции |
|
f |
и g ограничены на множестве X , то их сумма f |
g |
и произведе- |
||||||||||||||||||||||||||||||||||||||||||||||
ние |
|
fg ограничены на X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
в) Если функция |
|
f |
ограничена на множестве X |
сверху, то |
f |
ограничена на X сни- |
|||||||||||||||||||||||||||||||||||||||||||||
зу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
Если функция |
|
f |
|
положительна на |
|
X и ограничена на X |
снизу положительным |
|||||||||||||||||||||||||||||||||||||||||||
числом, то функция 1 f |
ограничена на X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
Пример 2. Докажем, |
что функции x3 |
|
5x2 |
|
x |
3 и |
|
|
1 |
|
|
ограничены на от- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
x3 5x2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
||||
резке 0, 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Решение. Функция x ограничена на |
0, 1 , так как на этом отрезке выполняется нера- |
||||||||||||||||||||||||||||||||||||||||||||||||||
венство 0 |
|
x 1. Постоянные функции |
f |
|
x |
|
|
5 и |
g |
x |
3 также ограничены на |
0, 1 . За- |
|||||||||||||||||||||||||||||||||||||||||||
данную |
функцию |
|
можно |
представить |
как |
|
сумму произведений ограниченных функций: |
||||||||||||||||||||||||||||||||||||||||||||||||
x3 |
|
5x2 |
x |
3 |
x |
x |
x |
5 x |
x |
x |
3 , |
а |
тогда |
по |
утверждению |
б) |
функция |
ограничена на |
|||||||||||||||||||||||||||||||||||||
0, 1 . Так как значения функции x3 |
5x2 |
|
x |
|
3 на |
0, 1 не меньше, чем 3, и она ограничена, |
|||||||||||||||||||||||||||||||||||||||||||||||||
то по утверждению г) функция |
|
|
|
|
|
1 |
|
|
|
|
|
|
ограничена на |
0, 1 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
x3 |
5x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
Сформулируем теперь отрицания введенных понятий. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
Определение 3. Функция f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
- неограничена сверху на X : |
M |
x |
X |
|
|
|
f |
|
x |
|
|
|
M |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
- неограничена снизу на X : |
M |
|
|
x |
X |
|
|
f |
x |
|
M |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
- неограничена на X : |
|
|
M |
|
x |
X |
|
f |
|
x |
|
|
|
M . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
Пример 3. Докажем, что функция |
|
f |
|
x |
|
|
|
1 |
|
не является ограниченной на |
0, 1 . |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Решение. Возьмем произвольное M |
|
0 и докажем, |
что существует x |
|
0, 1 |
|
, такое, |
||||||||||||||||||||||||||||||||||||||||||||
что |
|
|
|
|
M |
, т.е. |
|
1 |
|
|
|
M . Это и будет означать неограниченность функции |
1 |
|
на |
0, 1 |
. Возь- |
||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
x |
|
|
|
x |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
мем x |
|
1 |
|
. Тогда |
1 |
|
|
|
1 |
|
|
|
2M |
M . Неограниченность функции доказана. Заметим, что |
|||||||||||||||||||||||||||||||||||||||||
2M |
|
x |
1 (2M ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
на любом интервале |
|
, 1 , где |
|
|
0 , эта функция ограничена: если 0 |
|
|
x , то |
1 |
|
1 |
. |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4. Докажем, что функция |
|
f |
|
x |
|
|
|
x cos 2 |
x , |
|
|
x |
|
, не ограничена. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. |
|
При x |
n , n |
|
N , имеем |
f |
n |
n cos 2 |
n |
n , |
и потому f |
x |
принимает |
||||||||||||||||||||||||||||||||||||||
сколь угодно большие значения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
Если функция |
|
f |
ограничена на множестве |
X , то множество ее значений на |
X имеет |
||||||||||||||||||||||||||||||||||||||||||||||
точную верхнюю и точную нижнюю грани. Их обозначают sup f |
x |
|
и inf f |
x |
. Индекс X |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
X |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обычно опускают. Числа sup f |
x |
и inf f |
x |
|
могут как принадлежать, так и не принадлежать |
||||||||||||||||||||||||||||||||||||||||||||||||||
множеству значений функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
Пример 5. Для функции |
|
f |
x |
|
sin x , |
|
x |
|
R , |
имеем sup f |
x |
1, inf f |
x |
|
|
1 . Значе- |
|||||||||||||||||||||||||||||||||||
ния 1 и –1 принадлежат множеству значений функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
Пример 6. Для функции |
f |
x |
|
|
x2 |
|
, |
x |
R , имеем sup f |
x |
|
1 , inf f |
x |
|
0 . Значе- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x2 |
|
4 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ние 0 функция принимает при x |
0 . Значение 1 эта функция не принимает ни при каком x . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Но |
среди значений |
функции есть сколь угодно близкие к 1. Так, при |
x |
1000 |
имеем |
||||||||||||||||||||||||||||||||||||||||||||||||||
f 1000 |
|
|
10002 |
|
|
|
1 |
|
|
|
4 |
|
|
|
. Это значение отличается от 1 меньше чем на 0,000004. |
||||||||||||||||||||||||||||||||||||||||
10002 |
4 |
|
|
|
1000004 |
||||||||||||||||||||||||||||||||||||||||||||||||||
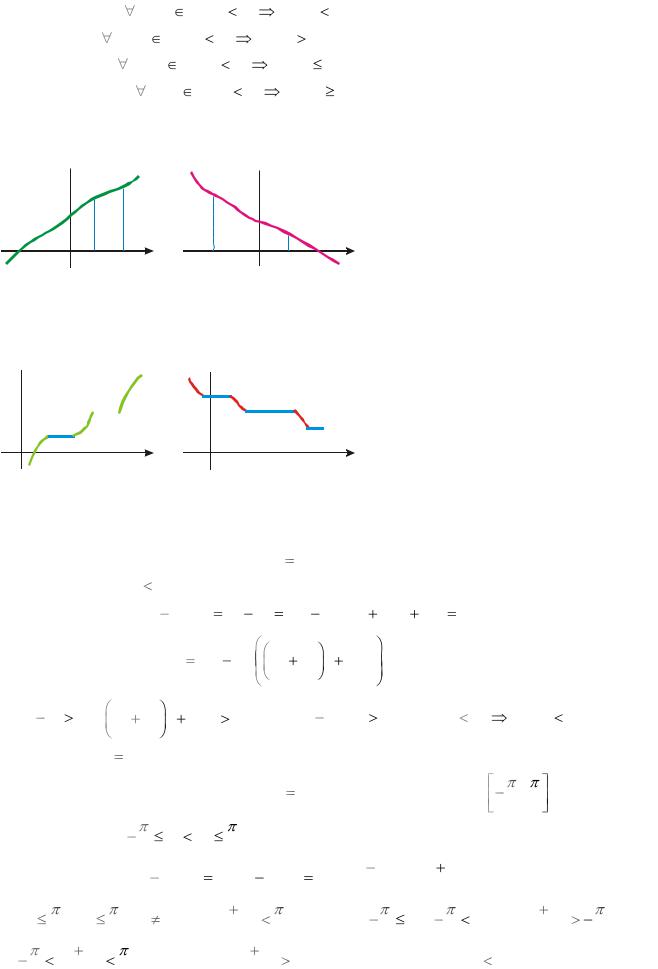
|
|
|
2. Монотонность |
|
|||||
Определение 4. |
Функция f |
называется: |
|
|
|
|
|||
- возрастающей на X : |
x1, x2 |
X |
x1 |
x2 |
f |
x1 |
f |
x2 ; |
|
- убывающей на X : x1, x2 X |
x1 |
x2 |
f |
x1 |
f |
x2 |
; |
||
- неубывающей на X : |
x1, x2 |
X |
x1 |
x2 |
f x1 |
f |
x2 |
; |
|
- невозрастающей на X : x1, x2 |
X x1 |
x2 |
f |
x1 |
|
f |
x2 . |
||
При движении вдоль оси абсцисс слева направо ордината графика возрастающей функции увеличивается (рис. 14), а ордината графика убывающей функции уменьшается (рис. 15).
y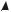
|
|
|
) |
|
|
x |
|
|
( |
|
|
|
f |
|
|
= |
|
|
|
y |
|
|
|
y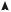
y=f(x)
0 x1 x2 x |
x1 |
0 |
x2 |
x |
|
Рис. 14 |
|
|
Рис. 15 |
Графики неубывающей функции (рис. 16) и невозрастающей функции (рис. 17) могут иметь «площадки».
y
0
|
|
(x |
) |
|
|
|
|
||
y |
= |
f |
|
|
|
|
|
||
|
|
|
|
|
y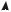
x 0
Рис. 16
y = f ( x )
 x
x
Рис. 17
Если функция возрастает (убывает, не возрастает, |
не убывает) на |
X , |
то говорят, что |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
она монотонна на X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример 7. Докажем, что функция |
f |
x |
x3 |
возрастает на всей числовой прямой. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. Пусть x1 |
|
x2 . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
f x |
f x |
|
|
x3 |
|
x3 |
x |
x x2 |
|
x x |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
2 |
|
1 |
|
|
|
2 |
1 |
2 |
1 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
x |
|
|
|
x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
2 |
2 |
|
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как x |
x |
0 и |
x |
|
|
|
|
x2 |
|
0, то f |
x |
f |
x |
|
0. Итак, |
x |
x |
|
|
f x |
|
f x . |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
2 |
1 |
|
|
|
2 |
|
|
2 |
|
4 |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
1 |
|
2 |
|
||||||||||||||||||
Значит функция |
f x |
|
|
|
x3 |
возрастает на всей числовой прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Пример 8. Докажем, что функция |
f |
x |
sin x возрастает на отрезке |
|
|
; |
|
. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. Пусть |
|
|
|
|
|
x1 |
x2 |
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
f |
x |
|
|
f x |
|
|
|
sin x |
|
sin x |
2sin |
x2 |
x1 |
|
cos |
x2 |
|
x1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как x1 |
|
|
|
, |
x2 |
|
|
, |
|
x1 |
x2 , |
то |
|
x1 |
|
|
x2 |
|
|
|
|
, а так как |
|
|
|
|
x1 |
, |
|
|
|
|
x2 |
, то |
|
|
x1 |
x2 |
|
|
. |
|||||||||||||||||
2 |
2 |
|
|
|
2 |
|
2 |
|
2 |
|
|
2 |
|
|
2 |
|
2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Значит, |
|
|
|
x1 |
x2 |
|
|
|
|
|
, а потому cos |
x1 |
|
x2 |
|
0 . С другой стороны, из x |
x |
|
получаем, что |
|||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
