3173

Выделим ячейки B17:D17 для размещения искомых переменных y1, y2 и y3. Математические выражения левых частей ограничений введём в ячейки Е13:Е15 с помощью функции =СУММПРОИЗВ из категории Математические. Целевую функцию, как сумму искомых переменных введём в

ячейку Е17. Заполним диалоговое окно программы Поиск ре-

шения из меню Сервис (рис. 44).

Рис. 44. Заполнение диалогового окна Поиска решения

71

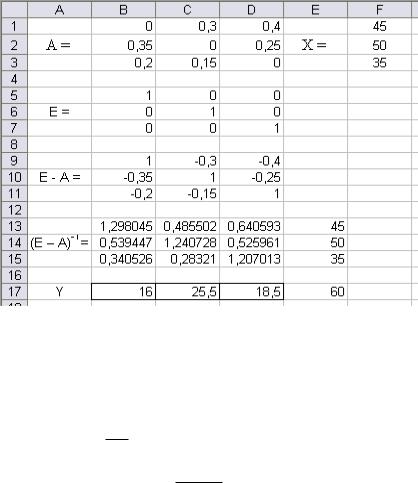
Нажав на кнопку Параметры в диалоговом окне надстройки

Поиск решения, укажем с помощью “галочек”: Линейная модель и Неотрицательные значения. Результаты отыскания вектора конечной продукции Y представлены на рис. 45.

Рис. 45. Результата решения задачи межотраслевого баланса

Смешанная задача межотраслевого баланса

Для решения третьей задачи баланса все отрасли разделим на две группы. К первой группе отнесем отрасли, для которых задан конечный продукт. Множество номеров этих отраслей обозначим

индексами i, j = 1, m . Ко второй группе отнесем отрасли, для которых задан валовой выпуск. Множество номеров этих отраслей обозначим индексами i, j = m 1, n . Тогда вектор валовых выпусков можно разделить на два подвектора

72

где Х1 – искомый подвектор с элементами Хi(i = 1, m );

X2 - заданный подвектор с элементами Хi(i = m 1, n ).

Аналогично вектор конечного продукта можно разделить на два подвектора

Y

Y = 1 , (3.12)

Y2

где Y1 – подвектор с известными значениями Yi(i = 1, m ); Y2 - подвектор с неизвестными значениями

Из второго уравнения найдем

73

Найдя из выражения (3.16) Х1 и подставив в выражение (3.17), получим Y2.

Пример. Три отрасли выпускают продукцию, причем нормы затрат ресурсов заданы матрицей А:

Конечный продукт первой отрасли равен 8 ед., объем производства второй отрасли равен 10 ед., а третьей – 15 ед. Определить объем производства первой отрасли и конечный продукт второй и третьей.

Решение. Согласно изложенному ранее первая отрасль входит в первую группу, а вторая и третья – во вторую группу, тогда

Таким образом, валовой выпуск первой отрасли равен 12 ед., конечный продукт второй и третьей равен 3,1 ед. и 9,8 ед. соответственно.

74

Коэффициенты полных материальных затрат

Запишем модель в матричной форме АХ + Y = Х .

Отсюда вектор валовых выпусков

Х = (Е – А)-1 Y.

Обозначим матрицу (Е – А)-1 через В, а ее элементы

Коэффициенты полных материальных затрат bij показывают общую потребность в продукции i–й отрасли, которая обеспечивает выпуск единицы конечной продукции j–й отрасли.

Для определения матрицы коэффициентов полных материальных затрат существуют две формулы: точная и приближенная.

Формула для точного расчета

Формула для приближенного расчета получается при разложении матрицы (Е – А)-1 в ряд Тейлора

Коэффициенты косвенных затрат

Косвенные затраты относятся к предшествующим стадиям производства и входят в продукт не непосредственно, а через затраты сопряженных отраслей (рис. 46).

Коэффициенты косвенных затрат характеризуют количество продукции i–й отрасли, которая направляется в j–ю отрасль для производства единицы ее продукции, проходя k промежуточных стадий.

75

– порядок косвенных затрат.

Для определения косвенных затрат первого порядка в матричной форме используют следующую формулу:

А(1) = А А = А2.

Матрица коэффициентов косвенных затрат второго по-

рядка

А(2) = А3.

Матрица коэффициентов косвенных затрат k-го порядка

Для получения точной расчетной формулы для суммарных косвенных затрат воспользуемся формулой (3.20):

В = Е + А + А2 + … + Аk + … = Е + А + А (k).

Отсюда получим А (k) = В – Е – А.

Для автоматизации расчёта задачи межпродуктового баланса возможно использование программы «Межотраслевая балансовая модель В.Леонтьева» из ППП PRIMA.

76

Исходными данными для расчётов является матрица коэффициентов прямых затрат, вектор известных значений конечного продукта и вектор известных значений валового выпуска (рис. 47).

Рис. 47. Ввод исходных данных в диалоговую форму

Результаты расчёта параметров модели межпродуктового баланса представлены на рис. 48.

77

-давать экономическую интерпретацию полученных результатов решения задач линейного программирования;

-применять методы линейного программирования для решения практических задач;

владеть:

-математическим аппаратом линейного программирова-

ния;

-практическими навыками формулирования и решения задач линейного программирования, в том числе с помощью ЭВМ.

Раздел математических методов, в котором рассматриваются способы решения задач на нахождение экстремума функции цели при ограничении области допустимых значений в форме уравнений или неравенств, называется математическим программированием. Другими словами, математическое (оптимальное) программирование рассматривает задачи планирования, распределения ограниченных ресурсов наилучшим образом, для достижения поставленных целей.

Общая задача математического программирования имеет вид:

определить экстремум функции

f(x) extremum (max, min),

при выполнении условий

gi(x) = ( , )bi, (i = 1, m ),

x = (x1, x2,… xj …xn), xj 0, (j = 1, n ),

где f(x) – целевая функция;

gi(x) - функция ограничения;

bi - действительное число, константа ограничения. Если функции f(x) и gi(x) представлены в виде линей-

ных функций, то оптимизационная задача называется задачей линейного программирования.

Таким образом, линейное программирование – это область математического программирования, посвященная тео-

79