Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Управление самолетом в турбулентной атмосфере. Пентюхов В.И., Мищенко Е.В

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.67 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

Системы уравнений (1.51) и (1.52) в общем случае связаны между собой, так как коэффициенты статистической линеаризации h 0 и h1 зависят как от величины полезных сигналов, так и от

величины дисперсии турбулентных возмущений сигналов на входах нелинейных элементов.

Поэтому в общем случае эти две системы уравнений надо рассматривать совместно.

Если управляющие воздействия отсутствуют 0 , т.е.

в y

рассматриваемая система работает только в режиме стабилизация, то математические ожидания (средние значения) полезных составляющих параметров движения тождественно равны нулю.

В этом случае коэффициенты статистической линеаризации зависят только от дисперсии турбулентных возмущений сигналов на входах нелинейных элементов, и система уравнений (1.52) может рассматриваться независимо от системы уравнений (1.51), которая обращается в этом случае в тождество.

Системы уравнений (1.51) и (1.52) можно представить в матричной форме.

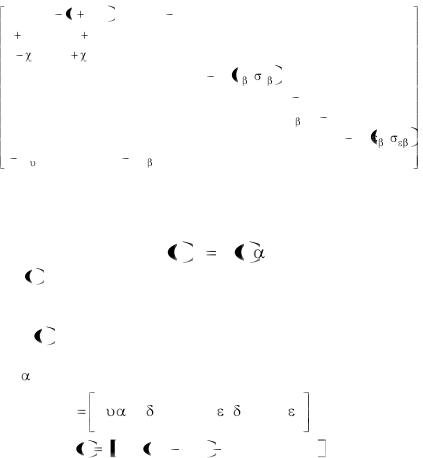
Система уравнений (1.51) в матричной форме имеет вид:


		D p X A	y	(1.53)
			y
где D p	- собственная матрица системы уравнений (1.51);
X	- матрица-столбец полезных составляющих параметров
	движения самолета;
A	- матрица-столбец коэффициентов при управляющих
	воздействиях руля высоты;

в y - управлявшее воздействие руля высоты.

При этом согласно (1.51) имеем

XT	p	n y в zвsвYв в ;	(1.54)

AT	00001000;		(1.55)

1	p n 26	0	n 27	0	0	0	0
p n33	n35p n36	0	n37	0	0	0	0
	p	1	0	0	0	0	0
0	0	0	1	h 0 Z ; z	0	0	0
0	0	0	0	1	1	0	0
0	0	0	0	0	T p	1	0
0	0	0	0	0	0	1	h 0 ;
K	0	K n	0	0	1	0	1

						(1.56)
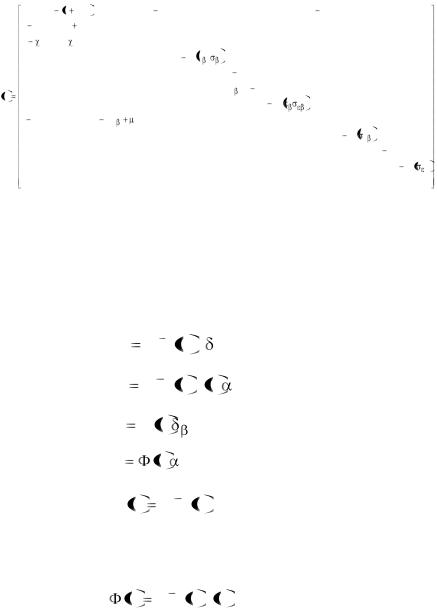
Система уравнений (1.52) в матричной форме имеет вид:
			0
		D p X		B p	T	(1.57)
					T
где D p - собственная матрица системы уравнений (1.52);
X0 - матрица-столбец турбулентных возмущений параметров
движения самолета;
B p - матрица-столбец			коэффициентов при			турбулентных
	возмущениях утла атаки;
T - турбулентное возмущение угла атаки.
0 T		0 0 0 0 0 0 0 0 0 0 0 0				(1.58)
X	p	n y в Zв sв Ув в 3 Z3 У3 3 ;				(1.58)
X	p	n y в Zв sв Ув в 3 Z3 У3 3 ;
BT p		n 26p n33	n35	n36 000000000;		(1.59)

	1	p n26	0		n27	0	0	0	0	n28	0	0	0
	p n33	n35p n36	0		n37	0	0	0	0	n38	0	0	0
		p	1		0	0	0	0	0	0	0	0	0
	0	0	0		1	h1 Z ;	0	0	0	0	0	0	0
	0	0	0		0	1	1	0	0	0	0	0	0
D p	0	0	0		0	0	T p	1	0	0	0	0	0
D p	0	0	0		0	0	0	1	h1	0	0	0	0
	0	0	0		0	0	0	1	h1	0	0	0	0
	Ki	0	Kn	Kn	0	0	1	0	1	0	0	0	0
	0	0	0		0	0	0	0	0	1	h1 z	0	0
	0	0	0		0	0	0	0	0	0	T3p	1	0
	0	0	0		0	0	0	0	0	0	0	1	h1 3
	0	0	Kn		0	0	0	0	0	0	1	0	1

(1.60)

Передаточные функции для параметров движения самолета с рассматриваемой системой стабилизации по отношению к управляющим и возмущающим воздействиям могут быть получены как решения матричных уравнений (1.53) и (1.57).

Как известно, решение этих уравнений имеет, вид:

					1
		X		D	1		p A вy ;		(1.61)
0			D 1 p B p
	X		D 1 p B p					T	(1.62)
								T
Уравнения (1.61) и (1.62) можно записать в виде:
									(1.63)
	X		Y p				y ;		(1.63)
0									(1.64)
X				p			T ,		(1.64)
где
							1 p A		(1.65)
	Y p					D	1 p A		(1.65)

–матрица-столбец передаточных функций для полезных составляющих параметров движения самолета по отношению к управляющему воздействию руля высоты;

p D 1 p B p

(1.66)

–матрица-столбец передаточных функций для турбулентных возмущений параметров движения самолета по отношению в турбулентному возмущению угла атаки.

Значение обратной матрицы D 1 p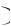равно

,i 8 ,

(1.67)

Di ,

D p

где

определитель матрицы D p ;

D p

- матрица, составленная из алгебраических дополнений

Di,k

p для элементов матрицы

p .

Индекс i определяет номер строки, а индекс к номер столбца,

где

расположен

элемент матрицы

p ,

для которого

получено

алгебраическое

дополнение

p . В

то же время

индекс i

i,k

определяет номер столбца, а индекс k - номер строке, на пересечении которых располагается это алгебраическое дополнение как элемент

матрицы

p .

i,k

Подставляя в (1.63) значение обратной матрицы

1 p согласно

(1.67), получим

k,i 8

(1.68)

Y p

Di,k p

D p

После перемножения матриц

равенство (.1.68)

Di,k

принимает вид

Y p

D5,k

k 8

(1.69)

D p

При этом согласно (1.55) и (1.56) имеем;

a0p3

a1p2

(1.70)

a 2p

a3;

;

c p

;

Z ;

p d

;

e p2

Z ;

p e

;

k 8

D5,k p

e p2

p e

;

0p2

1p1

h0 Z ; z

;

f2 ;

T h

Z ;

;

p ;

T h

Z ;

p ;

(1.71)

a0 T ; a1

;

1 h0 Z ; z

0K n

(1.72)

2 ; a 2

;

h0 Z

;

3K n

h0 Z ; z

6 ; a3

;

h0 Z ; z

9K n ;

;

8; c0

T n 27 ;

;

n 27

n37

n 27n33 ;

(1.73)

;

n37

n 27n33 ; d0

0 ;

;

3; d2

;

9 ;

;

3; e0

T ; e1

;

2 ;

;

6 ; e3

;

6 ;

0 ; f1

3K n

5K ; f2

9K n ;

0	n 27	;	2	n 26	n33	n35 ;	3	n 27	n33 n35	;
	n37		n 27n35 ;		6 n36 n 26n33;				n 26n37	(1.74)
5	n37		n 27n35 ;		6 n36 n 26n33;			8	n 26n37
n 27n36		;	9	n 26n37		n 27n36

Аналогично значение обратной матрицы D 1 pравно:

k,i

(5.75)

D p

Di,k

где D p - определитель матрицы D p ;

Di,k p

матрица,

составленная из

алгебраических

дополнений D

i,k

для элементов матрицы D p .

Подставляя в (1.64) значение матрицы D 1 p

согласно (1.75),

получим:

Di,k

k,i

B p

(1.76)

D p

После

перемножения

матриц

Di,k p

B p

равенство

(1.76)

принимает вид:

D1,k

p B11 D2,k p B21 p 1k ,i

p 1k 12

(1.77)

D p

где B

и B

p - элементы матрицы столбца B p .

При этом согласно (1.59) и (1.60) имеем

D p

a0p4

a1p3

a 2p2

a3p

a 4;

(1.78)

D1,k

p B11

D2,k

cp3

c p2

;

d p3

e p2 e

Z ;

;

p ;

;

e p

p ;

;

e p

p ;

p B21 p 1k

T h

;

e p3

;

T e

e p3

p2 ;

f p2

p ;

f p

p ;

T h

p4 f p3

p2 ;

T f

p4 f p3

;

a 0

T T3; a1

T h1

3 1 h1 z3 1K n

T3h1

;

1 h1 Z ; z

0 K n

K n

T T3 2 ; a 2

T h1

4h1 z3 1K n

T3h1

;

h1 Z ; z

3 K n

K n

h1 Z ; z

T T3 6

;

3 1 h1 z3 1K n

h1 Z ; z

0 K n

K n ;

a3 T h1

7h1 z3 1Kn

T3h1

;

h1 Z ; z

K n

;

h1 Z ; z

5K h1 Z ; z

3 K n

h1 z3 4Kn

h1 Z ; z

h1 z3 10Kn K ;

(1.79)

(1.80)

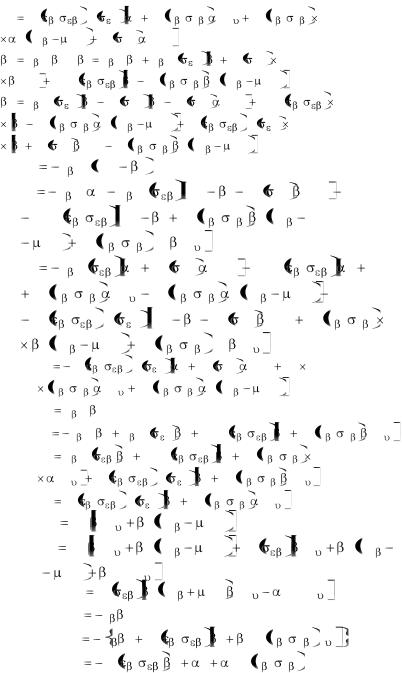
a 4

;

h1 Z ; z

9 K n

K n

h1 z3 7K n ;

T T3 1;

T T3 5

T h1

3 1 h1 z3

3K n

T3h1

;

1 h1 Z ; z

2 K n

K n ;

T h1

3 5

h1 z3 5 h1 z3 7K n

T3h1

;

h1 Z ; z

9 K n

K n

;

h1 3

h1 z3 3K n h1 Z ; z

2 K n

K n ;

T T3 n 26

1 ;

T T3 6

T h1

n 26

h1 z3 3K n

T3h1

;

n 26

h1 Z ; z

2 K n

(1.81)

K n

h1 Z ; z

n 27 1K ;

T n1

h1 z3 7K n

T3h1

;

h1 Z ; z

9 K n

K n

;

3 n 26

h1 z3 3K n

h1 Z ; z

2 K n

K n

h1 Z ; z n 27 1K ;

;

h1 z3 7Kn

Z ; z

h1 Z ; z

9 Kn

Kn ;

T T3

T T3 4

T h1

3 0

T3h1

;

h1 Z ; z 2K ;

T h1

T3h1

;

h1 Z ; z

;

3 0

h1 Z ; z

2K ;

;

3 4

h1 Z ; z

9K ;

T3 1K

0 Kn

Kn ;

T3 5K

4 Kn

1K 0 Kn

3Kn K

;

4 Kn

Kn 5K

7Kn K ;

0Kn ;

(1.81)

;

2h1 Z ; z K Kn ;

;

9h1 Z ; z

Kn ;

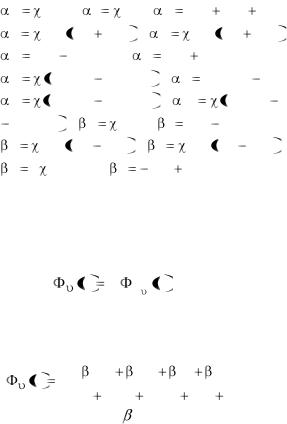
0	n 27 ;	1	28 ;		2 n 26 n33		n35 ;
3	n 27 n33		n35 ;		4	n 28 n33	n35 ;
5	n37	n 27 n35 ;		6	n36	n 26n33;	(1.82)
7	n 28n36		n 26n38 ;		8	n 26n37	n 27 n36 ;

9	n 26n37	n 27 n36 ;		10	n 28n37
n 27 n38 ; 0		n 26 ;	1	n33	n35 ;
2	n 27 n33	n35 ;	3	n 28	n33 n35 ;
4	2 n 26n33;	5	n36	n 26n33;

Между передаточными функциями для угла атаки самолета по отношению к турбулентному возмущению угла атаки и для угловой скорости тангажа по отношению к турбулентному возмущению угла атаки существует следующая связь:

p	1		p ;	(1.83)
		p
	p

Из (1.77) и (1.83) следует, что передаточная функция для угли тангажа самолета по отношению к турбулентному возмущению угла атаки равна:

0p3

1p2

(1.84)

a p3

p a

Коэффициенты а

, входящие

(1.84), определяются

согласно (1.80) и (1.61).

Таким образом, равенства (1.65),(1.77) и (1.84) определяют передаточные функции для всех параметров, входящих в уравнения (1.51) и (5.52), как по отношению к управляющим воздействием руля высоты, так и по отношению к турбулентным возмущениям угла атаки.

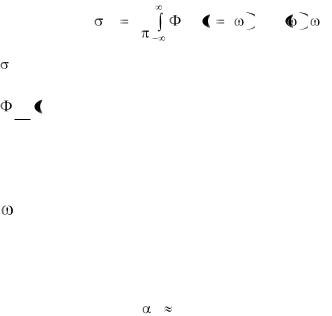
Дисперсия турбулентных возмущений параметров движения самолета с двухканальной векторной системой

непосредственного управления подъемной силой.

Полученные выше передаточные функции для параметров движения самолета по отношению к турбулентному возмущению угла атаки позволяют определить дисперсию турбулентных возмущений этих параметров.

Действительно (см. [18, 19] и др.), дисперсия турбулентного возмущения любого параметра движения самолета при действии на него вертикальных порывов может быть определена с помощью следующего равенства:

2 zk

1				2		(1.85)
				2
			p j	Sw	d
2	z		p j	Sw	d
2		k			y
	Wy

где zk - среднеквадратическое значение турбулентного возмущения

k-го параметра движения самолета;

zk p- передаточная функция для k-го параметра движения

самолета по отношению к скорости вертикальных порывов;

SWy - спектральная плотность скорости вертикальных

порывов;

- угловая частота колебаний самолета, вызванная вертикальными порывами.

Как было показано выше, турбулентное возмущение угла атаки в центре тяжести самолета, вызванное скоростью

вертикальных порывов, приближенно равно:
		T	Wy	(1.86)
		T	V0
			V0
где W	y	- скорость вертикальных порывов;
	y

V0 - скорость полета самолета.

С учетом (1.86) равенство (1.85) можно представить в виде

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]