2893

ВВЕДЕНИЕ

В настоящем пособии в сжатой форме излагаются основные понятия теории функций комплексного переменного. Понятие комплексного числа возникло в первую очередь в результате потребностей автоматизации вычислений. Даже простейшие алгебраические операции над действительными числами выводят за пределы области действительных чисел. Как известно, не всякое алгебраическое уравнение может быть разрешено в действительных числах. Тем самым надо или отказаться от автоматического применения установленных методов решения и каждый раз проводить подробное исследование возможности их применения, или расширить область действительных чисел с тем, чтобы основные алгебраические операции всегда были выполнимы. Таким расширением области действительных чисел являются комплексные числа. Замечательным свойством комплексных чисел является тот факт, что основные математические операции над комплексными числами не выводят из области комплексных чисел.

Введение комплексных чисел и функций комплексной переменной удобно также при интегрировании элементарных функций, при решении дифференциальных уравнений и т. д., где часто приходится выходить в область комплексных чисел. Комплексная форма записи оказывается удобной и при математической формулировке многих физических положений (например, в электро- и радиотехнике, электродинамике и т.

д.).

Один из основных классов функций комплексной переменной — аналитические функции — находится в тесной связи с решениями уравнения Лапласа, к которому приводятся многие задачи механики и физики. Поэтому методы теории функций комплексной переменной нашли весьма широкое и эффективное применение при решении большого круга задач гидро- и аэродинамики, теории упругости, электродинамики и других естественных наук.

3

1. КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ 1.1. Комплексные числа

Комплексным числом z называется упорядоченная пара

( y, x) , т.е. важны не только значения чисел х и у,

составляющих пару, но и порядок, в котором эти числа расположены.

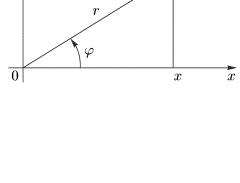
Комплексные числа имеют простой геометрический смысл. Возьмем на плоскости прямоугольную декартову

частью числа z и обозначается x = Re z ; вторая компонента у

называется мнимой частью числа z и обозначается у = Im z. (Термины "действительная" и "мнимая" часть напоминают о непростом развитии теории комплексных чисел; теперь нам очевидно, что первая координата точки z не более "вещественна", чем вторая.) Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью и обозначается через . Два комплексных числа z1 = (x1 ,y1 ) и z 2 = (x 2 ,y 2 ) считаются равными, если x1 = x2 ,

4

y1 = y2 (т.е. если соответствующие точки z1 и z 2 на плоскости

совпадают).

Комплексные числа z = (x,0) изображаются точками на оси ОХ, как и действительные числа. Поэтому ось ОХ

точками на оси OY. Эта ось (в дань исторической традиции)

называется мнимой осью, а числа z = (0, y) — чисто мнимыми.

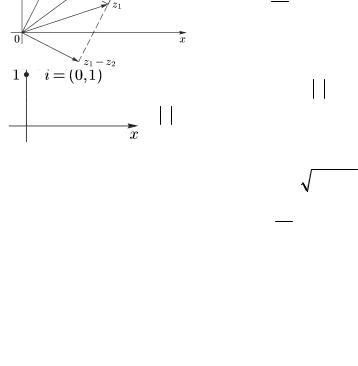
Комплексное число (0,1) называется мнимой единицей и обозначается через i : i = (0,1) (рис. 1.2).

Иногда удобно представлять комплексное число z = (x,у)

в виде вектора Oz с координатами (х,у), исходящего из начала координат (т.е. в виде радиус-вектора точки z). Длина этого вектора называется модулем числа z

и обозначается через z . Таким образом, z равен расстоянию от точки z до начала

координат. По теореме Пифагора (см.

рис. 1.1)

вектором Oz , отсчитанный против часовой стрелки, называется аргументом комплексного числа z и обозначается через Arg z. Для числа z = 0 значение Arg z не определено. Очевидно (см. рис. 1.1), что

Рис. 1.3

откуда

5

Удобно ввести главное значение аргумента числа z - значение аргумента, удовлетворяющее неравенству −π <ϕ ≤π . Главное

значение аргумента числа z обозначается через arg z.

В дальнейшем вектор Oz мы часто будем обозначать просто z.

1.2. Действия над комплексными числами

1. Сумма, разность комплексных чисел и умножение комплексного числа на действительное число определяются точно так же, как действия над соответствующими векторами.

z = z1 + z2 = (x1 + x2 , y1 + y2 )

Разностью комплексных чисел называется комплексное число z = z1 − z2 = (x1 − x2 , y1 − y2 ) .

Таким образом, при сложении и вычитании комплексных чисел соответственно складываются или вычитаются их действительные и мнимые части. Из рис. 1.3 видно, что модуль

z1 − z2 равен расстоянию между точками z1 и z 2 .

Произведением комплексного числа z = (x,у) на действительное число λ называется комплексное число λ z = ( λ х, λ у).

Так как (см. рис. 1.3) сторона Oz треугольника Ozz1 не

больше суммы двух других его сторон, то справедливо так называемое неравенство треугольника:

6

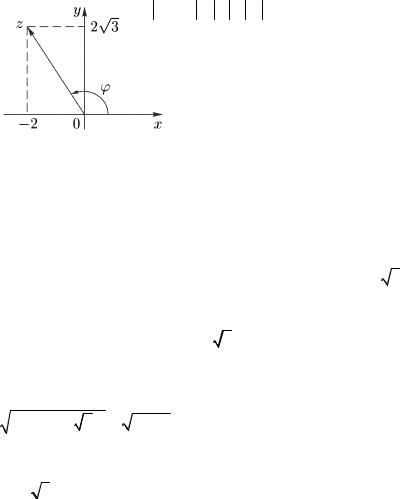
z1 + z2 ≤ z1 + z2 ;

равенство имеет место тогда и только тогда, когда векторы z1

декартовой формой комплексного числа z. Сделав подстановку по формулам (1.2), придем к выражению

7

аргумента ϕ = 23 π . Поэтому число z в тригонометрической форме имеет вид

Можно использовать и другие значения Arg z:

2. Рассмотрим теперь операцию умножения комплексных

z1 = x1 +iy1 и z2 = x2 +iy2 , записанных в алгебраической форме,

определяется следующим образом. Следует раскрыть скобки по обычным алгебраическим правилам и упростить

полученное выражение, пользуясь равенством i2 = −1:

лучше не запоминать эту формулу, а выполнять указанные выше действия непосредственно.

Пример 2.2. Найти произведение чисел z1 = 2 −3i и z2 = −4 +i .

Решение.

z1z2 = (2 −3i)(−4 +i) = −2 4 +3 4 i +2 i −3 i2 =

= −8 +12i + 2i +3 = −5 +14i .

Из определения суммы и произведения комплексных чисел следует, что эти операции обладают теми же свойствами, что и соответствующие операции над действительными числами:

8

z1 + z2 = z2 + z1; z1z2 = z2 z1;

z1 (z2 + z3 ) = z1z2 + z1z3; z1 (z2 z3 ) = (z1z2 )z3.

Отсюда следует, в частности, что при действиях над комплексными числами применимы все формулы сокращенного умножения. Например:

(z1 + z2 )2 = z12 +2z1z2 + z22 , (z1 + z2 )(z1 − z2 ) = z12 − z22 ,

Два комплексных числа, у которых действительные части

3. Деление комплексных чисел, так же как и для действительных чисел, определяется как действие, обратное умножению. Делить можно только на комплексные числа, отличные от нуля. Чтобы найти частное z1 / z2 комплексных

чисел, заданных в алгебраической форме, следует домножить

числитель и знаменатель дроби на z2 и воспользоваться равенством (2.4):

9

После этого нужно выполнить умножение в числителе и разделить действительную и мнимую части получившегося числа на знаменатель:

Как и в случае умножения, мы рекомендуем не запоминать эту формулу, а усвоить правило нахождения частного.

(заметим, что мы выполнили действие, обратное умножению из примера 2.2).

4. Рассмотрим теперь умножение и деление комплексных чисел, заданных в тригонометрической форме. Пусть

+i(sin ϕ1 cos ϕ2 +cos ϕ1 sin ϕ2 )) = r1r2 (cos (ϕ1 +ϕ2 ) +i sin (ϕ1 +ϕ2 )). (2.5)

Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы складываются:

z1z2 = z1 z2 ,

10