4. Ачх механической части гиросистемы с оптимальными параметрами m* и с*.
При помощи пакета Matlab6.1 построим АЧХ ПФ как объекта стабилизации без учёта вязкого трения в опорах.
Рис 5
АЧХ механической части системы при
оптимальном значении С* и *
5. Синтез цепи обратной связи. Лчх разомкнутой цепи.
Определение требуемого Кст.
Из условия заданной статической устойчивости и необходимых запасов устойчивости определим значение Kст:
ЛЧХ разомкнутой цепи.
Рассмотрим ПФ ГИЛУ как системы управления.
Данная
ПФ характеризует замкнутую систему.
ПоложивK(s)=0
получим выражение для ПФ ГИЛУ без
обратной связи. Учтя это, выражение для
ПФ разомкнутой системы будет иметь вид:
Подставим численные значения в данные выражения. (Знак «-» в числителе выносится за пределы обратной связи, следовательно, в разомкнутой ПФ не учитывается):
Для полученной ПФ построим ЛЧХ:
Рис 6
ЛЧХ разомкнутой ПФ как системы управления
с требуемым Kст.
Замкнутая система не устойчива!
Необходимо использовать корректирующий контур (КК) в цепи обратной связи (K(s)) для достижения статической устойчивости и требуемого качества.
Синтез КК цепи ОС.
Для коррекции системы воспользуемся интегро-дифференцирующим фильтром:
ЛЧХ фильтра приведена на Рис 7а.
Выберем следующие параметры корректирующего фильтра:
Данные параметры КК обеспечивают следующие запасы устойчивости:
По амплитуде =10дБ;
По фазе =35,10.
Рис 7
а – ЛЧХ КК;
б – ЛЧХ Скорректированной системы;
в – ЛЧХ Разомкнутой системы (приведена
для сравнения).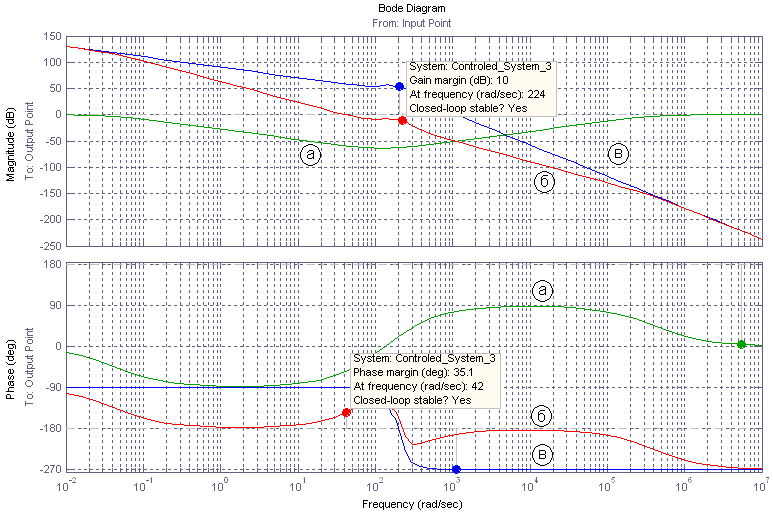
Используемый КК реализуется следующей электрической схемой:
Рис 8
Электрическая схема КК
Для приведённой схемы:
Решая данные уравнения относительно «электрических» переменных при помощи пакета Maple7 получим:
6. Переходный процесс при действии постоянного возмущающего момента.
При помощи пакета Matlab6.1 построим переходный процесс (реакция системы на единичную ступеньку на входе) скорректированной гиросистемы (M1).
Рис 9
Структурная схема ПФ ГИЛУ как системы
управления
Рис 10
ПП замкнутой ПФ ГИЛУ как системы
управления
7. АЧХ замкнутой гиросистемы.
При помощи системы Matlab6.1 построим АЧХ системы Рис 9:
Рис 11
АЧХ замкнутой системы
8. Структурная схема гиросистемы с сопутствующей нелинейностью. Разделение линейной и нелинейной части.
По исходным уравнениям составим структурную схему с нелинейностью:
Рис 12
Структурная схема ГИЛУ
Применяя к данной схеме структурные преобразования, разделим линейную и нелинейную составляющие системы:
Рис 13
Структурная схема ГИЛУ с разделёнными
линейной частью и нелинейностью
Таким образом, линейная часть ГИЛУ имеет следующую ПФ:
Подставим числовые значения параметров в приведённое выражение:
9. Обоснование возможности применения метода гармонической линеаризации. ЛАЧХ приведённой линейной части.
Построим ЛЧХ для приведённой линейной части.
Рис 14
ЛЧХ линейной части
Как видно из ЛЧХ линейная часть системы обладает свойствами фильтра, следовательно, выполняется гипотеза фильтра необходимая для применения метода гармонической линеаризации.
10. Гармоническая линеаризация нелинейной системы. Условие амплитудно-фазового баланса.
Рассмотрим линейный элемент (Рис 3). При подаче на вход гармонического сигнала, на выходе получим ступенчатый сигнал (см. Рис 15). Таким образом, нелинейность из входной гармоники (любой ненулевой амплитуды) создаёт спектр гармоник (согласно теории Фурье) с амплитудами, не зависящими от амплитуды входного сигнала.
Рис 15
Отработка сигнала нелинейным элементом
Поскольку ЛАЧХ линейной части обладает свойствами фильтра, следовательно, она будет фильтровать все гармоники кроме 1 (поскольку частоты остальных гармоник располагаются в области ЛАЧХ с сильным ослаблением). Таким образом, на вход нелинейного элемента поступит только первая гармоника.
Исходя из вышесказанного, возможно существование автоколебаний в системе.
Произведём гармоническую линеаризацию нелинейного элемента:
Пусть на вход элемента поступает сигнал:
;
Нелинейный элемент представим в виде:
;
С учётом принятой гипотезы фильтра
разложив
в
ряд Фурье получим:
где
Запишем уравнение амплитудно-фазового баланса:
