Лекция 4 Электрическое поле в диэлектрике Электрический диполь в электрическом поле

Электрический диполь – это система из двух одинаковых по модулю разноимённых точечных зарядов (+q) и (-q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля ( l << r ).

Плечо диполя вектор, направленный по оси диполя от отрицательного заряда к положительному и равный по модулю расстоянию между ними.

Электрический момент диполя вектор, совпадающий по направлению с плечом диполя и равный произведению зарядаq на плечо :

.

1) Напряжённость и потенциал поля диполя на продолжении оси диполя в точке А на расстоянии r от центра диполя (точка О).

.

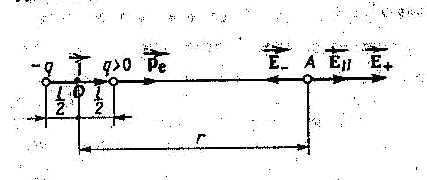
Тогда:

;

.

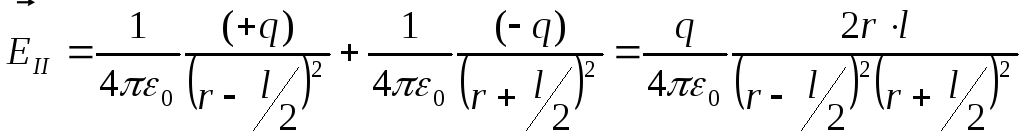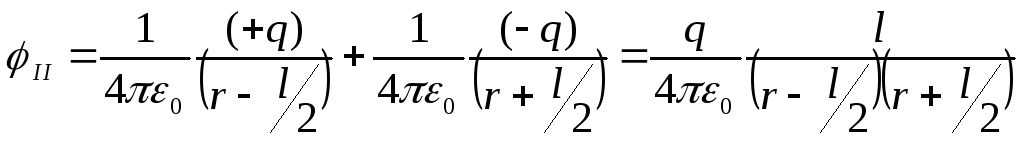Учитывая, что l << r, получаем:

;

.

2) Напряжённость и потенциал поля диполя на перпендикуляре, восстановленном к оси диполя из его середины (в точке В симметричной зарядам (+q) и (-q)) при l << r.

.

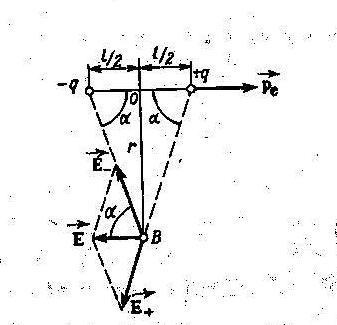
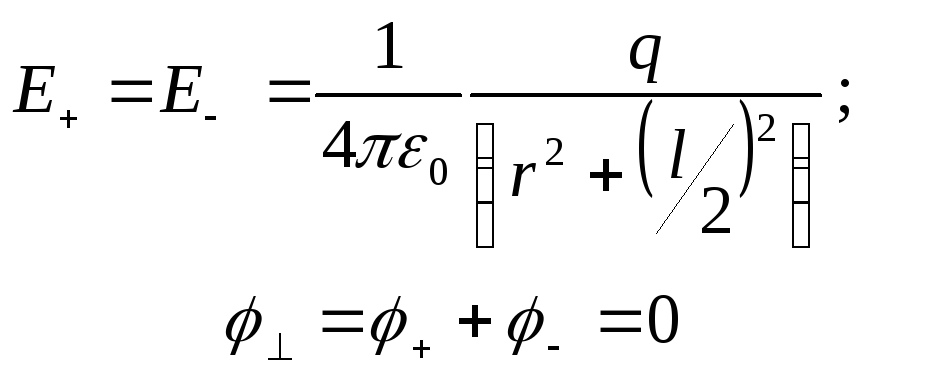При l << r .

Из подобия треугольников ;

Тогда .

и направлены в противоположные стороны.

3) Произвольное положение точки А

.

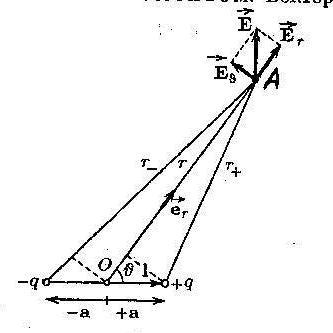
Т.к. l << r то (r – расстояние от точки А до центра диполя точки О);

.

Тогда

.

Потенциал поля диполя убывает с расстоянием быстрее, чем потенциал точечного заряда (, а не).

Напряжённость поля в точке А определяем, разложив векторна две проекции в направленияхи.

;

;

.

В частности получаем:

при ипри.

(при одинаковыхr ).

Сила, действующая на диполь в электрическом поле

В неоднородном электрическом поле силы, действующие на концы диполя неодинаковы.

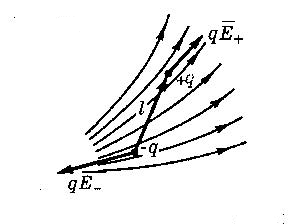
Результирующая сила , действующая на диполь равна

, где

напряжённости внешнего поля в точках, где расположены положительный и отрицательный заряды диполя.

приращение вектора на отрезке, равном длине диполяв направлении вектора.

Вследствие малости этого отрезка можно записать .

Тогда .

Сила стремится втянуть диполь в область более сильного поля.

В однородном поле результирующая силаравна нулю, но может быть не равен момент сил:

.

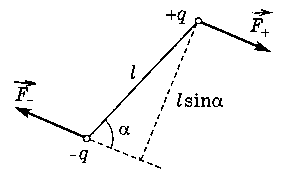
Этот момент сил стремится повернуть диполь так, чтобы его электрический момент установился по направлению внешнего поля. Такое положение диполя является устойчивым.

Энергия диполя во внешнем электрическом поле

_, где

потенциал внешнего поля в точках, где находятся положительный и отрицательный заряды диполя.

_.

Но . Тогдаи

.

Видно, что минимальную энергию диполь имеет в положении устойчивого равновесия.

Поляризация диэлектрика

Диэлектриками (изоляторами) называют вещества, практически не проводящие электрический ток.

Диэлектрики состоят либо из нейтральных молекул, либо из заряженных ионов, находящихся в узлах кристаллической решётки. Сами же молекулы могут быть полярными и неполярными. Полярные молекулы обладают собственным дипольным моментом.

Под действием внешнего электрического поля происходит поляризация диэлектрика. В неполярных молекулах происходит смещение зарядов – положительных ядер атомов по полю, а отрицательных электронных оболочек атомов против поля. Если же диэлектрик состоит из полярных молекул, то при отсутствии внешнего поля их дипольные моменты ориентированы совершенно хаотически (из-за теплового движения). Под действием внешнего поля дипольные моменты ориентируются в пространстве преимущественно в направлении внешнего поля.

В диэлектрических ионных кристаллах типа КСl , NaCl при включении внешнего поля все положительные ионы смещаются по полю, отрицательные – против поля.

Во всех перечисленных случаях включение внешнего электрического поля приводит к возникновению или переориентации дипольных моментов.

В результате поляризации на поверхности диэлектрика, а если диэлектрик неоднородный, то и в его объёме появляются нескомпенсированные заряды, которые называют поляризационными или связанными и обозначают q’; ρ’; σ’.

Заряды, которые не входят в состав молекул диэлектрика, называют сторонними или свободными. Они могут находиться как внутри, так и вне диэлектрика.

Пусть напряжённость поля сторонних зарядов;

напряжённость поля связанных зарядов.

Полем в диэлектрике называют величину, являющуюся суперпозицией полейи:

.

Для количественного описания поляризации диэлектрика естественно взять дипольный момент единицы объёма.

Поляризованностью в данной точке М пространства называют вектор :

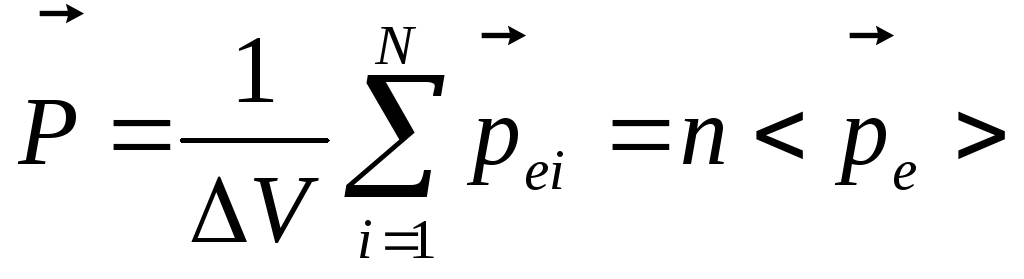, где

физически бесконечно малый объём вокруг точки М, содержащий диполей;

сумма дипольных моментов всех молекул в объёме ;

концентрация молекул;

средний дипольный момент одной молекулы.

В системе СИ поляризованность измеряется в Кл/м² .

Как показывает опыт, вектор для большинства диэлектриков линейно зависит от напряжённости поляв диэлектрике. Если диэлектрик изотропный ине слишком велико, то

, где

диэлектрическая восприимчивость вещества (безразмерная величина, характеризующая свойства самого диэлектрика). Всегда .

Для ионных кристаллов, электретов и сегнетоэлектриков зависимость отне является линейной.

Теорема Гаусса для вектора :поток вектора сквозь произвольную замкнутую поверхностьS равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объёме, охватываемом поверхностью S , т.е.

.

В дифференциальной форме Теорема Гаусса для вектора имеет следующий вид:

.

Если диэлектрик однородный и внутри него нет сторонних зарядов (ρ = 0) то и ρ’ = 0

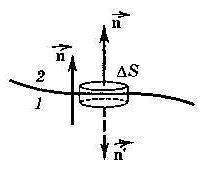
На границе раздела диэлектриков нормальная составляющая вектора испытывает разрыв, величина которого зависит от:

.

Если среда 2 – вакуум, то .