Теорема Остроградского – Гаусса в дифференциальной форме.

Применив математическую теорему Гаусса к формуле , получаем:

.

Физический смысл дивергенции (от латинского – расхождение) – истечение из данной точки (положительная дивергенция) или сток в данную точку (отрицательная дивергенция).

Лекция 3 Проводники в электрическом поле

Распределение зарядов в проводнике.

В металлических проводниках свободные носители электрического заряда (электроны проводимости) могут под действием электрического поля перемещаться по всему проводнику (электронный газ).

Перераспределение зарядов в проводнике под влиянием внешнего электростатического поля называется явлением электростатической индукции. Индуцированные (наведённые) заряды исчезают, как только проводник удаляется.

Индуцированные заряды создают дополнительное электрическое поле, которое вместе с исходным (внешним) полем образует результирующее электрическое поле, которое определяется как суперпозиция внешнего поля и поля индуцированных зарядов.

Внутри проводника т.к. перемещение зарядов под влиянием внешнего поля будет продолжаться до тех пор пока не установится определённое распределение зарядов, создающих индуцированное поле, которое полностью компенсирует внешнее поле.

Из теоремы Остроградского – Гаусса следует, что раз , то и плотность избыточных (не скомпенсированных) зарядов внутри проводника также всюду равна нулю (ρ = 0 ).

Избыточные заряды появляются лишь на поверхности проводника с поверхностной плотностью , различной в разных точках его поверхности.

Т.к. , то потенциал во всех точках внутри проводника одинаков и его поверхность эквипотенциальна, т.е. непосредственно у поверхности проводника поленаправлено по нормали к ней в каждой точке.

П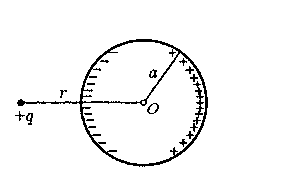ример 1 Найдём потенциал незаряженного проводящего шара, на расстоянии r от центра которого расположен точечный заряд q.

Потенциал всех точек шара одинаков, поэтому будем искать его в точке О:

, где

потенциал в точке О от всех положительных и отрицательных зарядов на поверхности шара.

Таким образом, для потенциала шара получаем .

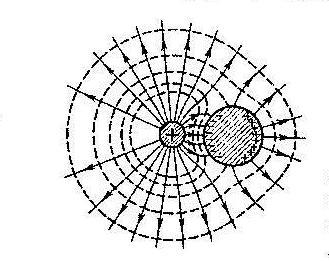
Пример 2 Поле для системы из двух проводящих шаров, один из которых заряжен. Вследствие электрической индукции на правом (незаряженном) шаре произошло разделение зарядов противоположного знака.

Электрическое поле у поверхности проводника

В качестве замкнутой поверхности выбираем небольшой цилиндр с площадью оснований , расположенный так, чтобы его ось была направлена по нормали к поверхности проводника.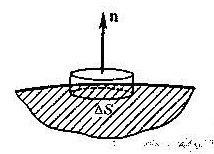

Потоки вектора через боковую поверхность и внутренний торец равны нулю. По теореме Гаусса имеем

, где

локальная поверхностная плотность заряда на проводнике;

проекция вектора на внешнюю нормаль.

Силы, действующие на поверхность проводника

Пусть заряженный участок поверхности проводника граничит с вакуумом. На малый элемент с зарядомдействует сила, гденапряжённость поля, создаваемого всеми остальными зарядами системы в месте нахождения заряда. Причёмне равно напряжённостиполя вблизи данного элемента поверхности проводника.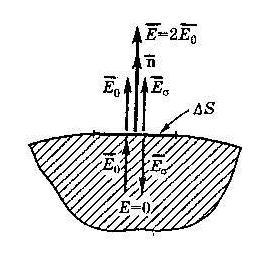

Если напряжённость поля, создаваемого зарядомв точках очень близких к площадке, так, что можно принять её за бесконечную равномерно заряженную плоскость, то. Результирующие поле определяем по принципу суперпозиции:

.

Внутри проводника и. Тогда вне проводника.

Следовательно .

Сила, действующая на единицу поверхности проводника (поверхностная плотность сил или электрическое давление)

.

Учитывая, что илиполучаем

.

Независимо от знака , а значит и направления, силы электрического давления всегда направлены наружу проводника, стремясь его растянуть.

Пример 1 Определить поверхностную плотность сил, растягивающих сферу радиусом R и с зарядом q.

, тогда .

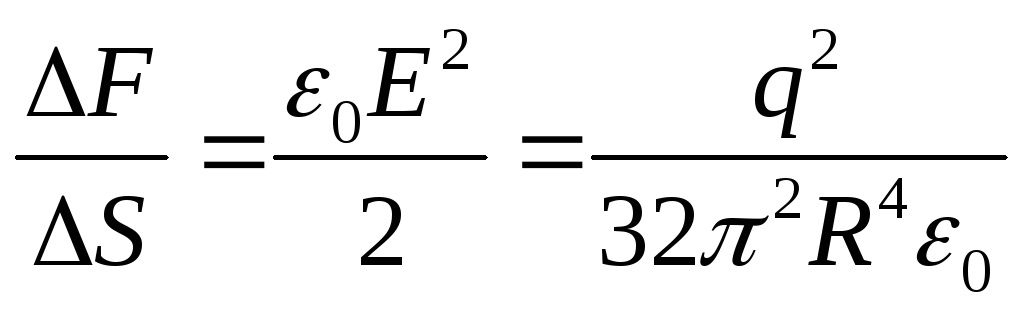Пример 2 Найти выражение для электрической силы, действующей в вакууме на проводник в целом, полагая, что известна напряжённость поля во всех точках у поверхности проводника.

, где .

Результирующая сила, действующая на весь проводник, определяется интегрированием этого выражения по всей поверхности проводника

.