
- •Электромагнетизм Некоторые сведения из математики
- •Лекция 1 электростатика
- •Лекция 2
- •1) Поле равномерно заряженной бесконечной плоскости.
- •2) Поле двух бесконечных параллельных плоскостей, заряженных равномерно разноимёнными зарядами с плотностями и .
- •Теорема Остроградского – Гаусса в дифференциальной форме.
- •Лекция 3 Проводники в электрическом поле
- •Электрическое поле у поверхности проводника
- •Силы, действующие на поверхность проводника
- •Свойства замкнутой проводящей оболочки
- •Общая задача электростатики. Уравнение Пуассона
- •Электроёмкость Электроёмкость уединённого проводника
- •Лекция 4 Электрическое поле в диэлектрике Электрический диполь в электрическом поле
- •Сила, действующая на диполь в электрическом поле
- •Поляризация диэлектрика
- •Вектор электрического смещения
- •Поле на границе раздела диэлектриков
- •Поле на границе проводник – диэлектрик
- •Некоторые важные следствия по теме:
- •Лекция 5 Энергия электрического поля
- •Постоянный электрический ток –
- •Уравнение непрерывности
- •Разветвлённые цепи
- •Закон Джоуля–Ленца
- •1). Однородный участок цепи
- •2). Неоднородный участок цепи
- •Лекция 6 Магнитное поле в вакууме
- •Магнитное поле равномерно движущегоя заряда
- •Закон Био – Савара
- •Основные законы магнитного поля
- •1). Магнитное поле прямого тока I:
- •2). Магнитное поле соленоида, по которому протекает ток I:
- •3). Магнитное поле тороида:
- •Лекция 7 Проводники с током в магнитном поле Закон Ампера
- •Момент сил, действующих на контур с током
- •Магнитное поле в веществе
- •Вектор вектор напряжённости магнитного поля
- •Магнитное поле на границе раздела магнетиков
- •Лекция 8
- •Движение заряженных частиц в электрическом и
- •Магнитном полях
- •Движение заряженных частиц в постоянном магнитном поле
- •Отклонение движущихся заряженных частиц электрическим и магнитным полями
- •Ускорители заряженных частиц
- •Преобразования Лоренца для электрических и магнитных полей
- •Электромагнитная индукция
- •Природа электромагнитной индукции
- •Явление самоиндукции
- •Взаимная индукция
- •Энергия магнитного поля
- •Магнитное давление
- •Лекция 10 Уравнения Максвелла для электромагнитного поля
Электромагнетизм Некоторые сведения из математики
Оператор «набла»
(оператор Гамильтона)
–
![]() .
.
Градиент
скалярной величины
![]() .
.
Дивергенция
вектора
![]() (скалярная величина)
(скалярная величина)
![]()
![]() .
.
Ротор вектора
![]() –
–![]()
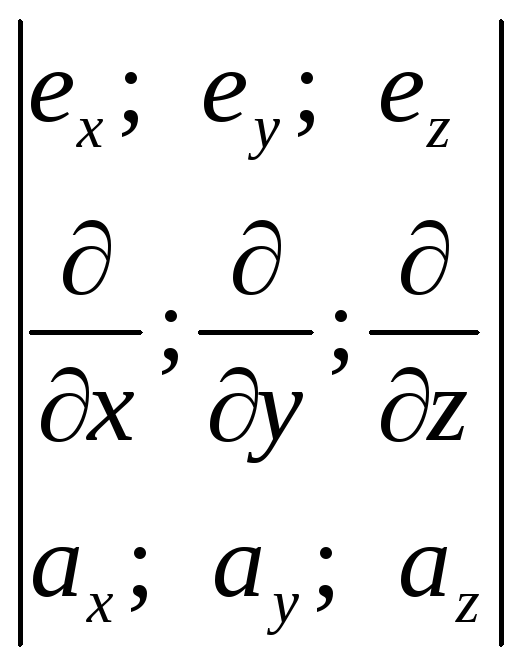 =
=
=
![]()
![]() .
.
Теорема Гаусса
Поток
вектора
![]() , характеризующего какое-либо поле,
через произвольную замкнутую поверхность
S
, мысленно проведённую в этом поле, равен
интегралу от дивергенции вектора
, характеризующего какое-либо поле,
через произвольную замкнутую поверхность
S
, мысленно проведённую в этом поле, равен
интегралу от дивергенции вектора
![]() ,взятому
по объёму V,
ограниченному замкнутой поверхностью
S
,взятому
по объёму V,
ограниченному замкнутой поверхностью
S
![]() .
.
Теорема Стокса
Циркуляция вектора
![]() ,характеризующего
какое-либо поле, вдоль произвольного
замкнутого контура l
, мысленно проведённого в этом поле,
равна потоку
ротора
вектора
,характеризующего
какое-либо поле, вдоль произвольного
замкнутого контура l
, мысленно проведённого в этом поле,
равна потоку
ротора
вектора
![]() через
поверхность S
, натянутую на контур l
.
через
поверхность S
, натянутую на контур l
.
![]() .
.
Лекция 1 электростатика
Электрический заряд.
Все тела в природе способны электризоваться, т.е. приобретать электрический заряд.
Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Заряды условно различают на положительные и отрицательные. Точечные заряды одного знака отталкиваются, разных знаков – притягиваются друг другом.
Заряд заряженных элементарных частиц (электронов, позитронов и протонов) одинаков по абсолютной величине и представляет собой наименьший встречающийся в природе электрический заряд, называемый элементарным зарядом
![]() .
.
Всякий заряд образуется совокупностью элементарных зарядов и является целым кратным е:
q = N.e
т.е. электрический заряд «квантуется».
Закон сохранения электрического заряда: суммарный заряд электрически изолированной системы не может изменяться.
Этот закон тесно связан с релятивистской инвариантностью заряда т.е. величина заряда не зависит от того движется этот заряд или покоится.
Закон Кулона: сила взаимодействия двух неподвижных точечных зарядов, находящихся в вакууме, прямо пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей заряда прямой
Точечным зарядом называют заряженное тело, размерами которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрический заряд.
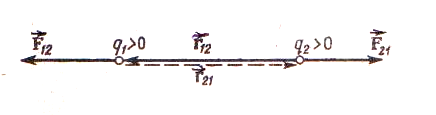
![]()
![]() сила,
действующая на заряд q1
со стороны
заряда
q2
сила,
действующая на заряд q1
со стороны
заряда
q2
![]() ;
;
![]() вектор, направленный
от q2
к q1
;
вектор, направленный
от q2
к q1
;
![]() электрическая
постоянная,
относящаяся к числу
фундаментальных
физических постоянных
электрическая
постоянная,
относящаяся к числу
фундаментальных
физических постоянных
![]() .
Здесь Ф
– – размерность электрической
ёмкости фарад
.
.
Здесь Ф
– – размерность электрической
ёмкости фарад
.
Электрическое поле и его характеристики.
Всякий электрический заряд изменяет свойства окружающего его пространства – создаёт в нём электрическое поле. Об «интенсивности» поля можно судить по воздействию, которое оказывает поле на пробный электрический заряд, помещённый в данную точку пространства.
Силовой характеристикой электрического поля является векторная величина, называемая напряжённостью электрического поля в данной точке пространства, которая численно равна силе, действующей на единичный точечный заряд, находящийся в данной точке поля:
![]() .
.
Направление
вектора
![]() совпадает с направлением силы, действующей
на положительный заряд.
совпадает с направлением силы, действующей
на положительный заряд.
Используя закон Кулона можно получить формулу для напряжённости поля точечного заряда:
![]() .
.
Единица напряжённости в системе СИ имеет название вольт на метр – В/м
Электрическое
поле можно описать с помощью линий
напряжённости (силовых
линий).
Касательная к силовой линии в каждой
точке совпадает с направлением вектора
![]() .
Густота линий выбирается так, чтобы
число линий, пронизывающих единицу
поверхности, перпендикулярной к линиям
площадки, было равно модулю вектора
.
Густота линий выбирается так, чтобы
число линий, пронизывающих единицу
поверхности, перпендикулярной к линиям
площадки, было равно модулю вектора![]() .
.
Для поля точечного
заряда полное число линий, пересекающих
сферическую поверхность произвольного
радиуса
![]() ,
будет равно произведению густоты линий
на площадь поверхности сферы
,
будет равно произведению густоты линий
на площадь поверхности сферы![]() .
Так как густота линий по условию равна
.
Так как густота линий по условию равна![]() ,
то количество линий численно равно
,
то количество линий численно равно![]() ,
т.е. число линий на любом расстоянии от
заряда будет одним и тем же.
,
т.е. число линий на любом расстоянии от
заряда будет одним и тем же.
Силовые линии нигде не пересекаются. Они могут начинаться или заканчиваться лишь на зарядах либо уходить в бесконечность.
Энергетической характеристикой электрического поля является потенциал, который определяют как отношение потенциальной энергии, которой обладает пробный заряд в данной точке пространства к величине этого заряда:
![]() , где
, где
![]() работа
сил поля по удалению пробного заряда
из данной точки на бесконечность, где
предполагается, что электрическое поле
отсутствует, или в такую точку пространства,
где потенциал принимается равным
нулю, например, на заземлённый проводник.
работа
сил поля по удалению пробного заряда
из данной точки на бесконечность, где
предполагается, что электрическое поле
отсутствует, или в такую точку пространства,
где потенциал принимается равным
нулю, например, на заземлённый проводник.
В системе СИ
потенциал измеряется в вольтах
![]() .
.
Энергия взаимодействия системы зарядов.
Для двух точечных
зарядов q1
и q2
,
находящихся
на расстоянии
![]() друг от друга потенциальная энергия их
взаимодействия равна
друг от друга потенциальная энергия их
взаимодействия равна![]() .
.
Для системы, состоящей из N точечных зарядов q1 , q2, …, qN энергия взаимодействия всех зарядов равна сумме энергий взаимодействия зарядов, взятых попарно:
![]() .
.
Суммирование производится по индексам i и k . Оба индекса пробегают, независимо друг от друга, все значения от 1 до N. Слагаемые, для которых значения индекса i совпадают со значением индекса k, не принимаются во внимание.
потенциал, создаваемый всеми зарядами, кроме qi в точке, где помещается заряд qi.
Принцип суперпозиции полей:
а) Напряжённость поля системы зарядов равна векторной сумме напряжённости полей, которые создавал бы каждый из зарядов системы в отдельности:
![]() ;
;
б) Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности:
![]() .
.
Связь между напряжённостью и потенциалом электрического поля.
Из курса механики
известно, что сила связана с потенциальной
энергией соотношением
![]() .
.
Для заряженной
частицы, находящейся в электростатическом
поле
![]() и
и![]() , т.е.
, т.е.![]() .
Тогда
.
Тогда
![]() или
или
![]()
Для произвольного
направления l
получаем
![]() . Знак минус показывает, что вектор
. Знак минус показывает, что вектор![]() направлен в сторонуубывания
потенциала.
направлен в сторонуубывания
потенциала.
Теперь можно легко получить выражение для потенциала точечного заряда:
![]() .
.
Итак: по известным
значениям
![]() можно найти напряжённость поля в каждой
точке или по заданным значениям
можно найти напряжённость поля в каждой
точке или по заданным значениям![]() в каждой точке найти разность потенциалов
между двумя произвольными точками поля,
т.к. работа, совершаемая силами поля над
зарядомq
при перемещении его из точки 1 в точку
2 , может быть вычислена как
в каждой точке найти разность потенциалов
между двумя произвольными точками поля,
т.к. работа, совершаемая силами поля над
зарядомq
при перемещении его из точки 1 в точку
2 , может быть вычислена как
![]() .
.
Вместе с тем
![]() .
Получаем:
.
Получаем:
![]() .
.
Для обхода по
замкнутому контуру
![]() и получаемтеорему
о циркуляции вектора
и получаемтеорему
о циркуляции вектора
![]() :
:
![]()
циркуляция вектора напряжённости электростатического поля равна нулю. Эта формула справедлива только для электрического поля неподвижных зарядов.
Используя теорему
Стокса можно получить теорему
о циркуляции вектора
![]() в дифференциальном виде:
в дифференциальном виде:
![]() .
.
Силовое поле, обладающее таким свойством, называется потенциальным.
Воображаемую поверхность, все точки которой имеют одинаковый потенциал, называют эквипотенциальной поверхностью. Её уравнение имеет вид:
![]() .
.
Силовые линии в каждой точке пространства направлены по нормали к эквипотенциальной поверхности, проходящей через данную точку.
