
2427
.pdf
2) ассоциативность
|
|
|
|
|
|
|
|
(a b ) |
a b a |
b |
|||||
3) дистрибутивность
a (b c ) a b a c
Из определения векторного произведения следуют такие полезные предложения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) |
если a и b - параллельны, то a |
b 0 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|||||
2) |
sin(a |
b ) |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
||
3) |
пусть |
дан |
|
треугольник ABC, |
|
тогда его площадь |
||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
S ABC |
|
|
|
AB |
AC |
|
|
|
|
|||||||||||
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
i |
j |
|
|
k |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a |
b |
x1 |
|
|
|
y1 |
|
|
z1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x2 |
|
|
|
x2 |
|
|
x2 |
|
|
|
|
|
|
|
|
|||
Следствия:
Следствие 1: Для того, чтобы два вектора были коллинеарными необходимо и достаточно, чтобы их соответственные координаты были пропорциональны.
Следствие 2: Рассмотрим ABC , координаты вершин
которого A(x1 , y1 , z1 ) , B(x2 , y2 , z2 ) , C(x3 , y3 , z3 ) . Его площадь
|
|
1 |
|
|
|
i |
|
|
|
j |
|
|
|
k |
|
|
|
|
S |
|
|
x |
|
x |
y |
|
|
|
y |
z |
|
z |
. |
|
|
||
ABC |
|
2 |
2 |
|
2 |
|||||||||||||
|
2 |
|
|
1 |
|
|
1 |
|
1 |
|
|
|
||||||
|
|
|
x |
3 |
x |
y |
3 |
|
y |
z |
3 |
z |
|
|
|
|||
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|||||
|
Определение: Смешенным произведением трех |
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
векторов a , b , |
|
|
(взятых в указанном порядке), |
|||||||||||||||
c |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||
называется |
|
скалярное |
произведение вектора a b на |
|||||||||||||||
вектор c . Абсолютная величина смененного произведения

– объем параллелепипеда, построенного на векторах a , b , c .
Если построить тетраэдр на 3-х векторах a , b , c , его
объем будет равен V |
1 |
S * h , где S - площадь основания |
|
||
|
3 |
|
тетраэдра. Но т.к. площадь треугольника, построенного на
векторах a и b , равна половине площади параллелограмма, построенного на этих же векторах, то
V |
1 |
|
|
1 |
S |
|
|
|
|
|
h |
1 |
V |
|
. Следовательно, |
|
|
|
|
|
|
|
|
|
|
||||||||
тетр |
3 |
2 |
|
парал |
ма |
|
6 |
|
пал да |
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
V |
|
|
(a |
b ) |
c |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||
тетр |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Плоскость.
В аналитической геометрии всякую поверхность рассматривают как геометрическое место точек,
обладающих |
свойством, общим для всех точек |
||||||
F x, y, z |
0 . |
Уравнение плоскости в векторной форме |
|||||
имеет вид z * n = p. |
|
|
|
|
|
||
Здесь |
r x |
i |
y j |
z k радиус-вектор |
текущей |
||
точки |
М |
|
(x; |
|
у; |
z) |
плоскости; |
n i cos |
j |
cos |
k |
cos |
- |
единичный вектор, |
|
имеющий направление перпендикуляра, опущенного на
плоскость из начала координат, |
, |
, углы, образо- |
|
ванные этим |
перпендикуляром |
с |
осями координат |
Ox,Oy,Oz ; р |
— длина этого |
перпендикуляра. При |
|
переходе к координатам это уравнение принимает вид x  cos
cos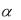 y
y  cos
cos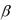 z
z  cos
cos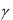 0 (1)
0 (1)

(нормальное уравнение плоскости)
Рассмотрим произвольную плоскость в декартовой прямоугольной системе координат. Введем
т. M 0 x0 , y0 , z0 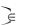 и произвольный ненулевой вектор n , перпендикулярный плоскости . n
и произвольный ненулевой вектор n , перпендикулярный плоскости . n 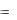 A, B,C , где А,В,С –
A, B,C , где А,В,С –
проекции вектора n на координатные оси. Возьмем какую-
либо точку M x, y, z |
. Построим вектор |
|||||
MM 0 |
x x0 , y |
y0 , z |
z0 |
. Т.к. и т. М и т. М0 принадлежат |
||
|
|
|
|
|||
плоскости |
, а n перпендикулярен , то произведение |
|||||
векторов равно нулю, то есть |
||||||
A(x |
x0 ) |
B y |
y0 |
C z |
z0 0 . Получили уравнение |
|
плоскости, проходящей через заданную точку, перпендикулярно заданному вектору. Каждый ненулевой
вектор перпендикулярный к плоскости |
называется |
||||
нормальным. Раскроем в уравнении скобки и приведем |
|||||
подобные слагаемые Ax |
By |
Cz Ax0 |
By0 Cz0 0 |
||
Обозначим |
Ax0 |
By0 |
Cz0 |
D , тогда |
|
Ax By Cz D 0 |
|
|
|
(2) |
|
если A2 B2 |
C2 |
0 (общее уравнение). |
|
||
Докажем, что в декартовой прямоугольной системе координат каждое уравнение первой степени определяет
плоскость в пространстве: |
Ax |
By |
Cz |
D |
0. |
||
Пусть x0 , y0 , z0 |
какое-нибудь из решений исходного |
||||||
уравнения, |
тогда |
получим |
|
Ax0 |
By0 |
Cz0 D 0 . |
|
Запишем |
|
разность |
|
|
уравнений |
||
A(x x0 ) |
B y y0 |
C z |
z0 |
D |
0 . |
|
Последнее |
уравнение является уравнением плоскости, проходящей
через т. M 0 |
x0 , y0 , z0 и имеющей нормальный вектор |
||||
|
|
|
|
|
|
|
n A, B,C . |
Последнее |
уравнение |
равносильно |
|
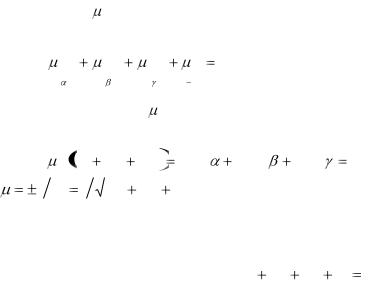
исходному, следовательно, любое уравнение первой степени действительно определяет плоскость в пространстве.
Так как уравнения (1) и (2) описывают одну и ту же плоскость, то их коэффициенты пропорциональны, а это означает, что, умножив обе части уравнения (2) на общий множитель , получим уравнение, совпадающее с
уравнением (1).
Ax |
B y |
C z |
D 0 |
|
|
|
|
cos |
cos |
cos |
p |
Чтобы найти |
|
возведем обе части трех первых |
|
равенств в квадрат и сложим почленно:
2 |
A2 |
B 2 |
C 2 |
cos2 cos2 |
cos2 1, тогда |
|
|
|
|
|
|
|
|
1 N |
1 |
A2 |
B2 |
C 2 , |
(3) |
|
где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.
3) Частные случаи расположения плоскости, определяемой общим уравнением Ax By Cz D 0 А = 0, параллельна оси Ох;
В = 0, |
» |
» |
Оу; |
С = 0, |
» |
» |
Оz; |
D = 0; проходит через начало координат;
А = B = 0; перпендикулярна оси Оz (параллельна
плоскости хОу); |
|
|
|
|
|
|
А = С = 0, » |
» Оу ( » |
» |
хОz); |
|||
В = С = 0, » |
» Ох ( » |
» |
уОz); |
|||
А = D = 0, проходит через ось Ох; |
|
|||||
В = D = 0, |
» |
» |
» |
Оу; |
|
|
С = D = 0, |
» |
» |
» |
Оz; |
|
|
А = В = D = 0; совпадает с плоскостью хОу (z = 0);

А = С = D = 0; » |
» |
» хОz (y = 0); |
|
|||||||||||
В = С = D = 0; » » » |
уОz (х = 0). |
|
||||||||||||
|
|
|
Если в |
общем уравнении |
плоскости |
коэффициент |
||||||||
|
D |
0 , |
|
то, |
разделив |
все |
члены уравнения на - D, |
|||||||
уравнение плоскости можно привести к виду |
||||||||||||||
|
x |
|
y |
|
z |
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
c |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
(здесь |
a |
D A, |
b |
D B , c |
D C ). |
Это уравнение |
||||||||
называется уравнением плоскости в отрезках: в нем а, b и
с - соответственно абсцисса, ордината и аппликата точек пересечения плоскости с осями Ох, Оу и Оz.
Углом между плоскостями A1 x B1 y C1 z D 0 и
A2 x B2 y C2 z D2 0 будем называть любой из
смежных двугранных углов, образованных этими плоскостями (в случае параллельности плоскостей угол считается равным 0 или 180 градусам). Один из двугранных углов равен углу между нормалями как углы с соответственно перпендикулярными сторонами. Косинус угла определяется по формуле
cos |
|
|
|
|
A1 A2 |
B1 B2 |
C1C2 |
|
|
(5) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
A2 |
B 2 |
C 2 |
A2 |
B 2 |
C 2 |
||||
|
|
|
|
|
|
1 |
1 |
1 |
|
2 |
2 |
2 |
|
|
|
Условие параллельности плоскостей; |
|||||||||||||||
|
A1 |
|
B1 |
|
|
C1 |
|
|
|
|
|
(6) |
|||
|
A2 |
B2 |
|
C2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
Условие перпендикулярности плоскостей: |
|||||||||||||||
|
A1 A2 |
B1 B2 |
C1C2 |
0 |
|
|
(7) |
||||||||
|
|
|
Найдем угол между плоскостями |
||||||||||||
5x 15y 35z 3 0,
2x 6 y 14z 1 0

|
n1 |
|
5; 15;35 |
|
|
n2 |
|
2; 6;14 , следовательно, |
|||||
cos |
|
|
5 2 |
15 6 |
|
35 14 |
|
|
1 . |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
4 |
36 |
196 |
25 |
225 |
196 |
|
|||||||
Ответ: 0, 180.
Пусть M* точка пространства, обозначим через d расстояние до плоскости . Назовем отклонением т. M* от 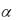 числом = +d, если т. M* лежит по ту же сторону от плоскости, куда идет положительное направление нормали
числом = +d, если т. M* лежит по ту же сторону от плоскости, куда идет положительное направление нормали
и = –d, когда M* лежит с другой стороны от |
. Другими |
||||||||
словами, |
= +d, когда M* и О лежат по разные стороны |
||||||||
от |
и |
= –d, когда они лежат по одну сторону от |
|||||||
плоскости. Для точек плоскости отклонение равно нулю. |
|
||||||||
|
Если |
M * x*, y*, z * |
, |
а |
плоскость |
|
задается |
||
уравнением |
x cos |
y cos |
|
z cos |
p |
0 , |
то |
||
отклонение |
т. М* от |
|
этой |
плоскости |
определяется |
||||
уравнением |
x * cos |
|
y * cos |
z cos* |
|
p |
|
||
Доказательство. Спроектируем т. М* на нормаль Пусть Q – ее
проекция, тогда = OQ – OP, где PQ, OP, PQ – величины направляющих отрезков.
|
|
|
|
|
|
|
|
|
|
|
|
PQ = пр |
|
|
OM * и OP |
p , следовательно, |
|||||||
n |
|||||||||||
|
|
|
|
|
|
||||||
= пр |
|
OM * - p. |
(*) |
||||||||
n |
|||||||||||
Но с другой стороны ОМ* на n это пр n OM * = OM  n =
n =
x * cos
cos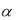 y *
y * cos
cos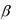 z *
z * cos
cos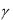 (**)
(**)
Из (*) и (**) следует утверждение теоремы.
Правило. Чтобы вычислить отклонение какой-либо точки М* от плоскости нужно в левую часть нормального уравнения плоскости вместо текущих координат x, y, z подставить координаты очки М*. Полученное число будет равно искомому отклонению. Если требуется найти

расстояние d от т. М* до плоскости, воспользуемся формулой
|
|
|
d |
|
|
|
x * cos |
|
y * cos |
|
|
z * cos |
|
|
|
||||||||||||||||||||||
|
|
Пример: Найти расстояние от точки М(1,3,1) до |
|||||||||||||||||||||||||||||||||||
плоскости3x-4y+12z+14=0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Приведем уравнение плоскости к нормальному виду |
|||||||||||||||||||||||||||||||||||
и найдем . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
3x-4y+12z+14=0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
A, B,C |
|
|
3, |
|
4,12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
, знак |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
A2 |
B 2 |
C 2 |
|
|
|
|
|
9 |
16 |
|
144 |
13 |
||||||||||||||||
берем противоположный знаку D. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Получим |
3 |
|
x |
4 |
|
y |
|
12 |
z |
14 |
0 - нормальное |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
13 |
|
|
|
13 |
|
13 |
|
|
|
|
|
||||||||||||
уравнение. Воспользовавшись теоремой, найдем |
|||||||||||||||||||||||||||||||||||||
отклонение т. М от плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
3 |
|
|
|
4 |
|
3 |
|
12 |
1 |
14 |
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
13 |
|
|
13 |
|
13 |
13 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
d |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Расстояние от точки M 0 |
|
x0 , y0 , z0 |
|
до плоскости, |
|||||||||||||||||||||||||||||||||
определяемой уравнением Ax |
|
|
By |
|
Cz |
D |
0, находится |
||||||||||||||||||||||||||||||
по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
d |
|
Ax0 |
By0 |
|
Cz |
0 |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A2 B2 C 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости; знак результата этой подстановки характеризует взаимное расположение точки и начала координат относительно данной плоскости: «плюс», если

точка М0 и начало координат расположены по разные стороны от плоскости, н «минус», если они расположены по одну сторону от плоскости.
При произвольных значениях А, В и С последнее уравнение определяет некоторую плоскость, принадлежащую связке плоскостей, проходящих через точку М0. Его поэтому часто называют уравнением связки плоскостей.
Уравнение
A1 x B1 y C1 z D |
A2 x B2 y C2 z D 0 (10) |
при произвольном значении 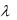 определяет некоторую плоскость, проходящую через прямую пересечения плоскостей
определяет некоторую плоскость, проходящую через прямую пересечения плоскостей
A1 x B1 y C1 z D1 |
0 и |
|
A2 x B2 y C2 z D2 |
0 |
(9.1) |
то есть некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую (в силу чего такое уравнение часто называют уравнением пучка плоскостей). Если плоскости, определяемые уравнениями (9.1), параллельны, то пучок плоскостей превращается в совокупность плоскостей, параллельных этим плоскостям.
Уравнение плоскости, проходящей через три
заданные |
точки |
M1(r1), |
M2(r2), |
M3(r3) |
(здесь |
|||
r1 x1i y1 j z1k , r2 |
x2i y2 j z2 k , r3 |
x3i y3 j z3 k ), |
||||||
проще найти |
из |
условия |
компланарности |
векторов |
||||
r r1 , r2 |
r1 , r3 |
r1 , |
где |
r |
xi |
yj zk - |
радиус-вектор |
|
текущей точки искомой плоскости М: |
|
|
||||||
|
|
(r r1 ) (r2 |
r1 ) (r3 |
r1 ) 0 |
|
|
||
или в координатной форме |
|
|
|
|
|
|||

x |
x1 |
y |
y1 |
z |
z1 |
|
x2 |
x1 |
y2 |
y1 |
z2 |
z1 |
0 |
x3 |
x1 |
y3 |
y1 |
z3 |
z1 |
|
Прямая.
Прямая может быть задана уравнениями двух плоскостей
A1 x B1 y C1 z D1 |
0 |
A2 x B2 y C2 z D2 |
0 |
пересекающихся по этой прямой.
Исключив поочередно х и у из предыдущих уравнений, получим уравнения x az c и y bz d . Здесь прямая определена двумя плоскостями, проецирующими ее на
плоскости хОz и уОz. |
|
|
|
|
|
|
|||||||||||
Уравнения |
прямой, |
проходящей через |
две |
точки |
|||||||||||||
M1 x1 , y1 , z1 |
и M 2 |
x2 , y2 , z2 , имеют вид |
|
|
|
||||||||||||
|
x |
x1 |
|
|
y |
y1 |
|
|
z |
z1 |
|
|
|
|
|
||
|
x2 |
x1 |
|
|
y2 |
|
y1 |
|
|
z2 |
z1 |
|
|
|
|
||
Так называемые канонические уравнения |
|
|
|
||||||||||||||
|
x |
x1 |
|
y |
y1 |
|
z |
z1 |
|
|
|
|
|
|
|||
|
l |
|
|
|
|
m |
|
|
|
|
n |
|
|
|
|
|
|
определяют |
|
прямую, |
проходящую |
через |
точку |
||||||||||||
M1 x1 , y1 , z1 |
и параллельную вектору |
s |
li mj |
nk . В |
|||||||||||||
частности, эти |
уравнения |
могут быть |
записаны |
в виде |
|||||||||||||
|
x |
x1 |
|
y |
y1 |
|
z |
z1 |
, |
|
|
|
|
|
|||
|
cos |
|
|
|
cos |
|
|
|
cos |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
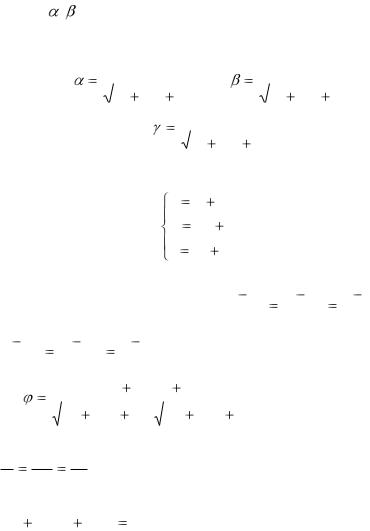
где , ,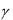 углы, образованные прямой с осями
углы, образованные прямой с осями
координат. Направляющие косинусы прямой находятся по формулам
cos |
|
l |
cos |
|
|
|
m |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
l 2 m2 n2 |
l 2 m2 n2 |
|
||||||||||
|
|
|
|
|
||||||||
|
|
cos |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 2 |
m2 n 2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям:
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
lt |
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
mt |
|
y1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
nt |
z1 |
|
|
|
|
|
|
|
|
|
|
Угол |
|
между |
|
двумя |
|
прямыми, |
|
заданными |
|
их |
|||||||||||||||
каноническими |
|
уравнениями |
|
x |
x1 |
|
y y1 |
|
z |
z1 |
и |
||||||||||||||
|
|
|
l1 |
|
m1 |
n1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x x2 |
|
|
y |
y2 |
|
|
z z2 |
|
определяется по формуле |
|
|
|
||||||||||||
|
l2 |
|
|
|
|
m2 |
|
n2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
cos |
|
|
|
|
l1l2 |
m1m2 |
|
n1n2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
l |
2 m |
2 |
n 2 |
|
l |
2 |
m |
2 |
|
n 2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
1 |
1 |
|
|
|
2 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||
условие параллельности двух прямых: l1 m1 n1
l2 m2 n2
условие перпендикулярности двух прямых:
l1l2 m1m2 n1n2 0
Необходимое и достаточное условие нахождения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):
