2305

Геометрически общее решение представляет собой однопараметрического семейство прямых y Cx C1 , а

особый интеграл параболу.

Рис.4

Непосредственно из чертежа видно, что особый интеграл (парабола) оказался геометрически огибающей семейства интегральных линий (прямых), определяемых общим решением. Это свойство не случайно.

Возможность существования особых решений связана с нарушением условий теоремы Коши. Как мы знаем, выполнение этих условий гарантирует существование и единственность решений – не может быть двух различных решений, удовлетворяющих одному тому же начальному условию. Были рассмотрены случаи, когда эти условия нарушались только в отдельных особых точках. Между тем условия единственности могут нарушаться во всех точках некоторой линии, которая сама может оказаться решением уравнения. Это решение и называют особым.

Пример 6: Уравнение Клеро.

В самом деле, из этих уравнений находим, что

dx ( p)dp ,

dy

откуда p . dx

Подстановка в уравнение Клеро приводит к тождеству

следовательно, не может быть общим интегралом. Он не может быть также получен их общего не при каких значениях С, так как не является линейной функцией. Это так называемый особый интеграл.

2.Дифференциальные уравнения высших порядков

2.1.Основные понятия и определения.

Дифференциальное уравнение n-го порядка можно записать в виде

F(x,y,y',y",...,y(n)) = 0.

(1.1)

Задачей Коши для дифференциального уравнения (1.1) называется задача отыскания решения у=у(х), удовлетворяющего начальным условиям

y(x0 ) y0 , y (x0 ) y10 , y (x0 ) y02 ,..., y(n 1) (x0 ) y0n 1.

(1.2)

Пусть уравнение (1.1) разрешимо относительно старшей производной

y(n) f(x, y, y ,..., y(n 1) ),

(1.3)

тогда для него справедлива теорема существования и единственности решения задачи Коши.

Теорема. Если функция 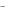в

некоторой области D изменения своих аргументов непрерывна и имеет непрерывные частные производные,

решением этого дифференциального уравнения и для любой задачи Коши с условиями (1.2) найдутся постоянные, определяемые из системы уравнений:

Для уравнения порядка n 2 частное решение может быть задано с помощью условий не в одной точке, а в

то порядок уравнения можно понизить заменой

p f (x, C1 , C2 ,..., Cn k ) , а затем находим y из уравнения y(k ) f (x,C1 ,C2 ,..., Cn k ) k-кратным интегрированием.

Если уравнение не содержит независимого переменного

уравнения на единицу. При этом p рассматривается как новая неизвестная функция от y: p = p(y). Выражаем все

уравнение, получим дифференциальное уравнение (n–1)- го порядка.

Пример 1. Решить уравнение

неинтегрируемый случай.

Следовательно, этот интеграл не выражается в виде конечной комбинации элементарных функций. Однако, если использовать начальные условия, то

1

y 1 x .

Рассмотрим примеры на различные случаи понижения порядка дифференциального уравнения.

Пример 2. Найти общее решение уравнения

Р е ш е н и е. Интегрируя последовательно данное уравнение, имеем

Пример 3. Решить уравнение

y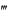1 ( y)2 .

Р е ш е н и е. Данное уравнение не содержит искомой функции y и еѐ производной, поэтому полагаем yp . После этого уравнение примет вид.

Разделяя переменные и интегрируя, получим

Заменяя p через y, получим

Интегрируя последовательно, будем иметь

Пример 4. Решить уравнение

y y 2 2e y .

Р е ш е н и е. Уравнение не содержит независимого

Это есть общий интеграл данного уравнения.

Пример 5. Найти общее решение дифференциального уравнения

xy’’’+y’’=1

Р е ш е н и е. Данное уравнение не содержит y и y’. Положим y’’=z, тогда y

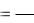
и уравнение примет вид:

x dxdz z 1

Это линейное уравнение первого порядка.

Проинтегрировав это равенство два раза , получим

2.3. Линейные уравнения высших порядков.

Дифференциальное уравнение называется линейным, если неизвестная функция и все ее производные входят в уравнение линейно. Линейное дифференциальное уравнение порядка n имеет вид

y(n) a1 (x)y(n 1) ... a n (x)y f(x) .

Уравнение называется однородным, если f(x) 0, если f(x) 0,то уравнение называется неоднородным. Всякое решение линейного уравнения является частным, особых решений линейное уравнение не имеет.

Линейная комбинация решений однородного линейного уравнения является также решением однородного линейного уравнения. Если известно какоелибо частное решение у1(х) однородного уравнения, то подстановка у(х)=у1(х)z(х) приводит это уравнение к