
2287
.pdf
4.3.2. Квадратичная интерполяция функции одной переменной
Метод Фибоначчи и метод "Золотого сечения" основаны на поиске малого интервала, в котором находится экстремум функции. Это не всегда удобно. Рассмотрим вариант нахождения экстремума, если можно вычислить несколько значений функции в определенных точках и аппроксимировать ее обычным полиномом. Для этого полинома просто вычисляется оптимум, который с достаточной точностью определяет истинный экстремум.
Если существует функция f(x) и известны значения этой функции в трех точках x1, x2, x3, равные соответственно f1, f2, f3, то функция f(x) может быть аппроксимирована квадратичной функцией:
Y (x) Ax 2 Bx C , (4.30)
где А, В, С - постоянные коэффициенты, которые могут быть определены по уравнениям:
Ax12 |
Bx1 |
C |
f1 |
(4.31) |
Ax22 |
Bx2 |
C |
f2 |
(4.32) |
Ax32 |
Bx3 |
C |
f3 |
(4.33) |
Преобразовав уравнение (4.31) - (4.33) можно записать систему уравнений для определения коэффициентов:
A |
(x3 |
x2 ) f1 |
(x1 |
|
x3 ) f 2 |
(x2 |
x1 ) f3 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
(x1 |
|
x2 )(x2 |
x3 )(x3 |
x1 ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
(x |
2 |
x 2 ) f |
1 |
|
(x 2 |
|
x |
2 ) f |
2 |
(x |
2 |
x 2 ) f |
3 |
|
|
|
|
|
|
|||||||
B |
|
2 |
3 |
|
|
|
3 |
|
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
(x1 |
|
x2 )(x2 |
|
x3 )(x3 |
x1 ) |
|
|
|
|
|
|
|
|
|
|
(4.34) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
C |
x2 x3 (x3 |
x2 ) f1 |
|
x1 x3 (x1 |
x3 ) f 2 |
|
|
x1 x2 (x2 |
x1 ) f 3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
(x1 |
|
x2 )(x2 |
x3 )(x3 |
|
|
x1 ) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение задачи поиска оптимума функции (4.30) достаточно просто. Для |
|||||||||||||||||||||||||||
этого необходимо решить уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Y (x) 2Ax |
B |
0 . |
|
|
|
|
|
|
|
(4.35) |
|||||||||
Его решением является значение x4, которое с учетом (4.34) можно запи- |
|||||||||||||||||||||||||||
сать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
1 |
|
|
(x |
2 |
x |
2 ) f |
1 |
(x 2 |
|
x 2 ) f |
2 |
|
(x 2 |
x 2 ) f |
3 |
|
|
|
|||||
x4 |
|
|
|
|
|
|
|
|
2 |
3 |
|
3 |
|
1 |
|
|
|
1 |
2 |
. |
(4.36) |
||||||
|
|
2A 2 (x2 |
x3 ) f1 |
(x3 |
|
x1 ) f 2 |
(x1 |
x2 ) f3 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
Следует заметить, что если точность определения оптимума функции Е задана достаточно малой, то значения x1, x2, x3 и f1, f2, f3 будут достаточно близки друг к другу и значение x4 (4.36) может стать вообще недостижимым. Поэтому при проведении всех последующих интерполяций (после первой) для определения значения x4 предлагается использовать выражение:
x |
|
x1 x2 |
|
( f1 |
f 2 )(x2 |
x3 )(x3 |
x1 ) |
|
(4.37) |
4 |
2 |
|
2 (x2 x3 ) f1 |
(x3 |
x1 ) f 2 |
(x1 x2 ) f |
|
||
|
|
|
3 |
|

При решении задачи поиска минимума функции f(x) методом квадратичной интерполяции вычислительные процедуры производятся в следующей последовательности. Исходными условиями для решения задачи является начальная аппроксимация x1, истинного оптимума xэкс и величина шага аппроксимации h (рис. 4.11) .При этом необходимо следить за тем, чтобы величина h и расстояние от x1 до xэкс были величинами одного порядка.
h
хэкс |
х |
1 |
х1+h=x2 |
|
|
|
Рис.4.11. Начальные условия задачи поиска оптимума методом квадратичной интерполяции.
Точка, полученная из x1 путем ее увеличения на h, является точкой x2 из выражения (4.36). В этих точках x1 и x2 вычисляется значение функции f(x1) и f(x2). При этом может возникнуть ситуация f(x1) > f(x2) (рис. 4.12, а) или f(x1) < f(x2) (рис. 4.12, б). Если выполняется первое неравенство, то в качестве точки x3 выбираем точку с координатами x1 + 2h (рис. 4.12,а) и вычисляем значение функции в этой точке. Если же выполняется второе неравенство, то в качестве точки x3 принимаем точку с координатами x1 - h (рис. 4.12, б) и вычисляем значение функции в этой точке. Однако может возникнуть ситуация при которой полученные результаты вычислений не соответствуют представленным на рис.4.12, т.е. если выполняется неравенство:
f (x3 ) f (x1 ) f (x2 ) |
при |
x3 |
x1 |
x2 |
|
|
f (x3 ) f (x2 ) f (x1 ) |
|
x3 |
|
|
, |
(4.38) |
при |
x |
2 |
x1 |
|
||
которые представлены на рис.(4.13, а и б) соответственно. О порядке решения таких задач будет сказано ниже.
На следующем этапе по выражению (4.36) определяется значение точки x4 и вычисляется функция в этой точке f(x4). После этого производится сравнение всех полученных значений функций f(x1)…f(x4) и выбираются два наименьших. Если разница между ними меньше заданной точности вычислений:
f (xi ) f (xk ) |
E , |
(4.39) |
то считаем, что задача решена и найден корень (т.е. точка минимума) с требуемой точностью.
Если условие (4.39) не выполняется, то отрабатывается точка с наибольшим значением функции f(x) и происходит новое определение четвертой точки, только уже по выражению (4.37). Этот процесс повторяется до тех пор, пока условие (4.39) не будет выполнено.

f(х3)
f(х1)
f(х2)
h h
х1 |
х2 |
х3 |
a
f(х2)
f(х3)
f(х1)
h h
х3 |
х1 |
х2 |
б
Рис.4.12. Выбор третьей точки при решении задачи методом квадратичной интерполяции.
|
|
f(х1) |
f(х2) |
||
f(х3) |
|
|
|||
|
|
|
|
||
|
h |
|
|
h |
|
|
|
|
|
|
|
х3 |
х1 |
х2 |
|||
a
f(х1)
f(х2)
f(х3)
h h
х1 |
х2 |
х3 |
б
Рис.4.13 Пример неудачного расположения значения f(x3).

Если при выполнении вычислений значение функций удовлетворяют условию (4.38), то отбрасывается точка, не валяющая на границы интервала, в котором расположен экстремум. Например, для случая, изображенного на рис.4.14, отбрасывается точка x1.
f(х1)
f(х2)
f(х4)
f(х3)
х1 |
х2 |
х3 |
х4 |
Рис.4.14. Выбор интервала с экстремумом функции.
Изложенный выше порядок поиска минимума функции методом квадратичной интерполяции может быть реализован с помощью алгоритма, представленного на рис.4.15
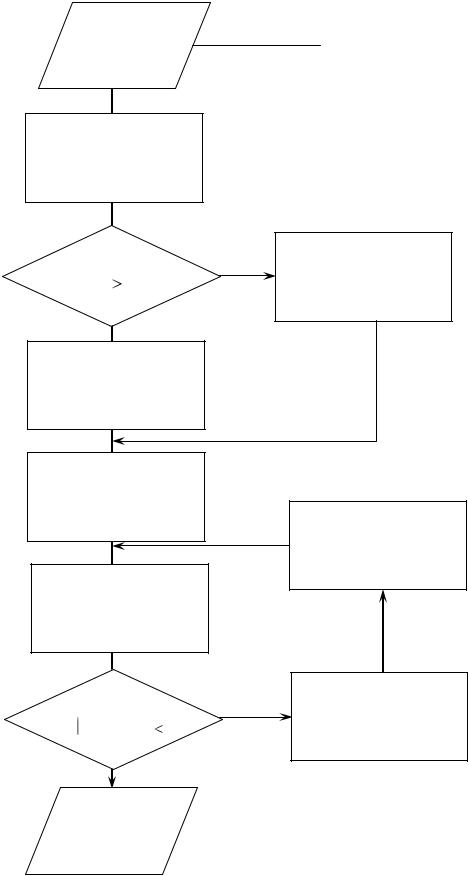
Если методом квадратичной интерполяции ищется максимум функции, то решение задачи происходит точно в такой последовательности, только изменяются неравенства при нахождении точки x3 и условия выбора интервала, в случае если возникла ситуация, аналогичная представленной на рис.4.13. Алгоритм поиска максимума функции методом квадратичной интерполяции представлен на рис 4.16.
4.3.3. Кубическая интерполяция функции
Рассмотренный выше метод квадратичной интерполяции функции позволяет аппроксимировать исследуемую функцию квадратичным трехчленом. Ниже излагается метод, широко применяемый при линейном поиске оптимума, который аппроксимирует функцию кубическим полиномом. Этот метод позволяет достигнуть большей точности при поиске оптимума, чем метод квадратичной интерполяции.
Если существует функция f(x1, x2,... xn), проходящая через точку x0 с координатами (x01, x02,...x0n), то ее можно минимизировать (максимизировать) на прямой X0 + hd, где h - это шаг некоторой длины, а d - это некоторое направление. Функцию f(x1, x2 ...xn) можно представить в виде:
|
|
Y (h) |
f ( X 0 hd) |
f (x01 |
hd1 ; x02 |
hd2 ;...x0n |
hdn ) . |
(4.40) |
|||||
Производная функции (4.40) выглядит следующим образом: |
|
||||||||||||
|
dY |
|
df |
|
( X 0 hd)d1 |
df |
( X 0 |
hd)d 2 |
|
df |
( X 0 |
hd)d n |
(4.41) |
|
|
|
dx1 |
|
|
||||||||
|
dh |
|
|
dx2 |
|
|
dxn |
|
|
||||
или

Ввод на- |
Начальное значение Х1 |
|
чальных |
Шаг h |
|
Точность Е |
||
данных |
||
|
||
|
|
Вычисление f(x1); x2=x1+h; f(x2)
Если f(x1) f(x2)
Вычисление х3=х1+2h; f(x3)
Вычисление х4; f(x4)
Выбор двух наименьших значений f(xi) и f(xk)
Вычисление х3=х1-h; f(x3)
Вычисление х4 и f(x4)
Если |
Выбор новых то- |
|
чек х1, х2, x3 |
||
f(xi)-f(xk) E |
||
|
||
|
|
Вывод результата
Рис. 4.15. Алгоритм поиска минимума функции методом квадратичной интерполяции
Ввод на- |
Начальное значение Х1 |
|
чальных |
Шаг h |
|
Точность Е |
||
данных |
||
|
||
|
|
Вычисление f(x1); x2=x1+h; f(x2)
Если f(x1) f(x2)
Вычисление х3=х1+2h; f(x3)
Вычисление х4; f(x4)
Выбор двух наименьших значений f(xi) и f(xk)
Если
f(xi)-f(xk)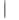 E
E
Вывод результата
Вычисление х3=х1-h; f(x3)
Вычисление х4 и f(x4)
Выбор новых точек х1, х2, x3
Рис. 4.16. Алгоритм поиска максимума функции методом квадратичной интерполяции.

dY |
grad X 0 hd T d |
(4.42) |
|
dh |
|||
|
|
Для решения задачи поиска экстремума необходимо знать значение функции (4.40) и ее производной (4.42) в двух точках А и В:
Y(A) = Ya; Y'(A) = Ya
Y(B) = Yb; Y'(B) = Yb. (4.43)
Если эти условия выполняются, то функция Y(h) может быть аппроксимирована кубическим полиномом вида:
Z (h) |
h h 2 |
h3 , |
(4.44) |
где 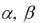

 - коэффициенты полинома, которые можно получить из системы уравнений, при этом полагаем, что A = 0:
- коэффициенты полинома, которые можно получить из системы уравнений, при этом полагаем, что A = 0:
ya
B B 2 B 3 y |
b |
|
|
Ya |
(4.45) |
|
2 B 3 B 2 YB
Система (4.45) имеет следующее решение:
ya ; |
Ya ; |
Ya |
C |
; |
Ya |
Yb |
2C |
|
|
|
|
|
|
(4.46) |
|||
|
B |
|
3B2 |
|
||||
|
|
|
|
|
|
|
||
где С - коэффициент, определяемый как:
C |
3 ya |
yb |
Ya |
Yb . |
(4.47) |
|
B |
||||
|
|
|
|
|
Подставив в выражение (4.44) значения коэффициентов (4.46) и (4.47) можно решать классическую задачу поиска оптимума функции. Первая производная и уравнение, которое необходимо решить для нахождения точек перегиба выглядит следующим образом:
Ya 2 Ya C |
h |
Ya |
Yb |
2C |
h2 |
0 |
, |
(4.48) |
|
B |
B2 |
||||||||
|
|
|
|
|
|
|
где С - коэффициент, определяемый по (4.47). Решением этого уравнения являются два корня
R1,2 |
Ya |
C |
B |
(4.49) |
|
Ya |
Yb 2C |
||||
|
|
|
где - коэффициент, знак которого влияет на характер экстремума функции; он определяется по выражению:
C 2 Ya Yb . |
(4.50) |
Если в выражении (4.49) выбрать знак "+", то вторая производная функ-
ции z(h) (4.44):

z (h) |
2 |
Ya C |
2 |
Ya Yb 2C h , |
(4.51) |
|
B |
B 2 |
|||||
|
|
|
|
если предположить, что соотношение h/B равно:
|
|
|
|
|
|
|
|
h |
|
|
Ya |
|
C |
|
|
|
, |
|
|
|
|
(4.52) |
||
|
|
|
|
|
|
|
|
B |
|
|
Y |
|
|
Y |
|
2C |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
то вторая производная (4.51) примет вид: |
|
|
|
|
|
|
|
|
|
|||||||||||||||
z (h) |
2 |
Ya |
C |
|
2 |
|
Ya |
Yb |
|
2C |
Ya |
C |
B |
|||||||||||
B |
|
B 2 |
|
Y |
a |
Y 2C |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
(4.53) |
|
|
2Ya |
|
|
2C 2Ya |
|
|
2C 2 |
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0 |
|
|
|
||||||||||||||
|
B |
|
|
|
B |
|
B |
|
|
B |
|
B |
|
|
B |
|
|
|
||||||
Т.е. вторая производная положительна, а в точке R1, определяемой по (4.49) наблюдается минимум функции. Аналогичные результаты можно получить для точки Rz, в которой вторая производная отрицательна: z"(h) = -2 /B < 0. Т.о. для определения точек минимума и максимума функции R1, R2 предлагается использовать следующие выражения:
R1 min |
|
Ya |
C |
|
|
B |
(4.54) |
Ya |
Yb |
|
|
||||
|
2C |
|
|||||
|
|
|
и |
|
|
|
|
R2 max |
|
Ya |
C |
|
|
B |
(4.55) |
|
Ya |
Yb |
|
|
|||
|
|
2C |
|
||||
При практическом применении метода для определения точек минимума и максимума рекомендуется использовать выражение:
Rmin |
C |
|
Ya |
B |
(4.56) |
|
Yb |
Ya |
2 |
||||
|
|
|
||||
|
|
и |
|
|
|
|
Rmax |
C |
|
Ya |
B |
(4.57) |
|
Yb |
Ya |
2 |
||||
|
|
|
Выбор точки В является задачей пользователя и зависит от характера определяемого экстремума. Если ищется минимум, то могут возникнуть следующие варианты:
1)Градиент функции y(h) отрицательный Ya < 0, т.е. функция убывающая
инеобходимо выбрать B > 0 для того чтобы двигаться в направлении убывания;
2)Градиент функции (4.40) положительный, т.е. Ya > 0. В этом случае необходимо выбрать B < 0.
Если осуществляется поиск максимума функции, то:
3)В случае Ya < 0 выбираем B < 0;
4)В случае Ya > 0 выбираем B > 0.
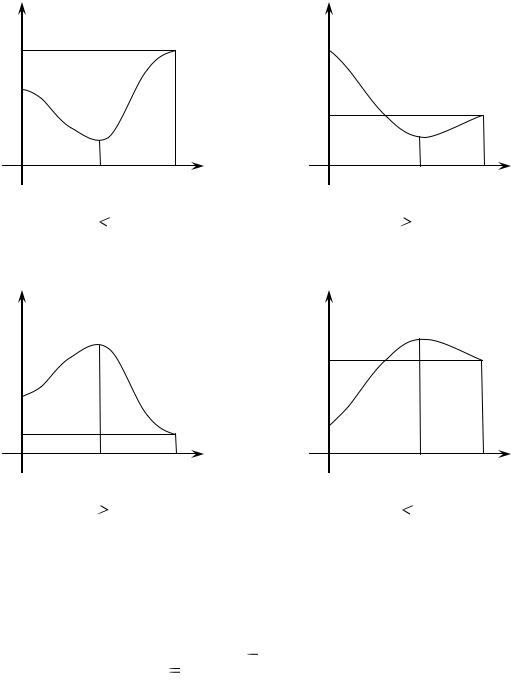
Вторая точка В должна быть выбрана таким образом, чтобы интервал (0; В), а мы договорились, что А = 0; содержал точку экстремума (рис. 4.17). В случае когда условия, приведенные на рис. 4.17 не выполняются, значение интервала (0; В) увеличивается в два раза и вновь исследуется на наличие в нем точек экстремума. Если их опять нет, то процесс увеличения интервала продолжается сколь необходимо долго.
y(h) |
|
|
|
|
y(h) |
|
|
|
|
y(B) |
|
|
|
|
y(A) |
|
|
|
|
y(A) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(B) |
|
|
|
|
0 |
Rmin |
|
B |
h |
0 |
Rmin |
B |
h |
|
|
y(A) |
y(B) |
|
|
|
YA |
0 |
|
|
|
|
|
|
|
a |
|
|
|
|
y(h) |
|
|
|
|
y(h) |
|
|
|
|
|
|
|
|
|
y(B) |
|
|
|
|
y(A) |
|
|
|
|
|
|
|
|
|
y(B) |
|
|
|
|
y(A) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Rmax |
B |
h |
0 |
Rmax |
B |
h |
||
|
y(A) |
y(B) |
|
|
|
YA |
0 |
|
|
|
|
|
|
|
б |
|
|
|
|
Рис. 4.17. Условия расположения точки экстремума в интервале при поиске минимума (а) и максимума (б) функции.
Начальное значение В рекомендуется определять по выражению:
B |
2 |
y( A) f min(max) |
|
|
||
|
|
, |
(4.58) |
|||
Ya |
||||||
|
|
|||||
|
|
|
|
|||
где fmin(max) - предполагаемое значение истинного минимума функции.
Общий ход решения задачи поиска оптимума функции методом кубической интерполяции выглядит следующим образом:

1.Определяем по известному значению А величину y(A) по уравнению (4.40) и градиент функции Ya (4.42).
2.Определяется направление поиска d. Если ищем минимум:
-Ya < 0, то направление "+d"
- Ya 0, то направление "-d". Если ищем максимум:
-Ya < 0, то "-d"
-Ya 0, то "+d".
3.По выражению (4.58) определяется В и выбирается его знак в соответствии с рассуждениями, приведенными выше.
4.Определяется y(В) и Yb.
5.По их значениям, и в соответствии с рис. 4.17, определяем попала ли точка экстремума в наш интервал. Если не попала, то увеличиваем его с В на 2В
ивозвращаемся к предыдущему пункту.
6.По выражениям (4.54) или (4.55) аппроксимируем точки минимума или максимума на полученном интервале.
7.Определяем градиент функции y(h) в точке R:
y'(h) = grad(X0 +rd)Т.d = YR
Если YR < e, т.е. достигнута заданная точность вычисления, то задачу считаем решенной. Если же это условие не выполняется, то возвращаемся к п.6 и проводим аппроксимацию на новом интервале (О; R), если YR > 0 (для минимума) или YR 0 (максимума) и интервал (R; В) если YR 0 (для минимума) или YR > 0 (для максимума).
