2232

Автоматы S и Т называют неотличимыми или эквивалентными, если для любого состояния q автомата S найдется неотличимое от него состояние r автомата Т и, наоборот, для любого состояния r автомата T найдется неотличимое от него состояние q автомата S. Неотличимость автоматов означает, что любое автоматное отображение, реализуемое одним из них, может быть реализовано другим.

Ставится задача: среди автоматов, эквивалентных S, найти автомат с наименьшим числом состояний – минимальный автомат.

Наиболее известным алгоритмом нахождения эквивалентных состояний является алгоритм Мили:

Пусть дан автомат S=(A,Q,V, , ) c n состояниями. На любом шаге алгоритма будем строить некоторое разбиение Q на классы, причем разбиение на следующем шаге будет получаться путем расщепления некоторых классов предыдущего разбиения.

Шаг1: Два состояния q и q' относим в один класс сj, тогда и

одному и тому же классу сi,j. Если (i+1) шаг не изменяет разбиения, то алгоритм заканчивается и полученное разбиение является разбиением на классы эквивалентных состояний.

В нашем примере вычеркиваются строки 4, 8, 7; в клетках полученной таблицы 4 заменяем на 1; 8 на 2; 7 на 5. В результате получим таблицу.

Автомат, заданный представленной таблицей будет эквивалентным данному исходному автомату.

62

5.3. Сети из автоматов

Автомат называется комбинационным, если для каждого входного символа а и любых состояний qi и qj: λ(qi, a)= λ(qj, a), иначе говоря, если выходной символ не зависит от состояния и определяется текущим входным символом. В таком автомате все состояния эквивалентны и, следовательно, минимальный комбинационный автомат имеет одно состояние. Функция переходов в нем вырождена; его поведение однозначно задается функцией выходов с одним аргумен-

том: λ(ai)=Vj.

Автомат называется логическим, если его входной алфавит состоит из 2m двоичных наборов длины m, а выходной из 2n двоичных наборов длины n. Функция выходов логического комбинационного автомата – это просто система n логических функций от m переменных (i-я функция определяет значения i-ой компоненты в выходном векторе автомата).

5.4. Синхронные сети

Если автоматы рассматривать как устройства с входами и выходами, то присоединение выходов одних автоматов ко входам дру-

гих дает схему, или сеть из автоматов.

Под состоянием сети из m одновременно работающих автоматов S1, …, Sm (компонент сети) понимается вектор (qi1, …, qim), где qij

– состояние автомата Sj. Поэтому, в общем случае число возможных состояний сети равно произведению чисел состояний составляющих ее компонент.

Вектор – состояние сети указывает, в каких состояниях находятся компоненты сети в один и тот же момент времени. Следовательно, при описании автоматных сетей, в отличие от абстрактных автоматов, необходимо вводить понятие времени. Существует два способа – синхронный и асинхронный. При синхронном способе вводится шкала времени, которая делится на отрезки одинаковой длины (такты), нумеруемые 0, 1, 2, …. Входное слово рассматривается как слово длины к, занимает к тактов. Его буквы можно считать функциями времени a(t) – буква, появившаяся в момент t. Автоматные функции δ и λ реализуются с задержкой. Время задержки функции равно единице: δ(q(t), a(t))=q(t+1); состояние определяется за-

63

ранее. Время задержки λ обычно считают равным нулю:

δ(q(t),a(t))=V(t).

Рассмотрим некоторые основные виды соединения автоматов:

1. Параллельное соединение.

Рис. 12

а) С раздельными входами и алфавитами А1 и А2 (рис. 12а). Здесь пару автоматов S1 и S2

S1=( A1, Q1, V1, δ1, λ1)

S2=( A2, Q2, V2, δ2, λ2)

можно рассматривать как один автомат S=(A, Q, V, δ, λ), опре-

деленный так: A=A1xA2, Q=Q1·Q2, V=V1·V2,

следовательно, входной символ автомата S – это пара символов а=(а1, а2), состояние S

q=(q1, q2),

δ(q, a)=δ((q1, q2), (а1, а2))= (δ1(q1, q2), δ2(а1, а2)),

т.е. смена состояний происходит независимо и одновременно.

Аналогично

λ(q, a)= (λ 1(q1, q2), λ 2(а1, а2))= (V1, V2).

Автомат S называется прямым произведением автоматов S1 и

S2.

б) С общим входом и алфавитом А (рис. 12б).

Этот автомат определяется аналогично, с той лишь разницей,

что алфавиты А1, А2 и А совпадают, поэтому

δ(q, a)= (δ1(q1, а), δ2(q2, а)) и.т.д.

2. Последовательное соединение.

V1=A2

A1 S1 S2 V2

Рис. 13

64

Эту сеть можно описать как автомат S=(A, Q, V, δ, λ), причем A=A1, V=V2, V1=A2. Как и прежде Q= Q1·Q2. Если задержка λ1 равна нулю: λ 1(q1(t), a(t)) = V1(t), то

q(t+1)=(q1(t+1), q2(t+1)) = (δ1(q1(t), a(t), δ2(q2(t), λ 1(q1(t), a(t)))).

Выражение в правой части зависит только от q(t) = (q1(t), q2(t)) и a(t). Эта функция и есть функция δ для S: q(t+1) = δ(q(t), a(t)). Ее конкретная таблица зависит о таблиц δ1, δ2 и λ.

3. Обратная связь.

ратная связь. Пусть в момент t V=0, тогда x2(t)=0 V(t)= x1 t x2 t =1,

т.е. V(t) равен и нулю и единице в один и тот же момент, т.е. получаем противоречие. Этот пример показывает, что сеть из автоматов, содержащая контур обратной связи без задержек, может не иметь конкретной автоматной интерпретации.

С другой стороны, обратная связь с задержкой оказывается мощным средством построения автоматов. Всякий автомат при син-

ме.

Здесь блок λ – комбинационный автомат с входным алфавитом AxQ и выходным алфавитом V; блок δ – комбинационный автомат с тем же входным алфавитом и выходным Q.

Блок D – блок, задерживающий поступающие на него сигналы на 1 такт. Он представляет собой автомат Мура, входной и выход-

65

ной алфавиты которого совпадают и равны Q={q1, …, qn}, алфавит состояний R={r1, …, rn} имеет ту же мощность, что и Q, λD(ri)=qi,

δD(ri, qj)=rj для всех i, j=1, …, n.

Сеть Петри – математическая модель дискретной динамической системы, в т.ч. и информационной.

Сетью петри называется набор N=(T,P,F,M0), где Т – конечное множество символов, называемых переходами; Р - конечное множество символов, называемых местами; Р Т= ; F – функция инцидентности.

F: T P P T {0;1}, M0 – начальная разметка мест:

M0: Р {0;1;2….}.

Неформально сеть Петри представляют размеченным ориентированным графом со множеством вершин Т Р. Из вершины места р Р, изображаемой кружком ведет дуга в вершину-переход t T, изображаемому прямоугольником, тогда и только тогда, когда

F(p,t)=1

(p - входное место перехода t; на рис 16 P={p1, p2, p3}, T={a, b, c, d}). Из вершины-перехода t ведет дуга в вершину-место р тогда и только тогда, когда

F(p,t)=1

(p - входное место перехода t). Место р помечается разметкой M0(p) 0, часто изображаемой различным числом точек (фишек).

Динамика поведения моделируемой сети описывается в терминах функционирования сети Петри.

P

b P3

1

d

Рис. 16

66

Сеть функционирует в дискретном времени, переходя от разметки к разметке. Конечная разметка – это функция: М: Р {0,1,2,…}; смена разметок происходит в результате срабатывания переходов сети. Переход t T может сработать при разметке М, если для любого р Р:

M(p)-F(p,t) 0,

т.е. если каждое его входное место имеет хотя бы одну фишку. В результате срабатывания t при разметке M последняя сменяется на M' по правилу: для любого р Р

M'(p)= M(p)-F(p,t)+ F(t,p),

т.е. переход t изымает по фишке из каждого своего входного места и посылает по фишке в каждое свое выходное место. Если может срабатывать несколько переходов, то срабатывает один, любой из них. Сеть останавливается, если при некоторой разметке (тупиковая разметка) ни один из ее переходов не может срабатывать. При одной и той же начальной разметке сеть Петри может порождать, в силу недетерминированности ее функционирования, различные последовательности срабатывания ее переходов. Эти последовательности образуют слова в алфавите Т, а множество всевозможных слов, порождаемых сетью Петри, называется ее языком. Две сети Петри эквивалентны, если они порождают один и тот же язык.

5.5. Программная реализация логических функций

Представление автомата схемой элементов – это первый вид структурной реализации автомата. Другой ее вид – это реализация автомата программой.

Ограничимся вопросами программной реализации логических функций. Под программой понимаем пронумерованную последовательность команд к1,…, кS, взятых из фиксированного набора (система команд). Программа работает над конечным множеством проименованных двоичных ячеек. Имя ячейки (адрес), чаще всего – имя логической переменной, значение которой хранится в этой ячейке.

Система команд содержит команды-операторы вида:

1) Одноадресные

67

b:=f(a1,…, ap) (выполнить операцию f над содержимым ячеек a1,…, ap и результат положить в ячейку b)

2)Двухадресные условные переходы двух видов:

1.«если а, то i, иначе j» (если a=1, то выполняем ki, иначе kj);

2.«если не а, то i, иначе j».

Операция f(a1,…, ap) – это логическая функция р-переменных (в частности она может быть константой 1 или 0).

Если j=i+1, то переход можно считать одноадресным: (если а, то i (иначе перейти к ki+1)), а если i=j, то безусловным: «перейти к i». Любая из указанных команд может быть заключительной, что указывается словом «конец».

Процессом вычисления программы к1,…,к3 называется последовательность шагов k(1), k(2),…,k(t), на каждом шаге которой выполняется одна команда программы. Эта последовательность определяется так:

1.k(1)=k1 ;

2.если k(i)=kr-оператор, то k(i+1)=kr+1;

3.если k(i) – нулевой переход, то номер команды k(i+1) указывается этим переходом;

4.если k(i) - заключительная команда, остановка процесса после ее выполнения.

Программа П вычисляет (или реализует) логическую функцию f(x1,…, xn)=y, если для любого двоичного набора =( 1,…, n) при начальном состоянии памяти х1= 1,…, хn= n, (состояние остальных ячеек несущественно), программа через конечное число шагов остановится и при этом в ячейке у лежит величина f=( 1,…, n).

Если под сложностью автомата мы понимаем число элементов в его схеме, то сложность программы можно понимать в различных смыслах (по числу команд, по времени реализации и т.д.)

Любой схеме, реализующей функцию f и содержащей N элементов, нетрудно поставить в соответствие программу, реализующую f и состоящую из N команд, следующим образом: занумеруем элементы схемы числами 1,2,…,n так, чтобы на любом пути от входа к выходу номера элементов возрастали; при этом номер 1 получит один из входных элементов, а номер N – выходной элемент. Пусть элемент ei схемы реализует функцию i и к его входам присоединены выходы элементов ej1,…, ej (некоторые из них могут быть входами схемы). Поставим элементу ei в соответствие либо ячейку аi

68

и команду аi= i(aj1,…, ajp), если i N; либо ячейку у и команду «y:= N(aj1,…, ajp) конец», если i=N. Получим программу без условных переходов (их называют операторными), в которой порядок команд

в точности соответствует нумерации элементов в схеме.

Проблемы синтеза операторных команд сводятся к проблемам синтеза схем: в частности, вопросы функциональной полноты системы команд и минимизации собственного текста операторной программы совпадают с задачами о полноте системы функций и о минимизации схем.

Другой «крайний» вид программ, вычисляющих логические функции – это программы, состоящие из команд вида y:= ( =0 или =1) и условных переходов. Такие программы называют бинарными программами. Всякую булеву формулу F, содержащую N букв, можно реализовать бинарной программой, вычисляющей F за время N и содержащей N команд условного перехода. Для описания метода реализации используем представление программы в виде графа в котором вершины соответствуют командам, а ребра – переходам. Пусть G1 – граф программы для функции f1 с начальной вершиной

V10 и двумя заключительными вершинами V10Z (с командой “y=0”) и

команда «y=0» при этом отбрасывается), вычислит функцию f=f1 f2; 3) программа, граф которой получен из G1 заменой команд

V10Z и V11Z на инверсные(«y:=0» на «у:=1») вычисляет f1.

Отметим, что в графе G получаются две единичные, а в графе G‟ – две нулевые заключительные вершины. В обоих случаях их надо отождествить.

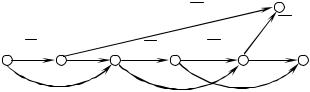
Пример 5.5: Формула (x1 x2) ( x3 x4 x5) реализуется бинарной программой, граф которой имеет вид:

69

Рис. 17

Описанный метод не гарантирует минимальности полученных программ по времени и числу команд.

Вывод: Логический автомат всегда может быть реализован бинарной программой, не требующей промежуточной памяти.

70