2232

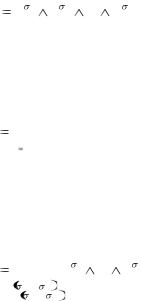
3) Множество M=L замкнуто, так как каждое линейное выражение, составленное из линейных выражений линейно.

1.6. Проблема минимизации булевых функций

Пусть задан алфавит переменных {x1, …, xn}.

Определение: Выражение

называется элементарной конъюнкцией. Число r называется рангом элементарной конъюнкции.

По определению считаем константу 1 элементарной конъюнкцией ранга 0.

Определение: Выражение

s

R V ki (ki≠kj при i≠j),

i 1

где ki – элементарная конъюнкция ранга ri называется дизъюнктивной нормальной формой (д.н.ф.).

Очевидно д.н.ф. R реализует некоторую булеву функцию

f(x1, …, xn).

В качестве реализующей функции f(x1, …, xn) д.н.ф. можно взять, например совершенную д.н.ф.

Пример: Рассмотрим f(x1, x2, x3), заданную таблицей.

Тогда ее можно представить в виде совершенной д.н.ф.

21

R1 = x1 x2 x3 V x1 x2 x3 V x1 x2 x3 V x1x2 x3 V x1x2x3.

С другой стороны, непосредственной проверкой убеждаемся, что эта функция может быть представлена формами

22

Этот пример показывает, что функция алгебры логики определяется с помощью д.н.ф. не единственным образом. Возникает возможность выбора более предпочтительной реализации. Для этого вводится индекс простоты L(R).

Встречаются следующие индексы простоты:

1.LБ(R) – число букв переменных в записи д.н.ф. R LБ(R1)=15; LБ(R2)=7; LБ(R3)=7; LБ(R4)=3.

2.LК(R) – число элементарных конъюнкций, входящих в R LК(R1)=5; LК(R2)=3; LК(R3)=3; LК(R4)=4.

3.LО(R) – число символов отрицания в R

LО(R1)=7; LО(R2)=2; LО(R3)=3; LО(R4)=2.

Так как над алфавитом {x1, …, xn} можно построить 3n различных элементарных конъюнкций, следовательно, число д.н.ф. над

этим алфавитом равно 23n .

Обычно простейшую д.н.ф. относительно LБ(R) называют ми-

нимальной, а относительно LК(R) – кратчайшей.

Задача выбора минимальной д.н.ф. для f(x1, …, xn) может быть

решена тривиальным перебором 23n д.н.ф., но этот путь порочен ввиду громоздкости.

23

1.7. Упрощение д.н.ф. Тупиковые (относительно упрощения) д.н.ф.

Пусть R – произвольная д.н.ф. и R=R' V K; R=R' V xi i K',

где К – некоторая элементарная конъюнкция из R,

R' – д.н.ф., образованная из остальных конъюнкций, xi i - некоторый множитель из К,

К' – произведение остальных сомножителей. Рассматриваются 2 типа преобразований д.н.ф.

1. Операции удаления элементарной конъюнкции.

Переход от д.н.ф. R к д.н.ф. R' – преобразование, осуществляемое путем удаления К. Определена операция тогда и только тогда, когда R'=R.

2. Операции удаления множителя.

Переход от д.н.ф. R к д.н.ф. R'VK' – преобразование, осуществляемое путем удаления xi i . Преобразование осуществляется тогда

и только тогда, когда R'VK'=R.

Определение. Д.Н.Ф. R, которую нельзя упростить при помощи преобразований 1 и 2, называется тупиковой д.н.ф. относительно преобразований 1 и 2.

Нетрудно видеть, что среди тупиковых д.н.ф. функций f(x1, …, xn) всегда содержатся и минимальные, возможно, правда, не все.

Пример. f(x1, x2, x3)

24

= x1 x2 V x2x3 V x1 x3 =R'

x1 x2 x3 V x1 x2 x3 V x1 x2x3 V x1 x2 x3 V x1x2 x3 V x1x2x3 =

=x2 x3 V x1 x3 V x1x2.

2.Язык логики предикатов

2.1. Основные понятия логики предикатов

Определение. Предикатом P(x1, …, xn) называется функция Р:

Mn→B, где М – произвольное множество; B={0, 1} т.е. n-местный предикат – двузначная функция от n аргументов, определенных на множестве М. М – называется предметной областью, x1, …, xn -

предметные переменные.

Поскольку P(x1, …, xn) - это логическая (двоичная) переменная, то из предикатов можно образовывать выражения логики высказываний, т.е. формулы типа

Эта формула может рассматриваться и как составная булева формула, описывающая функцию алгебры логики от трех логических переменных P1(x1, x2), P1(x2, x4), P2(x3, x4), и как составной четырехместный предикат, значения которого определяются четырьмя

предметными переменными x1, x2, x3, x4.

Пример 2.1. Предикат x1>x2 – это двуместный предикат, предметной областью которого могут служить любые множества действительных чисел. Высказывания: 6>5 – истинно, а 7>7 и 3>7 – ложны. Различные подстановки чисел вместо одной переменной дают различные одноместные предикаты: x1>5; x1>0; 7>x2 и.т.д.

В описаниях вычислительных процедур встречаются выражения типа «повторять цикл до тех пор, пока переменные х и у не сов-

25

падут, либо прекратить вычисление цикла после 100 повторений». Если через i обозначить счетчик повторений, то описанное здесь условие описывается выражением (x=y)V(i>100), а указание в целом принимает вид:

«повторять, если x y i 100 ».

Кванторы:

Пусть Р(х) – предикат, определенный на М. Высказывание «для всех х из М Р(х) – истинно» обозначается xP(x) (множество М не входит в обозначение и должно быть ясно из контекста). Знак x называется квантором общности. Высказывание «существует такое х, у, М, что Р(х) истинно» обозначается xP(x). Знак x называется квантором существования.

Переход от Р(х) к xP(x) или к xP(x) называется связыванием переменной х, а также навешиванием квантора на переменную х (или на предикат Р), иногда – квантификацией переменной х. Переменная, на которую навешен квантор называется связанной; несвязанная переменная называется свободной.

Смысл связанных и свободных переменных в предикатных выражениях различен. Свободная переменная – это обычная переменная xεM; выражение Р(х) – переменное высказывание, зависящее от значения х.

Выражение xP(x) не зависит от переменной х и при фиксированных М и Р имеет вполне определенное значение.

Навешивать кванторы можно и на многоместные предикаты и, вообще на любые логические выражения, которые при этом заключаются в скобки.

Выражение, на которое навешивается квантор x или x, называется областью действия квантора; все вхождения переменной х в это выражение являются связанными.

Пример. Пусть Р(х) – предикат «х – четное число». Тогда высказывание xP(x) истинно на любом множестве четных чисел и ложно, если М содержит хотя бы одно нечетное число; высказывание xP(x) истинно на любом множестве, содержащем хотя бы одно четное число и ложно на любом множестве нечетных чисел.

26

2.2. Истинные формулы и эквивалентные соотношения

При логической (истинностной) интерпретации логики предикатов возможны три основные ситуации.

1)Если в области М для формулы F существует такая подстановка констант вместо переменных, что F становится истинным высказыванием, то формула F называется выполнимой.

2)Если формула F выполнима в М при любых подстановках констант, то она называется тождественно истинной в М. Формула, тождественно истинная в любых М, называется тождественно ис-

тинной или общезначимой.

Например: формула x(P(x)Λ P x ) – тождественно истинна.

3) Если формула невыполнима в М, она называется тождественно ложной в М. Если F невыполнима ни в каких М, она называ-

ется тождественно ложной или противоречивой.

Формула x(P(x)Λ P x ) – тождественно ложна.

Формулы называются эквивалентными, если при любых подстановках констант они принимают одинаковые значения. В частности, все тождественно истинные формулы (и все ложные) эквивалентны.

Если формулы F1 и F2 эквивалентны, то формула F1~F2 тождественно истинна.

Как исследовать истинность формул? В случае, если М состоит из конечного числа элементов, то мы рассматривали стандартную процедуру – вычисление формул на наборах значений переменных.

Аналогичная процедура в логике предикатов наталкивается на трудности, связанные с тем, что предметные и предикатные переменные могут иметь бесконечные области определения. Поэтому прямой перебор всех значений невозможен и приходиться использовать различные косвенные приемы.

Пример: xP x ~ xP x

Пусть для некоторого предиката Р и области М левая часть истинна. Тогда не существует aεM, для которого Р(а) истинно; следо-

вательно, для всех а Р(а) – ложно, т.е. P a – истинно, и правая

часть истинна. Если же левая часть ложна, то существует aεM, для которого Р(а) истинно и, следовательно, правая часть ложна.

Аналогично доказывается

27

Пусть левая часть истинна для некоторых P1 и P2. Тогда для любого aεM истинно P1(a) Λ P2(a), поэтому P1(a) и P2(a) одновременно истинны для любых а и, следовательно, xP1(x)V xP2(x) истинно. Если же левая часть ложна, то для некоторого aεM ложно либо P1(a), либо P2(a), а следовательно, ложно либо xP1(x), либо

xP2(x), и правая часть ложна. Аналогично доказывается.

x(P1(x) V P2(x)) ~ xP1(x) V xP2(x).

Если же x и x в этих соотношениях поменять местами, то получатся соотношения, верные лишь в одну сторону:

x(P1(x) Λ P2(x)) → xP1(x) Λ xP2(x)

( xP1(x) V x P2(x)) → x(P1(x) V P2(x)).

В таких случаях говорят, что левая часть – более сильная, чем правая, поскольку она требует для своей истинности выполнения более жестких условий, чем правая.

Приведем без доказательства еще несколько соотношений. x y P(x, y) ~ y x P(x, y)

x y P(x, y) ~ y x P(x, y).

Пусть Y – переменное высказывание или формула, не содер-

Эти соотношения означают, что формулу, не содержащую х, можно выносить за область действия квантора, связывающего х.

28

3. Теория графов

3.1.Основные понятия

Так называемые графы являются наиболее исследованным классом объектов, относящихся к графическим представлениям. Графические представления в узком смысле это описание исследуемой системы, процесса, явления средствами теории графов в виде совокупности двух классов объектов: вершин и соединяющих их ребер. Графы и их составляющие характеризуются определенными свойствами и набором допустимых операций над ними.

Определение. Графом G называется совокупность двух множеств: вершин V и ребер Е, между элементами которых определено отношение инцидентности – каждое ребро еεЕ инцидентно ровно двум вершинам v' и v''εV, которые они соединяют. При этом вершина v' (и v'') и ребро е называют инцидентными друг другу, а вершины v' и v'', являющиеся для ребра е концевыми точками, называют смежными. Часто вместо vεV и еεЕ пишут vεG и еεG.

Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой. В этом случае оно называется направленным или ориентированным или дугой и изображается стрелкой, направленной от вершины, называемой началом к вершине, называемой концом.

Граф, содержащий направленные ребра называется ориенти-

рованным или орграфом, а ненаправленные – неориентированным или н-графом.

Ребра, инцидентные одной и той же паре вершин, называется параллельными или кратными. Граф, содержащий кратные ребра называется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей.

Граф называется конечным, если множество его элементов (вершин и ребер) конечно и пустым, если множество его вершин (а следовательно и ребер) пусто. Граф без петель и кратных ребер называется полным, если каждая пара вершин соединена ребром.

Дополнением графа G называется граф G , имеющий те же вершины, что и G и содержащий только те ребра, которые нужно добавить к графу G, чтобы получить полный граф.

Каждому н-графу канонически соответствует орграф с тем же множеством вершин, в котором каждое ребро заменено двумя

29

ориентированными ребрами, инцидентными тем же вершинам и имеющим противоположные направления.

Локальной степенью (или просто степенью) вершины vεV

н-графа G называют количество ребер ρ(V), инцидентных вершине v. В н-графе сумма степеней всех вершин равна удвоенному числу ребер m графа, т.е. четна (полагается, что в графе с петлями петля дает вклад 2 в степень вершины).

v 2m .

v G

Следовательно, в н-графе число вершин нечетной степени четно.

Для вершин орграфа определяются две локальные степени:

1.ρ1(v) – число ребер, выходящих из v.

2.ρ2(v) – число ребер, входящих из v. Петля дает вклад 1 в обе эти степени.

В орграфе суммы степеней всех вершин ρ1(v) и ρ2(v) равны ко-

личеству ребер m этого графа.

Графы G1 и G2 равны, т.е. G1=G2, если их множества вершин и ребер (выраженных через пары инцидентных им вершин) совпада-

ют: V1=V2 и Е1=Е2.

Граф G считается полностью заданным в строгом смысле, если нумерации его вершин и ребер зафиксированы. Графы, отличающиеся только нумерацией вершин и ребер, называются изоморф-

ными.

Пример 3.1.

30