2117
.pdf
1.4. Характеристики случайной выборки
1.4.1. Классификация численных характеристик выборки. Показатели центра распределения
Для выявления закономерностей распределения результатов наблюдений за исследуемым объектом или явлением необходимо определить ряд числовых показателей, описывающих особенности полученных статистических данных. Все числовые характеристики можно разделить на следующие группы:
–показатели центра распределения: среднее арифметическое, мода, медиана;
–показатели степени вариации: размах, дисперсия, среднее квадратичное отклонение, коэффициент вариации;
–показатели формы распределения: показатели асимметрии и эксцесса, кривые распределения.
Показатели центра распределения определяются следующим образом:
1. Среднее арифметическое (математическое ожидание, выборочное среднее) – величина, определяемая по формуле:
–для вариационного ряда: 1 n
xn i 1xi ,
–для дискретного статистического ряда:
|
1 m |
|
m |
||
x |
|
|
niz(i) |
iz(i) . |
|
n i 1 |
|||||
|
i |
1 |
|||
– для интервального статистического ряда:
|
1 m |
|
m |
||
x |
|
|
ni z(i) |
i z(i) , |
|
n i 1 |
|||||
|
i |
1 |
|||
где z(i) – середина i–го интервала.
11
2. Мода – величина, которая в выборке встречается наиболее часто. Для статистического ряда мода соответствует варианту z(i) с наибольшей частотой, для интервального ряда
вначале необходимо определить модальный интервал, т.е. интервал с наибольшей частотой, а затем определить моду по следующей формуле (в случае равных интервалов):
xmod |
x0 |
L |
|
ns |
ns 1 |
, |
|
(ns |
ns 1) (ns ns 1) |
||||||
|
|
|
|
||||
где x0 – нижняя граница модального интервала, L – величина модального интервала, ns – частота модального интервала, ns 1 и ns 1 – частоты интервалов, расположенных до и после
модального интервала, соответственно.
3. Медиана – величина, которая находится в середине упорядоченного ряда, т.е. первая половина элементов ряда меньше медианы, а вторая – больше ее. Медиана определяется следующим образом:
– для вариационного ряда:
|
x(n 1) / 2 , |
|
если n |
нечетное число, |
|||
x med |
x |
n / 2 |
x |
n / 2 1 |
, |
если n |
четное число, |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
– для дискретного статистического ряда определяются индексы элементов, необходимых для вычисления xmed , а
сами элементы выбираются из соображений принадлежности индексов конкретному значению ряда (по частоте или накопленной частоте);
– для интервального статистического ряда вычисляется номер медианного элемента по формуле
s |
n 1 |
, |
|
2 |
|
||
|
|
|
|
где квадратные скобки показывают, что берется целая часть значения внутри них, определяется интервал, содержащий данный элемент, а само значение медианы находится из соотношения
12
|
|
|
0.5 n |
n нак |
|
x med |
x 0 |
L |
|
s 1 |
, |
n s |
|
||||
|
|
|
|
|
где x0 – нижняя граница медианного интервала, L – величина медианного интервала, ns – частота медианного интервала,
нак |
– накопленная частота интервала, предшествующего |
ns 1 |
медианному.
Основное свойство медианы заключается в том, что
сумма абсолютных отклонений всех элементов выборки от медианы меньше, чем от любого другого значения.
Пример. Определить показатели центра распределения по данным интервального статистического ряда из табл. 3.
Найдем необходимые показатели по формулам для интервального статистического ряда:
– среднее арифметическое: m
xi z(i) 
i1
3.20 |
0.2 |
3.76 |
0.1 |
4.32 |
0.2 |
4.88 |
0.25 |
6.00 |
0.1 |
4.516 |
||||||||||
– мода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xmod |
x0 |
|
L |
|
|
|
|
ns |
|
ns 1 |
|
|
|
|
|
||||
|
|
(ns |
ns 1) (ns |
|
ns 1) |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
4.60 |
0.56 |
|
|
|
5 |
4 |
|
|
|
|
4.79 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(5 |
4) |
(5 |
3) |
|
|
|
|
|
||||||||||
– медиана: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
s |
|
n |
1 |
|
|
|
20 |
1 |
10, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0.5 n |
|
нак |
|
|
|
|
|
|
0.5 20 |
6 |
|
|
|||||
xmed |
x0 |
L |
ns |
1 |
|
|
4.04 |
|
0.56 |
|
4.60 |
|||||||||
|
ns |
|
|
|
|
|
|
|
4 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
13
1.4.2. Показатели степени вариации
Средняя величина дает некую обобщенную характеристику изучаемого объекта или явления. Но для более полного описания необходимо знать степень разбросанности элементов выборки вокруг среднего значения. С этой целью определяются следующие показатели вариации:
1. Вариационный размах (амплитуда колебаний) –
разница между максимальным ( xmax ) и минимальным ( xmin ) элементами выборки:
Rxmax xmin .
2.Выборочная дисперсия представляет собой средний квадрат отклонений значений отдельных элементов выборки от их средней величины:
– для вариационного ряда:
21 n (xi x)2 , n i 1
–для дискретного статистического ряда:
2 |
|
1 m |
x)2 ni |
m |
x)2 |
|
|||
|
|
|
|
(z(i) |
(z(i) |
i , |
|||
|
|
n i |
|||||||
|
|
1 |
|
i 1 |
|
|
|||
– для интервального статистического ряда: |
|||||||||
|
2 |
1 |
m |
x)2 ni |
m |
x)2 |
|
||
|
|
|
|
(zi |
(zi |
i , |
|||
|
|
|
|
|
|||||
|
|
|
n i 1 |
|
i 1 |
|
|
||
3. Выборочное среднее квадратичное отклонение:
2 .
Среднее квадратичное отклонение играет важную роль в анализе статистических данных. Так, для большинства унимодальных распределений выполняется правило трех сигм, согласно которому 99.7% наблюдений принадлежат интервалу
(x 3 , x 3 ) .
4. Коэффициент вариации – применяется для сравнения стандартных отклонений нескольких выборок:
14
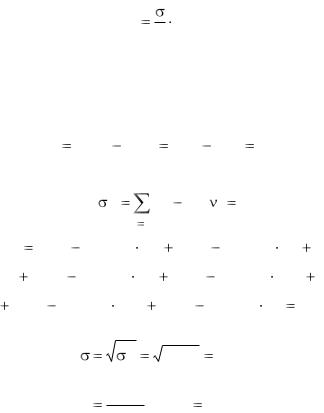
V x 100%
Пример. Определить показатели вариации по данным интервального статистического ряда из табл. 3.
Найдем необходимые показатели по формулам для интервального статистического ряда:
– вариационный размах:
R xmax xmin 6.28 2.92 3.36 ,
– выборочная дисперсия:
|
|
|
2 |
m |
|
x)2 |
|
|
|
|
|
|
|
|
|
(zi |
i |
|
|
|
|||
|
|
|
i |
1 |
|
|
|
|
|
|
|
(3.20 |
4.516)2 |
0.2 |
(3.76 |
4.516)2 |
0.1 |
||||||
(4.32 |
4.516)2 |
0.2 |
(4.88 |
|
4.516)2 |
0.25 |
|||||
(5.44 |
4.516)2 |
0.15 |
(6.00 |
4.516)2 |
0.1 |
0.346 |
|||||
– выборочное среднее квадратичное отклонение:
2 |
0.346 0.589 |
, |
|
– коэффициент вариации:
V0.5894.516 
100% 13.04% .
1.4.3.Показатели формы распределения
Показатели центра распределения и степени вариации не дают никакой информации о форме распределения результатов наблюдений. Для выявления формы используются следующие основные показатели:
1. Квантили (градиенты) – значения, разделяющие элементы выборки на группы определенного объема.
В зависимости от размера групп выделяют следующие квантили:
15
– квартили – значения Q1,Q2 , Q3 , разделяющие элементы выборки на 4 группы одинакового размера; точка Q1
– нижний квартиль – отделяет 1/4 элементов выборки с наименьшими значениями, Q2 – второй (центральный)
квартиль – равен медиане выборки, Q3 – верхний квартиль –
отсекает 1/4 элементов с наибольшими значениями;
– квинтили, децили, процентили – значения,
разделяющие выборку на 5, 10 и 100 частей, соответственно.
2. Моменты распределения используются для более подробного описания формы распределения. Наиболее часто используется центральные моменты k–го порядка,
определяемые по формуле:
1
k n
n |
|
k n . |
x |
x |
|
i |
|
i |
i 1 |
|
|
Моменты распределения имеют важное значение при анализе статистических данных и используются как
самостоятельно (например, |
2 ), так и для определения |
|
2 |
других характеристик.
3. Кривые распределения графически выражают закономерности распределения элементов выборки.
Кривые распределения бывают симметричные и асимметричные. В зависимости от того, какая ветвь кривой вытянута, различают правостороннюю и левостороннюю
асимметрию (рис. 4).
16
а |
б |
Рис. 4. Кривые распределения с левосторонней (а) и правосторонней (б) асимметрией
Для проверки симметричности кривых используются следующие условия и показатели:
1. Условие равенства среднего арифметического значения, моды и медианы:
x xmod xmed .
Если соотношение нарушено, то это свидетельствует о
наличии асимметрии распределения. Так, при xmod |
xmed |
x |
|
асимметрия правосторонняя, а при |
xmod |
xmed |
x |
асимметрия левосторонняя.
2. Условие равенства нулю центрального момента 3–го порядка:
3 0 .
Для характеристики асимметрии используется коэффициент асимметрии, равный отношению центрального момента 3–го порядка к среднему квадратичному отклонению в кубе
1 33 .
17
|
|
|
Для |
симметричных |
распределений |
1 |
|
3 |
0 . |
При |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 0 |
( |
3 |
0 ) |
распределение |
имеет |
левостороннюю |
|||||||||||
асимметрию, при |
1 |
0 ( |
3 0 ) |
– правостороннюю. |
Если |
||||||||||||
|
3 |
0.5 |
, |
то |
асимметрия |
|
считается значительной, |
при |
|||||||||
|
3 |
|
0.25 – незначительной. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Для |
определения островершинности |
симметричного |
||||||||||||
распределения используется коэффициент эксцесса: |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
4 |
|
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
При |
|
нормальном |
распределении |
|
2 |
|
0 , |
при |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
островершинном |
2 |
0 , при плосковершинном |
2 |
|
0 . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1.4.4. Функция |
распределения |
и |
|
плотность |
||||||||||
распределения |
|
|
|
|
|
|
|
|
|
|
|
||||||
Рассмотренные числовые показатели описывают отдельные характеристики распределения значений элементов внутри выборки. Математическими моделями, полностью представляющими зависимости между элементами выборки, являются выборочная функция распределения и выборочная плотность распределения.
Выборочная (эмпирическая) функция распределения
используется, как правило, для описания дискретных рядов небольшого объема и определяется по формуле
F(x) |
n x |
, |
|
n |
|||
|
|
где nx – количество элементов выборки, меньших х. Таким образом, F(x) есть относительная частота появления события A (X x) , заключающегося в том, что случайная величина Х
будет меньше значения х в n независимых испытаниях. Аналитически функция распределения задается
следующим образом:
18
0, |
x |
x1, |
i |
1 |
|
F(x) |
j, xi |
1 x xi , i 2,...,n, |
j |
1 |
|
1, |
x |
x n |
Как видно из формулы, график эмпирической функции распределения имеет ступенчатую форму (рис. 5).
1 |
|
|
|
|
… |
|
|
… |
|
1 |
2 |
|
|
|
1 |
|
|
|
|
0 |
|
… |
|
x |
|
x1 x2 |
x n |
Рис. 5. График эмпирической функции распределения
Выборочная (эмпирическая) плотность распределения
применяется для описания интервального статистического ряда и определяется следующим образом:
p(x) |
ni |
, |
n Li |
||
где Li – длина i–го интервала; |
если длина интервалов |
|
одинакова, то Li L .
Графиком плотности распределения является
нормированная гистограмма относительных частот, которая отличается от ненормированной наличием в знаменателе дроби длины интервала.
19
Точность эмпирической функции распределения и эмпирической плотности распределения возрастает с увеличением объема случайной выборки и при n 
стремится к теоретическим функциональным характеристикам генеральной совокупности.
1.5. Проверка статистических гипотез
Статистическая гипотеза – это предположение о виде или отдельных параметрах распределения значений выборки, которое необходимо проверить.
В зависимости от содержания гипотезы можно разделить на две группы:
–параметрические – содержат утверждения о параметрах генеральной совокупности;
–непараметрические – содержат утверждения обо всем распределении случайной величины.
Процедура проверки гипотезы включает следующие основные этапы:
1. Формулируется основная (нулевая) гипотеза H0 и отрицающая ее альтернативная гипотеза H1 . Как правило, H0 заключается в том, что все значения выборки случайны и никаких взаимосвязей между ними нет, а гипотеза H1
предполагает наличие закономерностей в экспериментальных данных.
2.Принимается уровень значимости гипотезы 
– вероятность ошибочного вывода, когда будет отвергнута
верная гипотеза. Как правило, 
принимает стандартные значения 0.05, 0.01 или 0.005.
3.Выбирается критерий К, позволяющий сравнить выдвинутые гипотезы на предмет их противоречивости выборочным данным.
4. Для гипотезы определяется критическая область – набор значений критерия К, при которых верная гипотеза
20