
Моделирование электропривода. Фролов Ю.М
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
Ю.М. Фролов
МОДЕЛИРОВАНИЕ ЭЛЕКТРОПРИВОДА
Конспект лекций Часть 2
Воронеж 2001
42
УДК 62-83.681.513.3
Фролов Ю.М .Моделирование электроприводов: Конспект лекций (часть 2). Воронеж: Изд-во ВГТУ, 2001. 53 с.
Рассмотрены вопросы составления алгоритмов реализации математических моделей, методы численного интегрирования, изложены основные направления развития программных средств, применительно к моделированию электроприводов приведены специализированные программные средства с рекомендациями по их применению.
Конспект лекций предназначен для студентов специальности 180400 «Электропривод и автоматика промышленных установок и технологических комплексов», изучающих курс «Моделирование электропривода», и может быть использован студентами, обучающи-мися по направлению «Электротехника, электромеханика и электро-технологии».
Конспект лекций подготовлен на магнитном носителе в текстовом редакторе Microsoft Word 98 содержится в файле КОНСП_ЛЕК2_МЭП.rar объемом 548988 байт
Табл. 5 Ил. 20 Библиогр.:10 назв.
Рецензенты: кафедра электротехники Воронежского государственного аграрного университета;
канд. техн. наук Хомяк В.А.
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
©Фролов Ю.М., 2001
© Оформление.Издательство Воронежского государственного технического университета, 2001
43
ВВЕДЕНИЕ
При автоматизированном проектировании электроприводов на этапе технического проекта рассматриваются вопросы, связанные с реализацией ранее принятых технических решений в виде структурных и принципиальных схем и определением их параметров с целью обеспечения условий работоспособности проектируемого электропривода, которые заложены в техническом задании на разработку нового объекта.
Успешное решение указанной задачи возможно только при наличии качественной модели проектируемого компонента. Об этом свидетельствует хотя бы тот факт, что математическое обеспечение, к которому относятся математические методы, математические модели и алгоритмы проектирования, представленные в заданной форме и необходимые для выполнения автоматизированного проектирования, входит в подсистему средств обеспечения системы автоматизированного проектирования (САПР). Особые требования предъявляются к моделям, используемым в САПР, ибо они должны являться информационной основой для решения широкого круга задач проектирования – отображения и документирования информации, анализа объекта проектирования (расчетные задачи, моделирование функционирования объекта) и т.п. Кроме того, среди предметов автоматизации проектирования, помимо формализации проектных процедур, создания структур и типизации процессов проектирования, способов построения технических средств, языков, программ, банков данных, важное место занимают модели, методы и алгоритмы решения проектных задач. В связи с этим, средства моделирования составляющих электропривод элементов образуют основное функциональное ядро современных систем автоматизированного проектирования. Моделирование имеет большое значение не только при автоматизированном проектировании, но и анализе динамических свойств различных структур электроприводов в учебном процессе при подготовке студентов электротехнических специальностей.
Во второй части предлагаемого конспекта лекций даются общие сведения по вопросам составления алгоритмов реализации математических моделей, методам численного интегрирования. В конспекте лекций приведены возможности и целесообразные области применения методов численного интегрирования в практике моделирования. В инструментальных средствах моделирования изложены основные направления развития программных средств, применительно к моделированию электроприводов подробно рассмотрены: программа комплексного анализа структурных схем, система автоматизированного моделирования и параметрической оптимизации, программная система машинного анализа и синтеза систем. Даны рекомендации по их применению при моделировании сложных электротехнических объектов.
44
6. ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
6.1. Алгоритм реализации математической модели
Использование ЭВМ предполагает, что реализуемая задача разделяется на последовательность таких простых функций, которые принципиально выполнимы машиной. Этот процесс называется алгоритмизацией, а его результат алгоритмом.
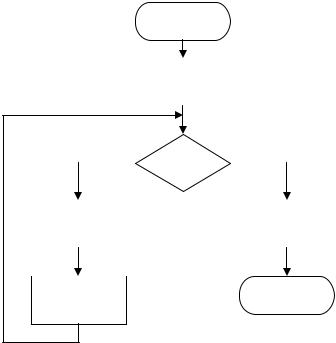
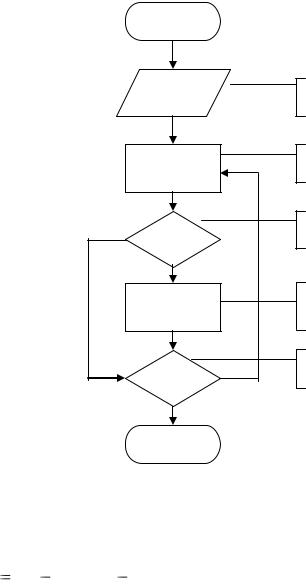
Алгоритмизировать – разложить задачу или еѐ часть в последовательность простых действий. Наиболее распространенным представлением алгоритма программы, позволяющей реализовать математическую модель, является структурная схема (рис.6.1). Из рис.6.1 можно установить взаимосвязь между условными обозначениями на схеме и получающейся для неѐ программой. Действия формируются следующими друг за другом командами операций по обработке, передаче данных и управлению. Условия выполняются командами условного перехода (2) , стрелками указаны команды безусловного перехода. Помимо структурного представления используется представление алгоритма в табличной форме.
|
|
|
НАЧАЛО |
|
|
|
|
|
|
|
|
|
|
|
|
|
ДЕЙСТВИЕ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
НЕТ |
2 |
|
ДА |
|||
|
|
|
УС- |
|
|
|
3 |
|
|
5 |
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
ДЕЙСТВИЕ |
|
|
|
Частичный |
||
2 |
|
|
|
алгоритм |
||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
ДЕЙСТВИЕ |
|
|
КОНЕЦ |
|||
|
|
|
|
|
||
3
Рис.6.1. Структурная схема представления алгоритма
По ходу разработки алгоритма программы он претерпевает уточнение, расшифровку частичного алгоритма с последующей выдачей структурной схемы полного алгоритма.
45

Структурные схемы алгоритмов формируются из следующего набора функциональных элементов – блоков (рис.6.2).
обозначает выполнение операций или группы операций, в результате которых изменяется значение, форма представления или расположение данных (например оператор присваивания);
условный арифметический или логический оператор;
оператор цикла (говорит о выполнении операций, меняющих команды или группы команд, изменяющих программу);
использует ранее созданные и отдельно описанные алгоритмы и программы;
"пуск - останов" для указания начала, окончания процесса обработки данных или выполнения программы;
комментарий, если пояснение не умещается внутри графического символа, помещают на свободном месте и смещают;
соединитель;
межстраничный соединитель;
ручной ввод данных;
преобразования;
документ;
дисплей;
магнитный диск.
Рис.6.2. Функциональные блоки алгоритмов
6.2. Методы численного интегрирования
46
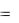
При анализе динамических моделей, в которых взаимосвязь элементов моделируемого объекта в процессе его работы описывается системой дифференциальных, алгебраических и конечно-разностных уравнений, наиболее распространенным способом вычисления фазовых координат модели является численное интегрирование.
Суть любого метода численного интегрирования сводится к тому, что вместо точного решения системы уравнений ищется последовательность приближенных значений координат в дискретные моменты времени. Для этого заданный интервал исследования разбивается на последовательные участки, разделяемые узловыми точками. Расстояние между соседними узловыми точками называется шагом интегрирования. Известно, что количество уравнений, содержащихся в математической модели, определяет затраты времени на каждом шаге интегрирования, а характер интегрируемых функций (скорость их изменения, наличие изломов и т.п.) определяет густоту узловых точек. В общем случае, чем проще модель, тем меньше затраты на моделирование. Однако, в первую очередь, ее выбор определяется адекватностью задачам моделирования, насколько достоверно и точно модель воспроизводит требуемые показатели качества реального объекта.
После того, как математическая модель определена, возникает проблема выбора метода интегрирования, обеспечивающего требуемую точность вычислений при минимуме затрат. Ниже приводятся некоторые рекомендации по выбору различных методов интегрирования применительно к решению задач исследования свойств динамических моделей.
Эффективность использования того или иного метода численного интегрирования может быть оценена как отношение точности результатов, выражаемой через величину максимальной ошибки, к затратам на интегрирование, выражаемое в количестве необходимых вычислений. Самым трудоемким, как правило, является процесс вычисления производных интегрируемых функций, объем которого пропорционален порядку системы дифференциальных уравнений. Поэтому в качестве меры затрат на интегрирование при сравнении различных методов может быть использовано количество обращений к процессу вычисления правых частей. Существенное влияние на производительность метода оказывают характеристики математической модели объекта моделирования. Метод Эйлера является простейшим из большой группы пошаговых методов численного интегрирования, нашедших распространение в практике моделирования.
Дифференциальное уравнение первого порядка, разрешенное относительно производной (представленного в форме Коши)
y f (y, t). |
(6.1) |
|
47 |
|
Правая часть равенства представляет собой выражение, по которому при |
любом |
значении y(t) можно вычислить производную некоторой функции |
y(y, t) |
в произвольный момент времени t n . Существует множество решений |
y(t) , удовлетворяющих уравнению (6.1) и каждое из них определяется заданными начальными условиями (y0 , t0 ) , то есть исходной точкой на плоскости y, t (рис.6.3).
В каждой точке интегрирования по выражению (6.1) определяется значение производной интегрирования функции y(t) , геометрическим образом
которой на рис.6.3 служит касательная к искомой кривой, и по формуле Эйлера
y(t0 1 ) y(t0 ) |
hy(t0 ) |
(6.2) |
|
вычисляется |
значение интегрируемой функции в точке t1 t0 h . |
С |
|
помощью полученного значения y(t1 ) |
можно определить производную y(t1 ) |
и |
|
повторить процесс вычисления искомой функции в точке t 2 . Интегрирование
продолжается до тех пор, пока не будет исчерпан весь заданный временной диапазон (t0 , t k ) .
Y
Yуст
Y1
y(t0 h)
Yуточн
y(t 0 )
Y0
t0 |
t0+h |
t0+2h |
t |
Рис.6.3. Графическая интерпретация метода Эйлера
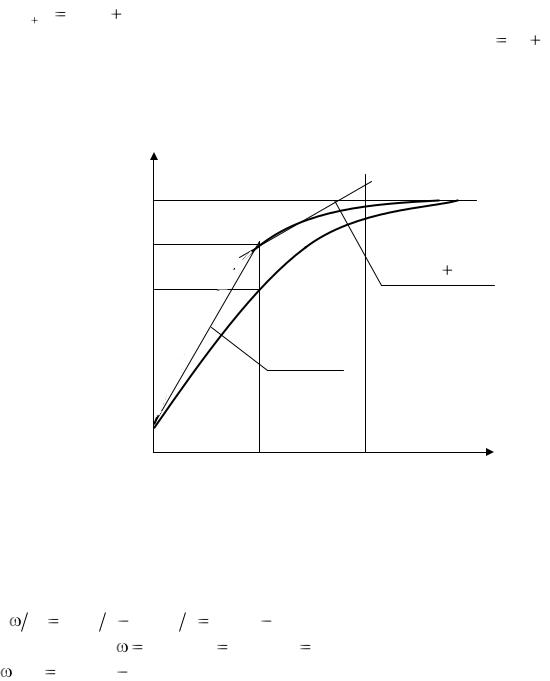
Например, при пуске двигателя постоянного тока независимого возбуждения в одномассовой электромеханической системе (рис.6.4) уравнение движения электропривода
d dt |
M(t) J |
Mc (t) J aM(t) b . |
При t 0 |
имеем |
0, M(t0 ) Mk , Mc const . |
(t0 ) |
aM(t0 ) |
b . |
48
Тогда скорость при t1 будет равна: (t1) 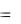 (t0 )
(t0 ) 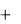 (t0 )h .
(t0 )h .
За шаг интегрирования угловая скорость увеличивается от 0 до (t1 ) ,
которой по механической характеристике будет соответствовать другой момент M(t1 ) , определяющий значение ускорения на втором шаге интегрирования:
(t1 ) aM(t1 )
y(t1 )
y(t 0 )
b . |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
c |
|
|
|
|
|
|
(t 2 ) |
|
|
|
|
|
|
(t1 ) |
|
|
|
|
|
|
(t0 ) |
h |
h |
|
|
M |
|
t0 |
|
Mc |
M(t2) M(t1) |
M(t0) |
tk |
t |
Рис.6.4. Механическая характеристика электродвигателя
Угловая скорость двигателя в конце второго шага будет равна
(t2 ) 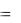 (t1 )
(t1 ) 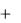 (t1)h .
(t1)h .
Этой скорости соответствует момент двигателя M(t 2 ) , который
определит ускорение на третьем шаге интегрирования. Процесс будет продолжаться, пока соблюдается условие ti tk .
Анализируя формулу интегрирования (6.2), нетрудно убедиться, что решение определяется с некоторой ошибкой, поскольку на отрезке t0 t0 h
на шаге интегрирования действительное значение изменяющейся функции y(t) заменяется отрезком прямой (dy dt)h .
dt)h .
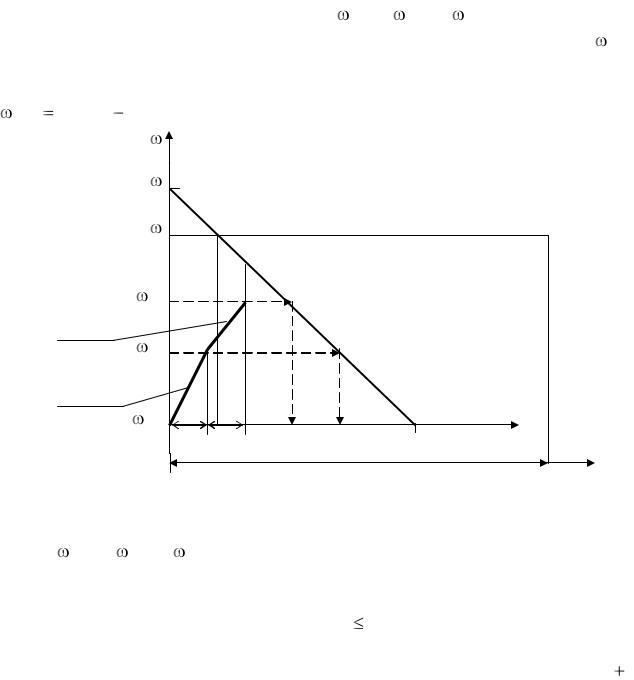
Алгоритм решения (рис.6.5) охватывает следующую последовательность действий. Исходным пунктом является задание исходных данных моделирования: начального t 0 и конечного t k значений независимой
переменной, величины шага интегрирования h , исходных значений интегрируемых переменных и параметров дифференциальных уравнений. На начальном этапе независимой переменной t присваивается исходное значение t 0 .
49
НАЧАЛО
Задание исходных данных
Вычисление фазовых координат
Нет |
Фиксировать результаты |
Вывод результатов моделирования
Окончить
Нет
Да
КОНЕЦ
Рис.6.5. Алгоритм решения по методу Эйлера
Величина интервала h определяется исходя из потребного количества точек индикации результатов N n согласно равенству (6.3).
h (t k t0 ) /(Nn 1) . |
(6.3) |
Следующим этапом является вычисление фазовых координат по формулам (6.1), (6.2). Рис.6.4 иллюстрирует решение одного уравнения первого порядка, однако алгоритм не претерпевает изменений при решении системы дифференциальных уравнений. В этом случае вычисления производных и интегрируемых функций повторяются для каждой фазовой координаты математической модели по числу дифференциальных уравнений.
Реализация алгоритма (рис.6.5) требует некоторой подготовительной работы, вызванной спецификой метода вычислений и особенностями работы ЭВМ. Применение методов численного интегрирования требует приведения уравнений моделируемой системы к форме Коши. Применительно к дифференциальным уравнениям высоких порядков это означает, что при введении вспомогательных переменных они должны быть преобразованы в систему уравнений первого порядка. Например, уравнение
50

|
dn y |
|
a1 |
dn 1y |
|
|
a n 1 |
dy |
|
a n y f (t) , |
|
|
|
|
||
|
dtn |
dtn 1 |
|
dt |
|
|
|
|
|
|||||||
введением вспомогательных переменных |
|
|
|
|
||||||||||||
dy dt y ; d2 y dt2 |
dy dt y |
2 |
; ; dn 1y dt n 1 |
dy |
n 2 |
dt y |
n 1 |
|||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||||
приводится к виду: |
|
|
|
|
|
|
|
|
|
|
||||||
dy dt y1;dy1 dt y2 ;dy2 dt y3 ; ;dyn 2 dt yn 1; |
|
|
|
|||||||||||||
dyn 1 |
dt f (t) |
a1yn 1 a 2 yn |
2 a n 2 y2 a n 1y1 |
a n y. |
|
|||||||||||
Использование ЭВМ в качестве инструмента исследования предопределяет необходимость оформить алгоритм вычислений в форме программы, написанной на алгоритмических языке высокого уровня.
Дальнейшим этапом реализации алгоритма построения переходного процесса является отладка программы.
Помимо метода Эйлера, простейшего из большой группы пошаговых методов численного интегрирования, известны методы Рунге-Кутта различных порядков, алгоритм которых описывается выражением
|
p |
|
yn 1 yn |
i ki , |
(6.4) |
|
i 1 |
|
где p – порядок дифференциального уравнения, i – номер коэффициента пропорциональности. Коэффициенты ki имеют вид:
|
|
k1 |
h f (yn , t n ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
k 2 |
h f (yn |
21k1, t n |
2 h); |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
; |
|
|
|
|
|
|
(6.5) |
|
|
|
|
|
|
|||||
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ki |
h f (yn |
i, jk j |
, t n |
i h); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
j |
– |
номер |
коэффициента |
|
в уравнении |
|
коэффициента |
||||||||||
пропорциональности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Как частные случаи из этих выражений могут быть получены формулы |
||||||||||||||||||
Эйлера |
(p |
1, |
1) , |
улучшенного метода Эйлера |
(p |
2, |
1 |
|
2 |
1, |
12 |
1, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
1) ; классического метода Рунге-Кутта (p |
4, |
1 |
4 |
1/ 6, |
2 |
3 |
2 / 6, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
21 |
|
32 |
1/ 2, |
31 |
41 |
42 |
0, |
43 |
1, |
2 |
3 |
1/ 2, |
4 |
1) и др. |
Тогда |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
формула Эйлера представляет частный случай формулы Рунге-Кутта и принимает следующий вид:
yn 1 |
yn 1k1 |
yn |
h f (yn , tn ) |
yn |
h y(tn ). |
|||
Формула Рунге-Кутта четвертого порядка |
|
|||||||
|
p |
4 |
|
|
|
|
|
|
yn 1 |
yn |
|
i ki |
yn |
1k1 |
2 k 2 |
3k3 |
4 k 4 |
|
i |
1 |
|
|
|
|
|
|
yn |
(1/ 6)(k1 |
2k2 |
2k3 k4 ) , |
|
|
|||
51
